
2008年广东省茂名市初中毕业生学业考试与高中阶段学校招生考试
数学试卷
第一卷(选择题,满分40分,共2页)
一、精心选一选(本大题共10小题,每小题4分,共40分.每小题给出四个答案,其中只有一个是正确的).
1.-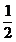 的相反数是( )
的相反数是( )
A.-2
B.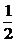 D.
D.
2.下列图形中,既是轴对称图形又是中心对称图形的是( )
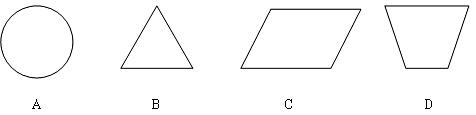
3.下列运算正确的是( )
A.-2 =4
B.2
=4
B.2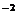 =-4
=-4
C.  ?
?
 =
= 
 D.
D. +2
+2 =3
=3
4.用平面去截下列几何体,截面的形状不可能是圆的几何体是( )
A.球 B.圆锥 C.圆柱 D.正方体
5.任意给定一个非零数,按下列程序计算,最后输出的结果是( )

A. B.
B. C.
C. +1
D.
+1
D. -1
-1
6.在数轴上表示不等式组 的解集,正确的是( )
的解集,正确的是( )

A B

C D
7.正方形内有一点A,到各边的距离从小到大依次是1、2、3、4,则正方形的周长是( )
A.10
B.
8.一组数据3、4、5、 、7的平均数是5,则它的方差是( )
、7的平均数是5,则它的方差是( )
A.10
B.
9.已知反比例函数 =
=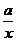 (
( ≠0)的图象,在每一象限内,
≠0)的图象,在每一象限内, 的值随
的值随 值的增大而减少,则一次函数
值的增大而减少,则一次函数 =-
=-
 +
+ 的图象不经过( )
的图象不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
10.如图,△ABC是等边三角形,被一平行于BC的矩形所截,AB被截成三等分,则图中阴影部分的面积是△ABC的面积的 ( )
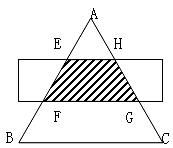
A. B.
B. C.
C. D.
D.
第二卷(非选择题,共8页,满分110分)
二、耐心填一填(本大题共5小题,每小题4分,共20分.请你把答案填在横线的上方).
11.据最新统计,茂名市户籍人口约为7020000人,用科学记数法表示是 人.
12.分解因式:3
 -27= .
-27= .
13.如图,点A、B、C在⊙O上,AO∥BC,∠AOB = 50°, 则∠OAC的度数是 .
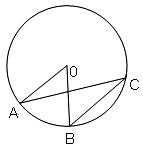
14.依法纳税是每个公民应尽的义务,新的《中华人民共和国个人所得税法》规定,从

15.有一个运算程序,可以使: ?
? =
= 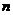 (
(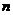 为常数)时,得(
为常数)时,得( +1)?
+1)? =
= 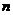 +1,
+1,  ?(
?( +1)=
+1)= 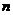 -2现在已知1?1 =
2,那么2008?2008 =
.
-2现在已知1?1 =
2,那么2008?2008 =
.
三、细心做一做 (本大题共3小题,每小题8分,共24分)
16.(本题满分8分)计算:(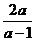 -
- 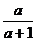 )?
)? 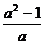
17.(本题满分8分)如图,方格纸中有一条美丽可爱的小金鱼.
(1)在同一方格纸中,画出将小金鱼图案绕原点O旋转180°后得到的图案;(4分)
(2)在同一方格纸中,并在 轴的右侧,将原小金鱼图案以原点O为位似中心放大,使它们的位似比为1:2,画出放大后小金鱼的图案.(4分)
轴的右侧,将原小金鱼图案以原点O为位似中心放大,使它们的位似比为1:2,画出放大后小金鱼的图案.(4分)

18.(本题满分8分)不透明的口袋里装有3个球,这3个球分别标有数字1、2、3,这些球除了数字以外都相同.
(1)如果从袋中任意摸出一个球,那么摸到标有数字是2的球的概率是多少?(2分)
(2)小明和小东玩摸球游戏,游戏规则如下:先由小明随机摸出一个球,记下球的数字后放回,搅匀后再由小东随机摸出一个球,记下球的数字.谁摸出的球的数字大,谁获胜.现请你利用树状图或列表的方法分析游戏规则对双方是否公平?并说明理由.(6分)
四、沉着冷静,周密考虑(本大题共2小题,每小题8分,共16分)
19.(本题满分8分)
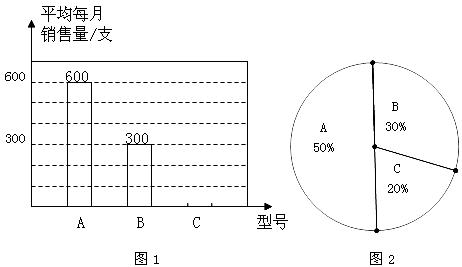
20.(本题满分8分)某文具店王经理统计了2008年1月至5月A、B、C这三种型号的钢笔平均每月的销售量,并绘制图1(不完整),销售这三种型号钢笔平均每月获得的总利润为600元,每种型号钢笔获得的利润分布情况如图2.已知A、B、C这三种型号钢笔每支的利润分别是0.5元、0.6元、1.2元,请你结合图中的信息,解答下列问题:
(1)求出C种型号钢笔平均每月的销售量,并将图1补充完整;(4分)
(2)王经理计划6月份购进A、B、C这三种型号钢笔共900支,请你结合1月至5月平均
每月的销售情况(不考虑其它因素),设计一个方案,使获得的利润最大,并说明理由.(4分)
五、开动脑筋,再接再厉 (本大题共3小题,每小题10分,共30分)
21.(本题满分10分)
如图,某学习小组为了测量河对岸塔AB的高度,在塔底部B的正对岸点C处,测得仰角∠ACB=30°.
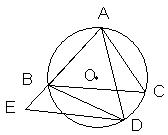
(1)若河宽BC是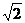 ≈1.414,
≈1.414,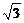 ≈1.732)
≈1.732)
(2)若河宽BC的长度无法度量,如何测量塔AB的高度呢?小明想出了另外一种方法:从点C出发,沿河岸CD的方向(点B、C、D在同一平面内,且CD⊥BC)走 米,到达D处,测得∠BDC=60°,这样就可以求得塔AB的高度了.请你用这种方法求出塔AB的高.(6分)
米,到达D处,测得∠BDC=60°,这样就可以求得塔AB的高度了.请你用这种方法求出塔AB的高.(6分)
22.(本题满分10分)
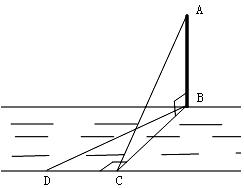
如图,⊙O是△ABC的外接圆,且AB=AC,点D在弧BC上运动,过点D作DE∥BC,DE交AB的延长线于点E,连结AD、BD.
(1)求证:∠ADB=∠E;(3分)
(2)当点D运动到什么位置时,DE是⊙O的切线?请说明理由.(3分)
(3)当AB=5,BC=6时,求⊙O的半径.(4分)
23.(本题满分10分)
如图,在等腰梯形ABCD中,已知AD∥BC,AB=DC,AD=2,BC=4,延长BC到E,使CE=AD.
(1)写出图中所有与△DCE全等的三角形,并选择其中一对说明全等的理由;(5分)
(2)探究当等腰梯形ABCD的高DF是多少时,对角线AC与BD互相垂直?请回答并说明理由.(5分)

|