1．一个正方体的面共有（    ）

A．1个               B．2个              C．4个            D．6个

2．数据1，1，2，2，3，3，3的极差是（    ）

A．1                 B．2                 C．3              D．6

3．的绝对值是（    ）

A．3                 B．              C．          　  D．

4．一个正方形的对称轴共有（    ）

A．1条              B．2条              C．4条             D．无数条

5．若，则的值是（    ）

A．3                 B．              C．0            　 D．6

6．如图1，AB是⊙O的直径，∠ABC=30°,则∠BAC =（    ）

A．90°              B．60°             C．45°            D．30°

7．如图，箭头表示投影线的方向，则图中圆柱体的正投影是（    ）

A．圆        　    B．圆柱             C．梯形         　  D．矩形

8．下列式子正确的是（    ）

A．>0         B．≥0           C．a+1>1           D．a?1>1

9．在直角坐标系中，将点P（3，6）向左平移4个单位长度，再向下平移8个单位长度后，得到的点位于（    ）

A．第一象限      B．第二象限        C．第三象限        　D．第四象限

10．从n张互不相同的普通扑克牌中任意抽取一张，抽到黑桃K的概率为，则n =（    ）

A．54            B．52               C．10               D．5

11．因式分解： =      .

12．如图，P是∠AOB的角平分线上的一点，PC⊥OA于点C，PD⊥OB于点D，写出图中一对相等的线段（只需写出一对即可）     .

13．圆的半径为3cm，它的内接正三角形的边长为     .

14．边长为５cm的菱形，一条对角线长是6cm，则另一条对角线的长是      .

15．已知，，=8，=16，2=32，……观察上面规律，试猜想的末位数是      .

16.（本小题满分6分）

计算：.

17.（本小题满分6分）

在Rt△ABC中，∠C = 90°，a =3 ，c =5，求sinA和tanA的值.

18.（本小题满分6分）　

    解不等式：≥70.

19.（本小题满分7分）

如图， E、F、G分别是等边△ABC的边AB、BC、AC的中点.

（1） 图中有多少个三角形？

（2） 指出图中一对全等三角形，并给出证明.

20.（本小题满分7分）

在四川省发生地震后，成都运往汶川灾区的物资须从西线或南线运输，西线的路程约800千米，南线的路程约80千米，走南线的车队在西线车队出发18小时后立刻启程，结果两车队同时到达．已知两车队的行驶速度相同，求车队走西线所用的时间.

21.（本小题满分7分）

如图，在等腰Rt△ABC中，∠C=90°，正方形DEFG的顶点D在边AC上，点E、F在边AB上，点G在边BC上.

（1）求证AE=BF；

（2）若BC=cm，求正方形DEFG的边长.

22.（本小题满分8分）

已知点A（2，6）、B（3，4）在某个反比例函数的图象上.

（1） 求此反比例函数的解析式；

    （2）若直线与线段AB相交，求m的取值范围.

23.（本小题满分８分）

在2008北京奥林匹克运动会的射击项目选拔赛中，甲、乙两名运动员的射击成绩如下（单位：环）：

甲　10   10.1   9.6   9.8    10.2   8.8    10.4   9.8     10.1   9.2

乙　9.7   10.1   10   9.9    8.9    9.6    9.6    10.3    10.2   9.7

（１）   两名运动员射击成绩的平均数分别是多少?

（２）   哪位运动员的发挥比较稳定？

（参考数据： 0.2=2.14 ，

=1.46）

24.（本小题满分10分）

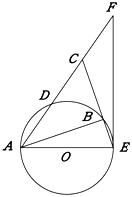
如图，在Rt△ABC中，∠ABC=90°，D是AC的中点，⊙O经过A、B、D三点，CB的延长线交⊙O于点E.

(1)    求证AE=CE；

(2)    EF与⊙O相切于点E，交AC的延长线于点F，若CD=CF=2cm，求⊙O的直径；

   （3）若 （n>0），求sin∠CAB.

25.（本小题满分10分）

已知点A（a，）、B（2a，y）、C（3a，y）都在抛物线上.

（1）求抛物线与x轴的交点坐标；

（2）当a=1时，求△ABC的面积；

（3）是否存在含有、y、y，且与a无关的等式？如果存在，试给出一个，并加以证明；如果不存在，说明理由.