
2008年浙江省绍兴市初中毕业生学业考试
数学试卷
试卷Ⅰ(选择题,共40分)
一、选择题(本大题有10小题,每小题4分,共40分.请选出每小题中一个符合题意的正确选项,不选、多选、错选,均不给分)
1.下列计算结果等于1的是( )
A.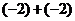 B.
B.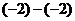 C.
C.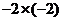 D.
D.
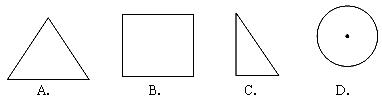
2.下列各图中,为轴对称图形的是( )
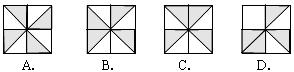
3.如图,沿虚线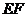 将
将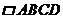 剪开,则得到的四边形
剪开,则得到的四边形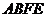 是( )
是( )
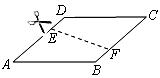
A.梯形 B.平行四边形 C.矩形 D.菱形
4.在一次射击测试中,甲、乙、丙、丁的平均环数均相同,而方差分别为8.7,6.5,9.1,7.7,则这四人中,射击成绩最稳定的是( )
A.甲 B.乙 C.丙 D.丁
5.将如图所示的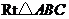 绕直角边
绕直角边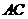 旋转一周,所得几何体的主视图是( )
旋转一周,所得几何体的主视图是( )
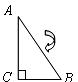
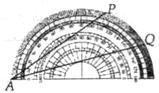
6.如图,量角器外缘边上有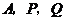 三点,它们所表示的读数分别是
三点,它们所表示的读数分别是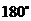 ,
,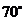 ,
,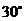 ,则
,则 的大小为( )
的大小为( )
A.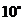 B.
B.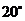 C.
C.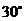 D.
D.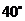
7.已知点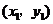 ,
,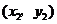 均在抛物线
均在抛物线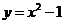 上,下列说法中正确的是( )
上,下列说法中正确的是( )
A.若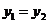 ,则
,则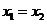 B.若
B.若 ,则
,则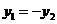
C.若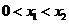 ,则
,则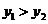 D.若
D.若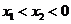 ,则
,则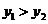
8.将一张纸第一次翻折,折痕为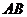 (如图1),第二次翻折,折痕为
(如图1),第二次翻折,折痕为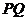 (如图2),第三次翻折使
(如图2),第三次翻折使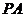 与
与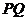 重合,折痕为
重合,折痕为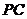 (如图3),第四次翻折使
(如图3),第四次翻折使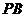 与
与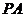 重合,折痕为
重合,折痕为 (如图4).此时,如果将纸复原到图1的形状,则
(如图4).此时,如果将纸复原到图1的形状,则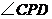 的大小是( )
的大小是( )

A.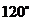 B.
B.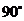 C.
C.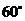 D.
D.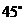
9.兴趣小组的同学要测量树的高度.在阳光下,一名同学测得一根长为
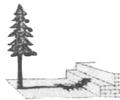
A.
10.本学期实验中学组织开展课外兴趣活动,各活动小班根据实际情况确定了计划组班人数,并发动学生自愿报名,报名人数与计划人数的前5位情况如下:
小班名称
奥数
写作
舞蹈
篮球
航模
报名人数
215
201
154
76
65
小班名称
奥数
舞蹈
写作
合唱
书法
计划人数
120
100
90
80
70
若用同一小班的报名人数与计划人数的比值大小来衡量进入该班的难易程度,则由表中数据,可预测( )
A.奥数比书法容易 B.合唱比篮球容易
C.写作比舞蹈容易 D.航模比书法容易
卷Ⅱ(非选择题,共110分)
二、填空题(本大题有6小题,每小题5分,共30分.将答案填在题中横线上)
11.北京奥运会国家体育场“鸟巢”的建筑面积为258000平方米,那么258000用科学记数法可表示为 .

12.分解因式 .
.
13.如图,已知函数 和
和 的图象交点为
的图象交点为 ,则不等式
,则不等式 的解集为
.
的解集为
.

14.若买2支圆珠笔、1本日记本需4元;买1支圆珠笔、2本日记本需5元,则买4支圆珠笔、4本日记本需 元.
15.如图,轮椅车的大小两车轮(在同一平面上)与地面的触点 间距离为
间距离为

16.如图中的圆均为等圆,且相邻两圆外切,圆心连线构成正三角形,记各阴影部分面积从左到右依次为 ,
, ,
, ,…,
,…, ,则
,则 的值等于
.
的值等于
.

三、解答题(本大题有8小题,第17~20小题每小题8分,第21小题10分,第22,23小题每小题12分,第24小题14分,共80分.解答需写出必要的文字说明、演算步骤或证明过程)
17.(1)计算: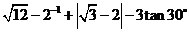 ;
;
(2)解方程: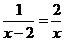 .
.
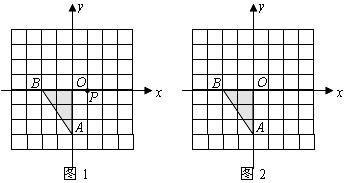
18.在平面直角坐标系中,已知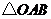 ,
,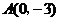 ,
,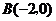 .
.
(1)将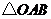 关于点
关于点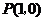 对称,在图1中画出对称后的图形,并涂黑;
对称,在图1中画出对称后的图形,并涂黑;
(2)将 先向右平移3个单位,再向上平移2个单位,在图2中画出平移后的图形,并涂黑.
先向右平移3个单位,再向上平移2个单位,在图2中画出平移后的图形,并涂黑.
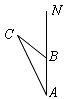
19.地震发生后,一支专业搜救队驱车前往灾区救援.如图,汽车在一条南北走向的公路上向北行驶,当在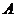 处时,车载GPS(全球卫星定位系统)显示村庄
处时,车载GPS(全球卫星定位系统)显示村庄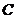 在北偏西
在北偏西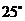 方向,汽车以
方向,汽车以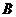 处,GPS显示村庄
处,GPS显示村庄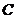 在北偏西
在北偏西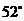 方向.
方向.
(1)求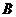 处到村庄
处到村庄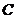 的距离;
的距离;
(2)求村庄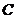 到该公路的距离.(结果精确到
到该公路的距离.(结果精确到
(参考数据: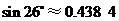 ,
,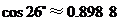 ,
,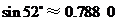 ,
,
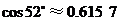 )
)
20.开学前,小明去商场买书包,商场在搞促销活动,买一只书包可以送2支笔和1本书.
(1)若有3支不同笔可供选择,其中黑色2支,红色1支,试用树状图表示小明依次抽取2支笔的所有可能情况,并求出抽取的2支笔均是黑色的概率;
(2)若有6本不同书可供选择,要在其中抽1本,请你帮助小明设计一种用替代物模拟抽书的方法.
21.在城关中学开展的“我为四川地震灾区献爱心”捐书活动中,校团委为了了解九年级同学的捐书情况,用简单的随机抽样方法从九年级的10个班中抽取50名同学,对这50名同学所捐的书进行分类统计后,绘制了如下统计表:
捐书情况统计表
种类
文学类
科普类
学辅类
体育类
其它
合计
册数
120
180
140
80
40
560
(1)在下图中,补全这50名同学捐书情况的频数分布直方图;
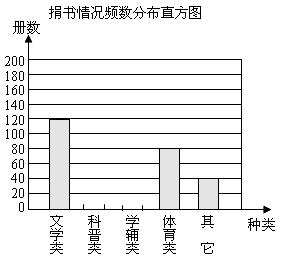
(2)若九年级共有475名同学,请你估计九年级同学的捐书总册数及学辅类书的册数.
22.定义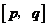 为一次函数
为一次函数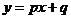 的特征数.
的特征数.
(1)若特征数是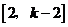 的一次函数为正比例函数,求
的一次函数为正比例函数,求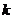 的值;
的值;
(2)设点 分别为抛物线
分别为抛物线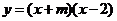 与
与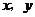 轴的交点,其中
轴的交点,其中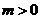 ,且
,且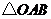 的面积为4,
的面积为4,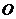 为原点,求图象过
为原点,求图象过 两点的一次函数的特征数.
两点的一次函数的特征数.
23.学完“几何的回顾”一章后,老师布置了一道思考题:
如图,点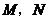 分别在正三角形
分别在正三角形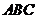 的
的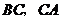 边上,且
边上,且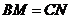 ,
,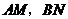 交于点
交于点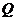 .求证:
.求证: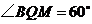 .
.
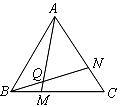
(1)请你完成这道思考题;
(2)做完(1)后,同学们在老师的启发下进行了反思,提出了许多问题,如:
①若将题中“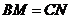 ”与“
”与“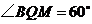 ”的位置交换,得到的是否仍是真命题?
”的位置交换,得到的是否仍是真命题?
②若将题中的点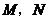 分别移动到
分别移动到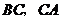 的延长线上,是否仍能得到
的延长线上,是否仍能得到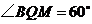 ?
?
③若将题中的条件“点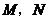 分别在正三角形
分别在正三角形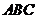 的
的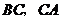 边上”改为“点
边上”改为“点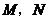 分别在正方形
分别在正方形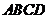 的
的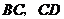 边上”,是否仍能得到
边上”,是否仍能得到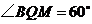 ?……
?……
请你作出判断,在下列横线上填写“是”或“否”:① ;② ;③ .并对②,③的判断,选择一个给出证明.
24.将一矩形纸片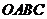 放在平面直角坐标系中,
放在平面直角坐标系中,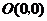 ,
,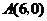 ,
,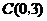 .动点
.动点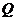 从点
从点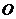 出发以每秒1个单位长的速度沿
出发以每秒1个单位长的速度沿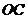 向终点
向终点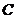 运动,运动
运动,运动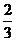 秒时,动点
秒时,动点 从点
从点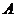 出发以相等的速度沿
出发以相等的速度沿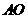 向终点
向终点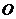 运动.当其中一点到达终点时,另一点也停止运动.设点
运动.当其中一点到达终点时,另一点也停止运动.设点 的运动时间为
的运动时间为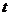 (秒).
(秒).
(1)用含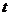 的代数式表示
的代数式表示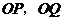 ;
;
(2)当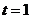 时,如图1,将
时,如图1,将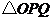 沿
沿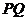 翻折,点
翻折,点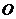 恰好落在
恰好落在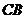 边上的点
边上的点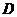 处,求点
处,求点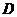 的坐标;
的坐标;
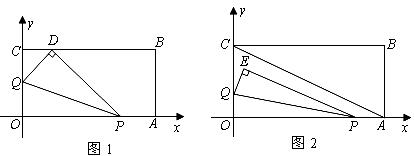
(3)连结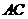 ,将
,将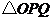 沿
沿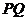 翻折,得到
翻折,得到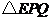 ,如图2.问:
,如图2.问: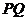 与
与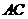 能否平行?
能否平行?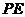 与
与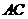 能否垂直?若能,求出相应的
能否垂直?若能,求出相应的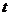 值;若不能,说明理由.
值;若不能,说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com