
2007-2008学年度微山县第一学期九年级期末考试
数学试题
(时间:120分钟 满分:120分)
注意事项:
1.本试题分第Ⅰ卷和第Ⅱ卷两部分,共11页.第Ⅰ卷第1页至第3页为选择题,36分;第Ⅱ卷第4页至第11页为非选择题,84分;共120分。考试时间为120分钟。
2.答卷前务必将自己的姓名、考号等填写在装订线内规定位置。
第Ⅰ卷 (选择题 共36分)
一、选择题(本大题共12小题,每小题3分,共36分。在每小题给出的四个选项中,只有一个是正确的。每小题选对得3分,选错、不选或多选,均不得分,并把答案填写在卷Ⅱ的答题栏内。)
1.当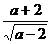 有意义时,
有意义时,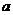 的取值范围是
的取值范围是
A.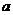 ≥2 B.
≥2 B.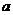 >
>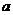 ≠2 D.
≠2 D.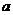 ≠?2
≠?2
2.在Rt△ABC中,∠C=90º,∠A、∠B及∠C所对的边分别为a、b、c,则下列各式中错误的是
A.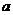 =
= B.
B.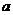 =
=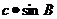
C.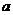 =
=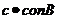 D.
D.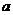 =
=
3.一元二次方程 的根的情况是
的根的情况是
A.方程有两个不相等的实数根 B.方程有两个相等的实数根
C.方程没有实数根 D.方程的根的情况与k的取值有关
4.现有2008年奥运会福娃卡片20张,其中贝贝6张,京京5张,欢欢4张,迎迎3张,妮妮2张,每张卡片大小、质地均匀相同,将画有福娃的一面朝下反扣在桌子上,从中随机抽取一张,抽到京京的概率是
A. B.
B. 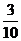 C.
C. 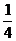 D.
D. 
5.下列两个图形:①两个等腰三角形;②两个直角三角形;③两个正方形;④两个矩形;⑤两个菱形;⑥两个正五边形。其中一定相似的有
A.2组 B.3组 C.4组 D.5组
6.如图1,E是正方形ABCD的边BC上一点,下列条件中:①∠BAE=∠CEF;②∠AEB=∠EFC;③AE⊥EF;④ ;⑤
;⑤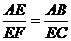 。其中能使△ABE∽△ECF的有
。其中能使△ABE∽△ECF的有
A.①② B.①②③ C.①②③④ D.①②③④⑤
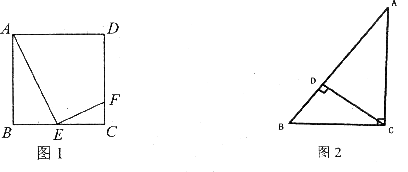
7.如图2,CD是Rt△ABC斜边上的高,则图中相似三角形的对数有
A.0对 B.1对 C.2对 D.3对
8.已知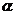 是锐角,
是锐角, ,则
,则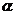 等于
等于
A.30º B.45º C.60º D.90º
9.小明从图3的二次函数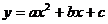 图像中,观察得出了下面的五条信息:①
图像中,观察得出了下面的五条信息:①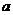 <0②
<0② =0 ③函数的最小值为?3 ④当
=0 ③函数的最小值为?3 ④当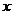 <0时,
<0时, >0 ⑤当0<
>0 ⑤当0<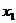 <
< <2时,
<2时,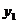 >
>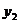 。你认为其中正确的有几个。
。你认为其中正确的有几个。
A.2 B.3 C.4 D.5


10.小明在某次投篮中,球的运动路线是抛物线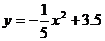 的一部分(如图4),若命中篮圈中心,则他与篮底的距离
的一部分(如图4),若命中篮圈中心,则他与篮底的距离 是
是
A.
11.“圆材埋壁”是我国古代著名数学著作《九章算术》中的问题:“今有圆材,埋在壁中,不知大小从锯锯之,深1寸,锯道长1尺,问径几何?”用数学语言可表述为:如图5,CD 是⊙O的直径,弦AB⊥CD于E,CE=1寸,AB=10寸,则直径CD的长为
A.12.5寸 B.13寸 C.25寸 D.26寸

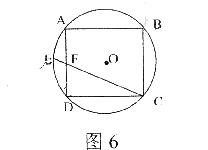
12.如图6,⊙O是正方形ABCD的外接圆,F是AD的中点,CF的延长线交⊙O于E,那么CF┱EF的值是
A.3┱1 8. 4┱l C.5┱1 D.6┱1
第Ⅱ卷 (非选择题,共84分)
二、填空题(本大题共6小题,每小题3分,共18分,只要求填出最后结果。)
13.如果关于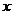 的方程
的方程 有两个相等的实数根,那么实数
有两个相等的实数根,那么实数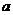 = 。
= 。
14.若抛物线 的顶点为A,与
的顶点为A,与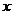 轴的交点为B、C,则△ABC的面积是 。
轴的交点为B、C,则△ABC的面积是 。
15.将抛物线 先沿
先沿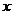 轴方向向左平移2个单位,再沿
轴方向向左平移2个单位,再沿 轴方向向下平移3个单位,所得抛物线的解析式是 。
轴方向向下平移3个单位,所得抛物线的解析式是 。
16.线段AB,CD在平面直角坐标系中位置如图7所示,O为坐标原点。若线段AB上一点 的坐标为(
的坐标为(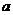 ,
, ),则直线OP与线段CD的交点坐标为 。
),则直线OP与线段CD的交点坐标为 。


17.如图8,在菱形ABCD中,DE⊥AB,垂足是E,DE=6,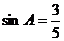 ,则菱形ABCD的周长是 。
,则菱形ABCD的周长是 。
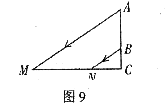
18.如图9,是一束平行的光线从教室窗户射入教室的示意图,测得光线与地面所成的角∠AMC=30º,窗户的高在教室地面上的影长 米,窗户的下檐到教室地面的距离
米,窗户的下檐到教室地面的距离 米(点M、N、C在同一直线上),则窗户的高AB为 。
米(点M、N、C在同一直线上),则窗户的高AB为 。
三、解答题(共66分,解答应写出文字说明、证明过程或推演步骤)
19.解答下列各题(本题满分8分)
(1)计算: +
+ -
-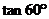 +
+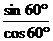
(2)计算:
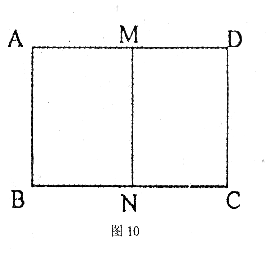
20.(本题满分8分)如图10,把矩形 对折,折痕为
对折,折痕为 ,矩形
,矩形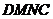 与矩形
与矩形 相似,已知
相似,已知 。
。
(1)求 的长。
的长。
(2)求矩形 与矩形
与矩形 的相似比。
的相似比。
21.(本题满分8分)把一副扑克牌中的3张黑桃牌(它们的正面牌数字分别为3、4、5)洗匀后正面朝下放在桌面上。
(1)如果从中随机抽取一张牌,那么牌面数字是4的概率是多少?
(2)小王和小李玩摸牌游戏,游戏规则如下:先由小王随机抽取一张牌,记下牌面数字后放回,洗匀后正面朝下,再由小李随机抽取一张牌,记下牌面数字。当2张牌的牌面数字相同时,小王赢;当2张牌的牌面数字不同时,小李赢。现请你利用树状图或列表法分析游戏规则对双方是否公平?并说明理由。
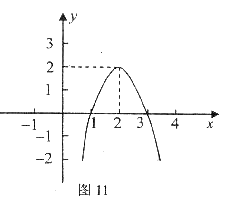
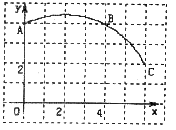
22.(本题满分12分)二次函数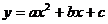 (a≠0)的图像如图11所示,根据图像解答下列问题:
(a≠0)的图像如图11所示,根据图像解答下列问题:
(1)写出方程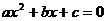 的两个根。
的两个根。
(2)写出不等式 >0的解集。
>0的解集。
(3)写出 随
随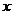 的增大而减小的自变量
的增大而减小的自变量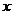 的取值范围。
的取值范围。
(4)若方程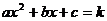 有两个不相等的实数根,求
有两个不相等的实数根,求 的取值范围。
的取值范围。
23.(本题满分9分)如图12,在正方形网格图中建立一直角坐标系,一条圆弧经过网格点A、B、C,请在网格中进行下列操作:
(1)请在图中确定该圆弧所在圆心D点的位置,D点坐标为 ;
(2)连接AD、CD,求⊙O的半径(结果保留根号)及扇形ADC的圆心角度数;
(3)若扇形DAC是某一个圆锥的侧面展开图,求该圆锥的底面半径(结果保留根号)。
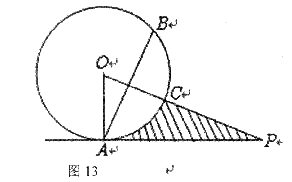
24.(本题满分9分)如图13,点P在圆O外,PA与圆O相切于A点,OP与圆周相交于C点,点B与点A关于直线PO对称,已知OA=4,PA= 。
。
求:
(1)∠POA的度数;
(2)弦AB的长;
(3)阴影部分的面积。
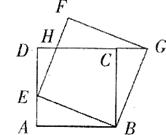
25.(本题满分12分)如图14,正方形ABCD的边长为1,点E是AD边上的动点,从点A沿AD向D运动,以BE为边,在BE的上方作正方形BEFG,连接CG。请探究:
(1)线段AE与CG是否相等?请说明理由。
(2)若设AE=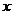 ,DH=
,DH= ,当
,当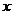 取何值时,
取何值时, 最大?
最大?
(3)连接BH,当点E运动到AD的何位置时,△BEH ∽△BAE?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com