
2008年甘肃省白银等九市州中考
数学试卷
抛物线 的顶点坐标是
的顶点坐标是 .
.
一、选择题:本大题共10小题,每小题3分,共30分.每小题给出的四个选项中,只有一项是符合题目要求的,将此选项的代号填入题后的括号内.
1.化简: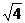 =( )
=( )
A.2
B.
2. 如下图,一个碗摆放在桌面上,则它的俯视图是( )

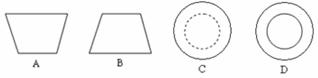
3. 2008年在北京举办的第29届奥运会的火炬传递在各方面都是创记录的:火炬境外传递城市19个,境内传递城市和地区116个,传递距离为137万公里,火炬手的总数达到21780人.用科学记数法表示21780为( )
A.2.178×105 B.2.178×
4. 如下图,小红和小丽在操场上做游戏,她们先在地上画出一个圆圈,然后蒙上眼在一定距离外向圆圈内投小石子,则投一次就正好投到圆圈内是( )
A.必然事件(必然发生的事件)
B.不可能事件(不可能发生的事件)
C.确定事件(必然发生或不可能发生的事件)
D.不确定事件(随机事件)
5.把不等式组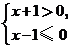 的解集表示在数轴上,正确的为( )
的解集表示在数轴上,正确的为( )

6.张颖同学把自己一周的支出情况,用如下图所示的统计图来表示.则从图中可以看出( )
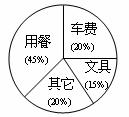
A.一周支出的总金额
B.一周各项支出的金额
C.一周内各项支出金额占总支出的百分比
D.各项支出金额在一周中的变化情况
7. 如下图四种正多边形的瓷砖图案.其中,是轴对称图形但不是中心对称的图形为( )

A.①③ B. ①④ C.②③ D.②④
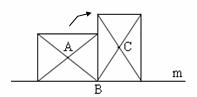
8.中央电视台2套“开心辞典”栏目中,有一期的题目如下图所示,两个天平都平衡,则与2个球体相等质量的正方体的个数为( )
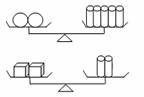
A.5
B.
9. 高速公路的隧道和桥梁最多.如下图是一个隧道的横截面,若它的形状是以O为圆心的圆的一部分,路面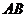 =
=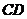 =
=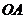 =( )
=( )
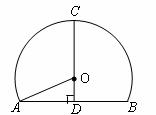
A.5
B.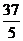 D.
D.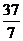
10.如下图,把矩形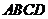 沿
沿 对折后使两部分重合,若
对折后使两部分重合,若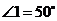 ,则
,则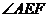 =( )
=( )
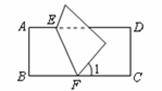
A.110° B.115° C.120° D.130°
二、填空题:本大题共8小题,每小题4分,共32分.把答案填在题中的横线上.
11. 若向南走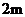 记作
记作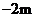 ,则向北走
,则向北走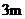 记作
记作 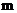 .
.
12.点P(-2,3)关于x轴的对称点的坐标是________.
13. 已知等腰三角形的一条腰长是5,底边长是6,则它底边上的高为 .
14. 抛物线 y=x2+x-4与y轴的交点坐标为 .
15. 如下图,将左边的矩形绕点B旋转一定角度后,位置如右边的矩形,则∠ABC=___ ___ .
16.某商店销售一批服装,每件售价150元,打8折出售后,仍可获利20元,设这种服装的成本价为每件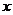 元,则x满足的方程是
.
元,则x满足的方程是
.
17. 一个函数具有下列性质:
①它的图像经过点(-1,1);②它的图像在二、四象限内; ③在每个象限内,函数值y随自变量x的增大而增大.则这个函数的解析式可以为 .
18. 如下图 (1)是一个等腰梯形,由6个这样的等腰梯形恰好可以拼出如下图 (2)所示的一个菱形.对于图(1)中的等腰梯形,请写出它的内角的度数或腰与底边长度之间关系的一个正确结论: .
三、解答题(一):本大题共5小题,共38分.解答时,应写出必要的文字说明、证明过程或演算步骤.
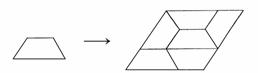
19. (6分) 化简: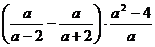
20.(6分)请你类比一条直线和一个圆的三种位置关系,在下图①、②、③中,分别各画出一条直线,使它与两个圆都相离、都相切、都相交,并在图④中也画上一条直线,使它与两个圆具有不同于前面3种情况的位置关系.

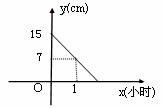
21.(8分)下图是某种蜡烛在燃烧过程中高度与时间之间关系的图像,由图像解答下列问题:
(1)此蜡烛燃烧1小时后,高度为 cm;经过 小时燃烧完毕;
(2)求这个蜡烛在燃烧过程中高度与时间之间关系的解析式.
22.(8分)如下图,在 ABCD中,点E是CD的中点,AE的延长线与BC的延长线相交于点F.
ABCD中,点E是CD的中点,AE的延长线与BC的延长线相交于点F.
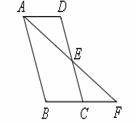
(1)求证:△ADE≌△FCE;
(2)连结AC、DF,则四边形ACFD是下列选项中的( ).
A.梯形 B.菱形 C.正方形 D.平行四边形
23.(10分) 某校八年级320名学生在电脑培训前后各参加了一次水平相同的考试,考试成绩都以同一标准划分成“不及格”、“及格”和“优秀”三个等级.为了了解电脑培训的效果,用抽签方式得到其中32名学生培训前后两次考试成绩的等级,并绘制成如下图的统计图,试结合图形信息回答下列问题:
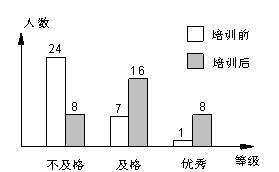
(1) 这32名学生培训前后考试成绩的中位数所在的等级分别是 、 ;
(2)估计该校整个八年级学生中,培训后考试成绩的等级为“及格”与“优秀”的学生共有多少名?
四、解答题(二):本大题共5小题,共50分.解答时,应写出必要的文字说明、证明过程或演算步骤.
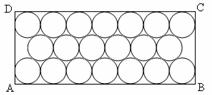
24.(8分))下图是一盒刚打开的“兰州”牌香烟,图 (1)是它的横截面(矩形ABCD),已知每支香烟底面圆的直径是

 (1)
(1)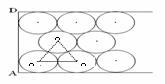 (2)
(2)
(1) 矩形ABCD的长AB= mm;
(2)利用图(2)求矩形ABCD的宽AD.(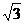 ≈1.73,结果精确到
≈1.73,结果精确到
25.(10分)如下图①,在一幅矩形地毯的四周镶有宽度相同的花边. 如下图②,地毯中央的矩形图案长

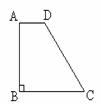
26.(10分)如下图,在梯形ABCD中,AD∥BC,∠B=90°,AD=2,BC=5,tanC=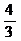 .
.
(1)求点D到BC边的距离;
(2)求点B到CD边的距离.
27.(10分)小明和小慧玩纸牌游戏. 图是同一副扑克中的4张扑克牌的正面,将它们正面朝下洗匀后放在桌上,小明先从中抽出一张,小慧从剩余的3张牌中也抽出一张.

小慧说:若抽出的两张牌的数字都是偶数,你获胜;否则,我获胜.
(1)请用树状图表示出两人抽牌可能出现的所有结果;
(2)若按小慧说规则进行游戏,这个游戏公平吗?请说明理由.
28.(12分)如下图,在平面直角坐标系中,四边形OABC是矩形,点B的坐标为(4,3).平行于对角线AC的直线m从原点O出发,沿x轴正方向以每秒1个单位长度的速度运动,设直线m与矩形OABC的两边分别交于点M、N,直线m运动的时间为t(秒).
(1) 点A的坐标是__________,点C的坐标是__________;
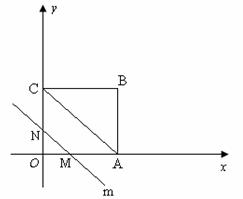
(2) 当t= 秒或 秒时,MN=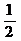 AC;
AC;
(3) 设△OMN的面积为S,求S与t的函数关系式;
(4) 探求(3)中得到的函数S有没有最大值?若有,求出最大值;若没有,要说明理由.
附加题 (12分)
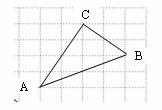
1.(5分)如下图,网格小正方形的边长都为1.在ㄓABC中,试画出三边的中线(顶点与对边中点连结的线段),然后探究三条中线位置及其有关线段之间的关系,你发现了什么有趣的结论?请说明理由.
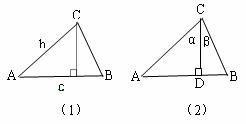
2.(7分)如下图(1),由直角三角形边角关系,可将三角形面积公式变形,
得 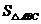 =
=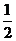 bc?sin∠A. ①
bc?sin∠A. ①
即三角形的面积等于两边之长与夹角正弦之积的一半.
如下图(2),在ㄓABC中,CD⊥AB于D,∠ACD=α, ∠DCB=β.
∵ 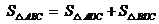 , 由公式①,得
, 由公式①,得
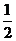 AC?BC?sin(α+β)=
AC?BC?sin(α+β)= 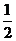 AC?CD?sinα+
AC?CD?sinα+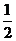 BC?CD?sinβ,
BC?CD?sinβ,
即 AC?BC?sin(α+β)= AC?CD?sinα+BC?CD?sinβ. ②
你能利用直角三角形边角关系,消去②中的AC、BC、CD吗?不能,说明理由;能,写出解决过程.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com