
2008年齐齐哈尔市初中毕业学业考试
数学试卷
考生注意:
1.考试时间120分钟
2.全卷共三道大题,总分120分
一、填空题(每空3分,满分33分)
1.在抗震救灾过程中,共产党员充分发挥了先锋模范作用,截止
2.函数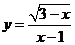 中,自变量
中,自变量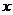 的取值范围是
.
的取值范围是
.
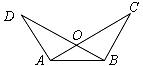
3.如图,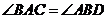 ,请你添加一个条件:
,使
,请你添加一个条件:
,使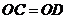 (只添一个即可).
(只添一个即可).
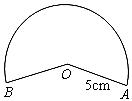
4.如图,小明想用图中所示的扇形纸片围成一个圆锥,已知扇形的半径为 cm,那么围成的圆锥的高度是
cm.
cm,那么围成的圆锥的高度是
cm.
5.如图,某商场正在热销2008年北京奥运会的纪念品,小华买了一盒福娃和一枚奥运徽章,已知一盒福娃的价格比一枚奥运徽章的价格贵120元,则一盒福娃价格是 元.

6.有一个正十二面体,12个面上分别写有1~12这12个整数,投掷这个正十二面体一次,向上一面的数字是3的倍数或4的倍数的概率是 .

7.如图,矩形 中,
中,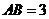 cm,
cm,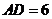 cm,点
cm,点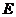 为
为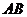 边上的任意一点,四边形
边上的任意一点,四边形
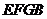 也是矩形,且
也是矩形,且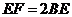 ,则
,则
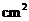 .
.
8.一幅图案.在某个顶点处由三个边长相等的正多边形镶嵌而成.其中的两个分别是正方形和正六边形,则第三个正多边形的边数是 .
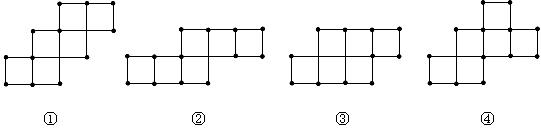
9.下列各图中, 不是正方体的展开图(填序号).
10.三角形的每条边的长都是方程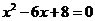 的根,则三角形的周长是
.
的根,则三角形的周长是
.
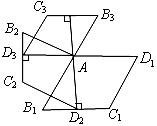
11.如图,菱形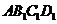 的边长为1,
的边长为1,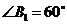 ;作
;作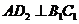 于点
于点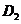 ,以
,以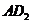 为一边,做第二个菱形
为一边,做第二个菱形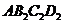 ,使
,使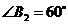 ;作
;作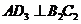 于点
于点 ,以
,以 为一边做第三个菱形
为一边做第三个菱形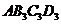 ,使
,使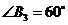 ;
;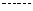 依此类推,这样做的第
依此类推,这样做的第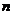 个菱形
个菱形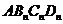 的边
的边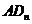 的长是
.
的长是
.
二、选择题(每题3分,满分27分)
12.下列各运算中,错误的个数是( )
①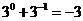 ②
②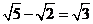 ③
③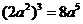 ④
④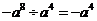
A.1 B.
13.用电器的输出功率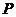 与通过的电流
与通过的电流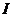 、用电器的电阻
、用电器的电阻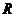 之间的关系是
之间的关系是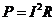 ,下面说法正确的是( )
,下面说法正确的是( )
A.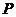 为定值,
为定值,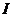 与
与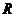 成反比例 B.
成反比例 B.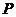 为定值,
为定值,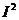 与
与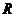 成反比例
成反比例
C.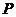 为定值,
为定值,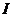 与
与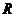 成正比例 D.
成正比例 D.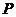 为定值,
为定值,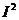 与
与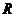 成正比例
成正比例
14.为紧急安置100名地震灾民,需要同时搭建可容纳6人和4人的两种帐篷,则搭建方案共有( )
A.8种 B.9种 C.16种 D.17种
15.对于抛物线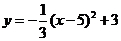 ,下列说法正确的是( )
,下列说法正确的是( )
A.开口向下,顶点坐标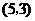 B.开口向上,顶点坐标
B.开口向上,顶点坐标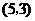
C.开口向下,顶点坐标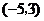 D.开口向上,顶点坐标
D.开口向上,顶点坐标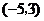
16.下列图案中是中心对称图形的是( )

17.关于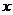 的分式方程
的分式方程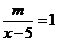 ,下列说法正确的是( )
,下列说法正确的是( )
A.方程的解是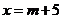 B.
B.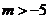 时,方程的解是正数
时,方程的解是正数
C.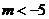 时,方程的解为负数 D.无法确定
时,方程的解为负数 D.无法确定
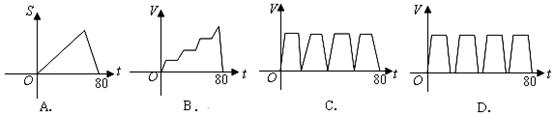
18.5月23日8时40分,哈尔滨铁路局一列满载着2400吨“爱心”大米的专列向四川灾区进发,途中除3次因更换车头等原因必须停车外,一路快速行驶,经过80小时到达成都.描述上述过程的大致图象是( )
19.已知5个正数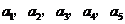 的平均数是
的平均数是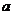 ,且
,且 ,则数据
,则数据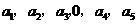 的平均数和中位数是( )
的平均数和中位数是( )
A.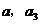 B.
B.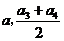 C.
C.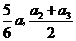 D.
D.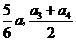
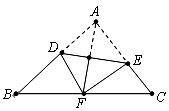
20.如图,将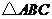 沿
沿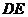 折叠,使点
折叠,使点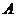 与
与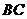 边的中点
边的中点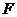 重合,下列结论中:①
重合,下列结论中:①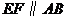 且
且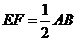 ;②
;②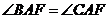 ;
;
③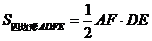 ;
;
④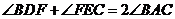 ,正确的个数是( )
,正确的个数是( )
A.1 B.2 C.3 D.4
三、解答题(满分60分)
21.(本小题满分5分)
先化简: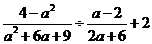 ,再任选一个你喜欢的数代入求值.
,再任选一个你喜欢的数代入求值.
22.(本小题满分6分)
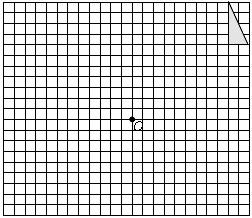
如图,方格纸中每个小正方形的边长都是单位1.
(1)平移已知直角三角形,使直角顶点与点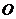 重合,画出平移后的三角形.
重合,画出平移后的三角形.
(2)将平移后的三角形绕点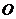 逆时针旋转
逆时针旋转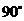 ,画出旋转后的图形.
,画出旋转后的图形.
(3)在方格纸中任作一条直线作为对称轴,画出(1)和(2)所画图形的轴对称图形,得到一个美丽的图案.
23.(本小题满分6分)
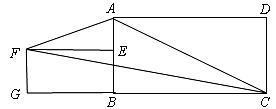
有一底角为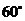 的直角梯形,上底长为10cm,与底垂直的腰长为10cm,以上底或与底垂直的腰为一边作三角形,使三角形的另一边长为15cm,第三个顶点落在下底上.请计算所作的三角形的面积.
的直角梯形,上底长为10cm,与底垂直的腰长为10cm,以上底或与底垂直的腰为一边作三角形,使三角形的另一边长为15cm,第三个顶点落在下底上.请计算所作的三角形的面积.
24.(本小题满分7分)
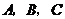 三名大学生竞选系学生会主席,他们的笔试成绩和口试成绩(单位:分)分别用了两种方式进行了统计,如表一和图一:
三名大学生竞选系学生会主席,他们的笔试成绩和口试成绩(单位:分)分别用了两种方式进行了统计,如表一和图一:
表一
A
B
C
笔试
85
95
90
口试
80
85

(1)请将表一和图一中的空缺部分补充完整.
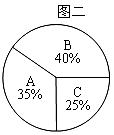
(2)竞选的最后一个程序是由本系的300名学生进行投票,三位候选人的得票情况如图二(没有弃权票,每名学生只能推荐一个),请计算每人的得票数.
(3)若每票计1分,系里将笔试、口试、得票三项测试得分按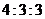 的比例确定个人成绩,请计算三位候选人的最后成绩,并根据成绩判断谁能当选.
的比例确定个人成绩,请计算三位候选人的最后成绩,并根据成绩判断谁能当选.
25.(本小题满分8分)
武警战士乘一冲锋舟从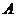 地逆流而上,前往
地逆流而上,前往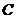 地营救受困群众,途经
地营救受困群众,途经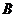 地时,由所携带的救生艇将
地时,由所携带的救生艇将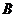 地受困群众运回
地受困群众运回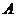 地,冲锋舟继续前进,到
地,冲锋舟继续前进,到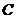 地接到群众后立刻返回
地接到群众后立刻返回 地,途中曾与救生艇相遇.冲锋舟和救生艇距
地,途中曾与救生艇相遇.冲锋舟和救生艇距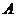 地的距离
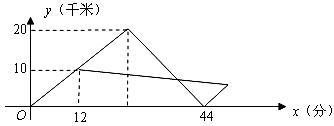
地的距离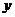 (千米)和冲锋舟出发后所用时间
(千米)和冲锋舟出发后所用时间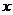 (分)之间的函数图象如图所示.假设营救群众的时间忽略不计,水流速度和冲锋舟在静水中的速度不变.
(分)之间的函数图象如图所示.假设营救群众的时间忽略不计,水流速度和冲锋舟在静水中的速度不变.
(1)请直接写出冲锋舟从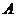 地到
地到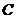 地所用的时间.
地所用的时间.
(2)求水流的速度.
(3)冲锋舟将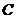 地群众安全送到
地群众安全送到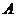 地后,又立即去接应救生艇.已知救生艇与
地后,又立即去接应救生艇.已知救生艇与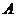 地的距离
地的距离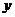 (千米)和冲锋舟出发后所用时间
(千米)和冲锋舟出发后所用时间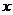 (分)之间的函数关系式为
(分)之间的函数关系式为 ,假设群众上下船的时间不计,求冲锋舟在距离
,假设群众上下船的时间不计,求冲锋舟在距离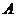 地多远处与救生艇第二次相遇?
地多远处与救生艇第二次相遇?
26.(本小题满分8分)
已知:正方形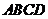 中,
中,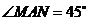 ,
,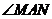 绕点
绕点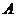 顺时针旋转,它的两边分别交
顺时针旋转,它的两边分别交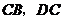 (或它们的延长线)于点
(或它们的延长线)于点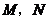 .
.
当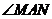 绕点
绕点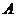 旋转到
旋转到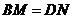 时(如图1),易证
时(如图1),易证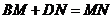 .
.
(1)当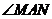 绕点
绕点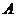 旋转到
旋转到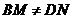 时(如图2),线段
时(如图2),线段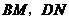 和
和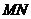 之间有怎样的数量关系?写出猜想,并加以证明.
之间有怎样的数量关系?写出猜想,并加以证明.
(2)当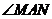 绕点
绕点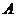 旋转到如图3的位置时,线段
旋转到如图3的位置时,线段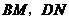 和
和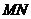 之间又有怎样的数量关系?请直接写出你的猜想.
之间又有怎样的数量关系?请直接写出你的猜想.

27.(本小题满分10分)
某工厂计划为震区生产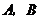 两种型号的学生桌椅500套,以解决1250名学生的学习问题,一套
两种型号的学生桌椅500套,以解决1250名学生的学习问题,一套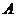 型桌椅(一桌两椅)需木料
型桌椅(一桌两椅)需木料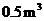 ,一套
,一套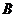 型桌椅(一桌三椅)需木料
型桌椅(一桌三椅)需木料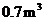 ,工厂现有库存木料
,工厂现有库存木料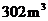 .
.
(1)有多少种生产方案?
(2)现要把生产的全部桌椅运往震区,已知每套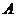 型桌椅的生产成本为100元,运费2元;每套
型桌椅的生产成本为100元,运费2元;每套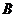 型桌椅的生产成本为120元,运费4元,求总费用
型桌椅的生产成本为120元,运费4元,求总费用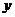 (元)与生产
(元)与生产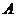 型桌椅
型桌椅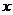 (套)之间的关系式,并确定总费用最少的方案和最少的总费用.(总费用
(套)之间的关系式,并确定总费用最少的方案和最少的总费用.(总费用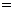 生产成本
生产成本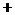 运费)
运费)
(3)按(2)的方案计算,有没有剩余木料?如果有,请直接写出用剩余木料再生产以上两种型号的桌椅,最多还可以为多少名学生提供桌椅;如果没有,请说明理由.
28.(本小题满分10分)
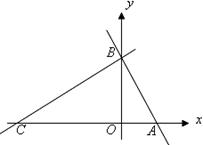
如图,在平面直角坐标系中,点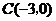 ,点
,点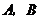 分别在
分别在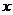 轴,
轴,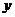 轴的正半轴上,且满足
轴的正半轴上,且满足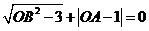 .
.
(1)求点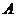 ,点
,点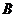 的坐标.
的坐标.
(2)若点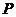 从
从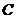 点出发,以每秒1个单位的速度沿射线
点出发,以每秒1个单位的速度沿射线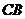 运动,连结
运动,连结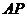 .设
.设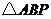 的面积为
的面积为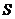 ,点
,点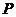 的运动时间为
的运动时间为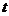 秒,求
秒,求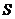 与
与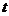 的函数关系式,并写出自变量的取值范围.
的函数关系式,并写出自变量的取值范围.
(3)在(2)的条件下,是否存在点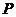 ,使以点
,使以点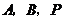 为顶点的三角形与
为顶点的三角形与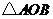 相似?若存在,请直接写出点
相似?若存在,请直接写出点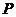 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com