
2007-2008学年度菏泽市定陶县第一学期九年级期末考试
数 学 试 题
一、精心选一选(每小题只有一个答案正确)(每小题3分,共36分)
1.下列各式中,正确的等式有
①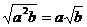 ②
②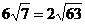 ③
③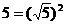 ④
④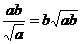
⑤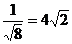 ⑥
⑥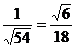
A.2个 B.3个 C.4个 D.5个
2.某产品原来每件600元,由于连续两次降价,现价为384元,如果两次降价的百分数相同。则每次降价的百分数为
A.90% B.80% C.60% D.20%
3.关于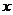 的一元二次方程(
的一元二次方程(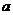 一1)
一1)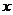 2+
2+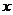 +
+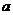 2-1=0的一个根是0,则
2-1=0的一个根是0,则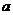 的值为
的值为
A.1
B.1或一l C.一l D.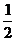
4.已知点A(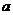 +b,3)和点B(一2,3
+b,3)和点B(一2,3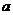 ―b)关于原点对称,则关于
―b)关于原点对称,则关于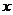 的方程
的方程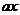 2+b
2+b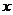 一2=0的根为
一2=0的根为
A.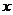 l=1,
l=1,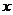 2=8 B.
2=8 B.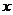 l=-1,
l=-1,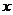 2=-8
2=-8
C.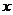 l=1,
l=1,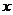 2=-8 D.
2=-8 D.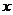 l=-1,
l=-1,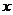 2=8
2=8
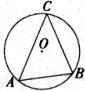
5.如图,∠C=45°,AB=4,则⊙O的半径为
A.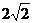 B.4 C.2
D.5
B.4 C.2
D.5
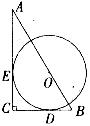
6.如图在Rt△ABC中,∠C=90°,BC=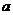 ,AC=b,以AB上一点O为圆心的⊙O,与BC切于点D,与AC切于点E,那么⊙O的半径等于( )
,AC=b,以AB上一点O为圆心的⊙O,与BC切于点D,与AC切于点E,那么⊙O的半径等于( )
A.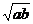 B.
B.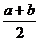 C.
C.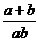 D.
D.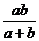
7.扇形的半径为30cm,圆心角为120°,用它做成一个圆锥的侧面,则圆锥的底面半径为
A.10cm B.20cm C.10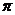 cm D.20
cm D.20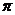 cm
cm
8.下图是用V型架托起两个钢管的横截面示意图,若V形角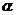 =60°,细钢管的外径为20cm,则粗钢管的外径为
=60°,细钢管的外径为20cm,则粗钢管的外径为
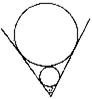
A.60ram B.50Int0 C.40ram D.30mm
9.某商场举办有奖销售活动,办法如下:凡购货满l00元者得奖券一张,多购多得,每10000张奖券为一个开奖单位,设特等奖1个,一等奖50个,二等奖100个,那么买100元商品的中奖概率应该是
A.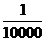 B.
B. C.
C. D.
D.
10.已知二次函数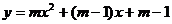 有最小值为0,则m的值为
有最小值为0,则m的值为
A.1或一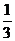 B.一
B.一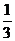 C.1 D.非上述答案
C.1 D.非上述答案
11.若将一个抛物线向右平移3个单位,再向上平移1个单位,所得的抛物线是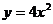 ,则这个抛物线的函数关系式是:
,则这个抛物线的函数关系式是:
A. B.
B.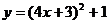
C.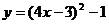 D.
D.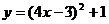
12.已知在△ABC中,∠B=90°,AB=6,BC=8,将△ABC沿DE折叠,使点C落在AB边上的C’处,并且C’D//BC,则CD的长是
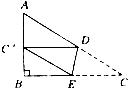
A.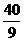 B.
B.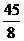 C.
C.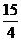 D.
D.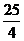
二、细心填一填(每小题3分,共36分)
13.设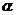 、
、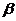 是方程
是方程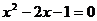 的两个根,则代数式
的两个根,则代数式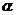 +
+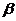 +
+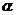
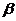 =_____________.
=_____________.
14.在平面直角坐标系中,A点的坐标为(3,4)将OA绕原点O逆时针旋转90°得到OA’,则点A’的坐标为___________.
15.某班同学测量学校升国旗的旗杆高度,在同一时刻量得某同学身高l.5米,影长为1米, 旗杆的影长为6米,则旗杆的高度为___________.
16.在Rt△ABC中,已知两直角边长为6和8,则其外接圆的面积为___________.
17.两圆半径长分别为R和r(R>r),圆心距为d,若关于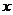 的方程
的方程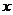 2―2r
2―2r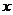 +(R―d)2=0有两相等的实数根,则两圆的位置关系为___________.
+(R―d)2=0有两相等的实数根,则两圆的位置关系为___________.
18.中央电视台大风车栏目图标如图①,其中心为O,半圆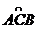 固定,其半径为2r,车轮为中心对称图形,轮片也是半圆形,小红通过观察发现车轮旋转过程中留在半圆
固定,其半径为2r,车轮为中心对称图形,轮片也是半圆形,小红通过观察发现车轮旋转过程中留在半圆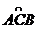 内的轮片面积是不变的,(如图②),这个不变的面积值是__________.
内的轮片面积是不变的,(如图②),这个不变的面积值是__________.

19.如图是一张电脑光盘的表面,两个圆心都是点O,大圆的弦AB所在直线是小圆的切线,切点为C.已知大圆的半径为5cm,小圆的半径为1cm,则弦A曰的长度为________.
20.一个口袋里装有红、绿、蓝三种颜色的小球(除颜色外,无差别),其中有6个红球,5个绿球,若任意摸出一个球为绿球的概率是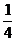 ,则任意摸出一个球为蓝球的概率是________.
,则任意摸出一个球为蓝球的概率是________.
21.抛物线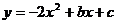 的顶点是(1,5),则b=________,c=________.
的顶点是(1,5),则b=________,c=________.
22.五边形ABCDE与五边形A’B’C’D’E’位似,对应边CD=2,C’D’=3,若位似中心P到A的距离为6,则P到A’的距离PA’ ________.
23.已知二次函数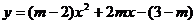 的图象开口向上,顶点在第三象限,且交于y轴的负半轴,则m的取值范围是________.
的图象开口向上,顶点在第三象限,且交于y轴的负半轴,则m的取值范围是________.
24.在△ABC中,AB= .
.
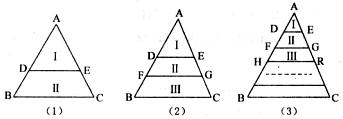
(1)如图(1)所示,DE∥BC,DE把△ABC分成面积相等的两部分,即SI=SⅡ,则AD=________.
(2)如图(2)所示,DE//FG//BC,DE、FG把△ABC分成面积相等的三部分,即SI=SⅡ=
SⅢ,则AD=________.
(3)如图(3)所示,DE//FG//HR……∥BC,DE,FG,HR……把△ABC分成面积相等的n部分,SI=SⅡ=SⅢ……,则AD=________.
三、耐心做一做(共48分)
25.(9分)化简,求值
(1)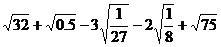
(2)已知(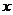 +9)2=169,(
+9)2=169,(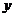 一l)3=-0.125
一l)3=-0.125
求: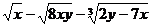
(3)若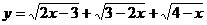 ,求
,求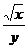 的值.
的值.
26.(8分)某百货大楼服装柜台在销售中发现“宝乐”牌童装平均每天可售出20件,每件盈利40元,为了迎接十一国庆节,商场决定采取适当的降价措施,扩大销售量,增加盈利,减少库存,经市场调查发现;如果每件童装降价4元,那么平均每天就可多售出8件,要想平均每天销售这种童装盈利1200元,那么每件童装应降价多少元?
27.(8分)如图(1)AB是⊙O的直径,AC是弦,直线EF和⊙O相切于点C,AD⊥EF,垂足为D,
(1)求证:∠DAC=∠BAC
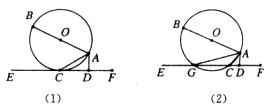
(2)若把直线EF向上平行移动,如图2,EF交⊙O于G、C两点,若题中的其它条件不变,这时与∠DAC相等的角是哪一个?为什么?
28.(8分)小明和小乐做摸球游戏,一只不透明的15袋里只放有3个红球和5个绿球,每个球除颜色外都相同,每次摸球前都将袋中的球充分搅匀,从中任意摸出一个球,记录颜色后再放回,若是红球小明得3分,若是绿球小乐得2分,游戏结束时得分多者获胜.
(1)你认为这个游戏对双方公平吗?
(2)若你认为公平,请说明理由;若你认为不公平,也请说明理由,并修改规则,使该游戏对双方都公平.
29.(6分)如图,点 ABCD的边BC的延长线上,AE交CD于点F,且CF=
ABCD的边BC的延长线上,AE交CD于点F,且CF=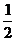 FD
FD
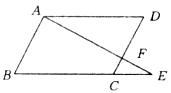
求:S△ECF :S△EBA
30.(9分)在平面直角坐标系中,△AOB的位置,如图所示,已知∠AOB=90°,AO=BO,点A的坐标为(一3,1)
(1)求点B的坐标;
(2)求过A、O、B三点的抛物线的解析式;
(3)设点B关于抛物线的对称轴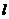 的对称点为B.
的对称点为B.
求△AB1B的面积.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com