
2007-2008学年度烟台市莱州第二学期初一期末质量检测
数学试卷
一、耐心填一填(每题3分,共30分)
1.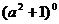 =
.
=
.
2.已知 ,则
,则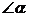 的补角等于 .
的补角等于 .
3.请写一个含有字母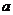 和
和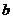 ,次数是3的单项式 .
,次数是3的单项式 .
4.氢原子的质量为0.000 000 000 000
000 000 000 001 673
5.在以后的比赛中,中国足球队获世界杯冠军是 (填“可能事件”或“不可能事件”).
6.计算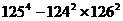 的结果是
.
的结果是
.
7.已知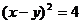 ,
,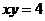 ,则
,则 =
.
=
.
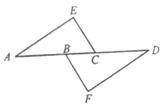
8.如图,∠A=∠D,AB=CD,要使△AEC≌△DFB,还需要补充一个条件,这个条件可以是 (只需填写一个).
9.一个盒子中有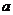 个红球和
个红球和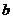 黄球,每个球除了颜色外都相同.若从盒子中摸到红球的可能性小于摸到黄球的可能性,则
黄球,每个球除了颜色外都相同.若从盒子中摸到红球的可能性小于摸到黄球的可能性,则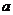 与
与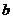 的大小关系是 .
的大小关系是 .
10.一个多项式减去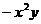 后等于
后等于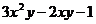 ,则这个多项式是
.
,则这个多项式是
.
二、细心选一选(每小题3分,共30分)
1.下列各式能用平方差公式进行计算的是 ( )
A.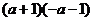 B.
B.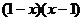
C.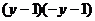 D.
D.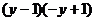
2.下列各式计算正确的是 ( )
A.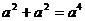 B.
B.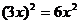
C.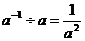 D.
D.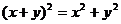
3.下列说法:①0是单项式;②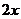 是多项式
是多项式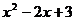 中的一项;③
中的一项;③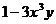 是三次二项式;④
是三次二项式;④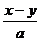 是整式.其中正确的有 ( )
是整式.其中正确的有 ( )
A.1个 B.2个 C.3个 D.4个
4.有下列说法:①两条直线被第三条直线所截,内错角相等;②相等的角是对顶角;③同角或等角的余角相等;④三角形的三条高交于一点.其中正确的有 ( )
A.1个 B.2个 C.3个 D.4个
5.如图,Rt△ABC中,∠ACB=90°,DE过点C且平行于AB,若∠BCE=35°,则∠A的度数为 ( )
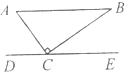
A.35° B.45° C.55° D.65°
6.通讯卫星的高度是3.6×
A.1.2× 米/秒 B.2.4×10
米/秒 B.2.4×10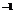 米/秒
米/秒
C.2.4×10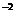 米/秒 D.3.6×10
米/秒 D.3.6×10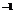 米/秒
米/秒
7.若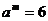 ,
,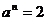 ,则
,则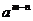 的值等于 ( )
的值等于 ( )
A.3 B.4 C.8 D.12
8.一个三角形的两边分别是5和11,若第三边是整数,则这个三角形的最小周长是( )
A.21 B.22 C.23 D.24
9.若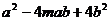 是完全平方式,则
是完全平方式,则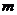 的值为( )
的值为( )
A.1 B.-1 C.1或-1 D.2或-2
10.如图,在Rt△ABC中,CD是斜边上的高.DE⊥BC于E,DF⊥AC于F.则图中与
∠B相等的角有 ( )
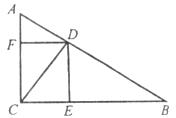
A.1个 B.2个 C.3个 D.4个
三、完成下列各题(第1题4分,第2题5分,满分9分)
1.计算:
2.已知: ,
,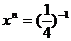 求
求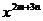 的值.
的值.
四、尺规作图(满分6分)
已知∠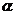 和线段
和线段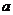 ,用尺规作△ABC,使AB=
,用尺规作△ABC,使AB=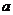 ,∠CAB=∠CBA=2∠
,∠CAB=∠CBA=2∠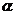 .
.
要求:写出作法,保留作图痕迹.

五、(满分7分)
已知A=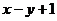 ,B=
,B=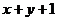 ,C=
,C=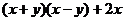 ,两同学对
,两同学对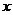 、
、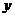 分别取了不同的值,求出的A、B、C的值不同,但A×B-C的值却总是一样的.因此两同学得出结论:无论
分别取了不同的值,求出的A、B、C的值不同,但A×B-C的值却总是一样的.因此两同学得出结论:无论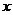 、
、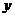 取何值,A×B-C的值都不发生变化.你认为这个结论正确吗?请你说明理由。
取何值,A×B-C的值都不发生变化.你认为这个结论正确吗?请你说明理由。
六、(满分7分)
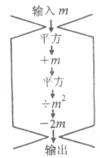
小明设计了一个运算程序(如图),分别输入不同的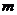 (
(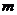 ≠0)值,可以输出不同结果.请解决下列问题:
≠0)值,可以输出不同结果.请解决下列问题:
1.无论输入何值,输出的结果是负数属于什么事件?为什么?
2.输出的结果一定大于1,还是很可能大于1?为什么?
七、(满分8分)
如图所示,用长为20的铁丝焊接成一个长方形,设长方形的一边为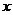 ,面积为
,面积为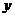 ,随着
,随着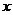 的变化,
的变化,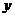 的值也随之变化.
的值也随之变化.
1.写出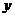 与
与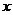 之间的关系式,并指出在这个变化中,哪个是自变量?哪个是因变量?
之间的关系式,并指出在这个变化中,哪个是自变量?哪个是因变量?
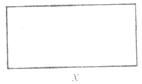
2.用表格表示当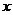 从1变化到9时(每次增加l),
从1变化到9时(每次增加l),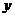 的相应值;
的相应值;
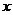
1
y
3.当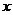 为何值时,
为何值时, 的值最大?
的值最大?
八、(满分9分)
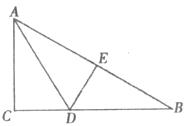
如图,在Rt△ABC中,∠C=90°,∠B=30°.AD是角平分线,AE=AC.
1.求∠BDE的度数;
2.DE⊥AB吗?AE=BE吗?为什么?
九、(满分14分)
“龟兔赛跑”的故事同学们都非常熟悉,图中的线段OD和折线OABC表示“龟兔赛跑”时路程与时间的关系,请你根据图中给出的信息,解决下列问题.
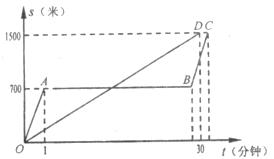
1.填空:折线OABC表示赛跑过程中 的路程与时间的关系,线段OD表示赛跑过程中 的路程与时间的关系.赛跑的全程是 米。
2.兔子在起初每分钟跑多少米?乌龟每分钟爬多少米?
3.乌龟用了多少分钟追上了正在睡觉的兔子?
4.兔子醒来,以48千米/时的速度跑向终点,结果还是比乌龟晚到了0.5分钟,请你算算兔子中间停下睡觉用了多少分钟?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com