
2008-2009学年度日照市五莲第一学期八年级学科学业水平监测
数学试卷
(时间l00分钟 满分l20分)
一、选择题:(本题共l2小题,第l-8小题,每小题3分,第9-12小题,每小题4分,共40分。在每小题给出的四个选项中,只有一项是正确的)
1.在实数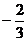 ,0,
,0,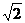 ,
, ,
,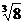 中,无理数有
中,无理数有
A.1个 B.2个 C.3个 D.4个
2.l6的平方根是
A.4 B.士
3.下列运算正确的是
A. B.
B.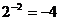
C. D.
D.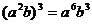
4.任意给定一个非零数,按下列程序计算,最后输出的结果是

A.m B.m
5.下列各条件中,不能唯一作直角三角形的是
A.已知两条直角边 B.已知一锐角及斜边
C.已知一锐角及其邻边 D.已知一锐角及其对边
6.一个正方体的水晶砖,体积为l
A.
C.
7.如果x2+mx+16是一个完全平方式,那么m的值为
A.8 B.-
8.已知等腰三角形的一个内角为50°,则这个等腰三角形的顶角为
A.50° B.80° C.50°或80° D.40°或65°
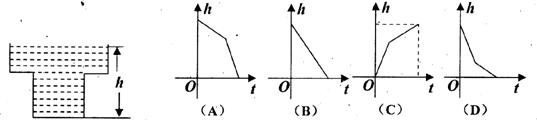
9.某蓄水池的横断面示意图如下图,分深水区和浅水区,如果这个注满水的蓄水池以固定的流量把水全部放出.下面的图像能大致表示水的深度h和放水时间t之间的关系的是
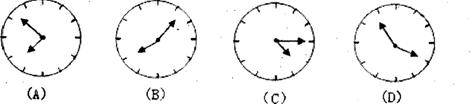
10.小华在镜中看到身后墙上的钟,你认为实际时间最接近8点的是
11.如图,每个小正方形的边长为l,把阴影部分剪下来,用剪下来的阴影部分拼成一个正方形,那么新正方形的边长是

A.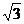 B.
B.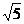 D.
D.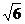
12.甲、乙两同学骑自行车从A地沿同一条路到B地,已知乙比甲先出发,他们离出发地的距离s(km)和骑行时间t(h)之间的函数关系如图所示,给出下列说法:
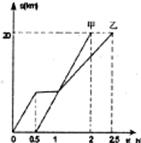
(1)他们都骑行了
(2)乙在途中停留了0.5h;
(3)甲、乙两人同时到达目的地;
(4)相遇后,甲的速度小于乙的速度.
根据图像信息,以上说法正确的有
A.1个 B.2个 C.3个 D.4个
二、填空题:(本题共6小题,每小题3分,共18分。请把最终结果直接填在横线上)
13.因式分解: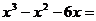 ___________.
___________.
14.如果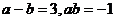 ,则
,则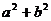 的值等于__________.
的值等于__________.
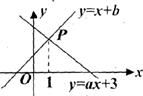
15.如图,已知函数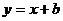 和
和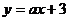 的图像交点为
的图像交点为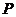 ,则不等式
,则不等式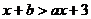 的解集__________.
的解集__________.
16.若直线y=kx+3与坐标轴所围成的三角形的面积为l2,则k的值为__________.
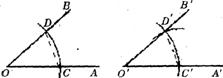
17.用直尺和圆规作一个角等于已知角的示意图如下图所示,则说明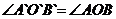 的依据是__________________.
的依据是__________________.
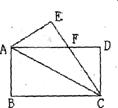
18.如图将长方形ABCD沿AC折叠,使点B落在点E处,若长方形ABCD的周长为
三、解答题:(本题共6小题,共62分.解答题都应写出文字说明、证明过程或推演步骤)
19.(每小题6分,共l2分)
(1)已知: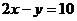 ,求
,求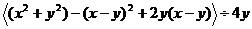 的值.
的值.
(2)分解因式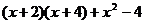 .
.
20.(本题满分6分)
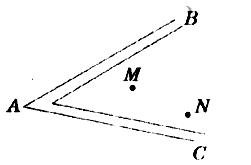
如图,某中学两个班的学生分别在M、N两处参加植树劳动,现要在道路AB、AC的交叉区域内设置一个茶水供应点P,使点P到点M,N的距离相等,且到两条道路的距离也相等,现在请你画出点P的位置的示意图(不写作法,只保留作图痕迹)。
21.(本题满分l0分)
两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,B,C,E在同一条直线上,连结DC.
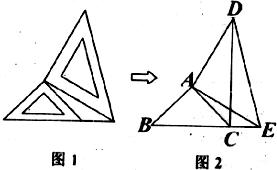
(1)请找出 图2中的全等三角形,并给予证明(说明:结论中不得含有未标识的字母);
(2)证明:DC⊥BE
22.(本题满分12分)
已知:点O到△ABC的两边AB、AC所在真线的距离相等,且OB=OC。
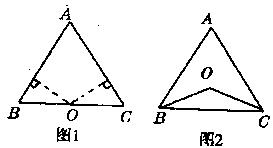
(1)如图l,若点O在BC上,求证:AB=AC;
(2)如图2,若点O在△ABC的内部,求证:AB=AC;
(3)若点O在△ABC的外部,AB=AC成立吗?请画图表示.
23.(本题满分l2分)
某市组织l0辆汽车装运完A、B、C三种不同品质的橘子共l00吨到外地销售,按计划l0辆汽车都要装满,且每辆汽车只能装同一种橘子,根据下表提供的信息,解答以下问题:
橘子品种
A
B
C
每辆汽车云载量(吨)
12
10
8
每吨橘子获利(千元)
3
4
2
(1)设装运A种橘子的车辆数为x,装运B种橘子的车辆数为y,求与x之间的函数关系式;
(2)如果装运每种橘子的车辆数都不少于2辆,那么车辆的安排方案有几种?并写出每种安排方案;
(3)若要使此次销售获利最大,应采用哪种安排方案?并求出最大利润的值.
24.(本题满分l0分)
实验与探究:
如图,在平面直角坐标系中,直线 是第一、三象限的角平分线.
是第一、三象限的角平分线.
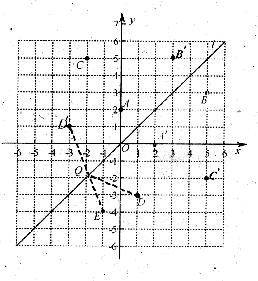
(1)由图观察易知A(0,2)关于直线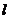 的对称点A′的坐标为(2,0),请在图中分别标明B(5,3)、C(-2,5)关于直线的对称点B′、C′的位置,并写出他们的坐标:
的对称点A′的坐标为(2,0),请在图中分别标明B(5,3)、C(-2,5)关于直线的对称点B′、C′的位置,并写出他们的坐标:
B′_______________、C′_________________;
归纳与发现:
运用与拓广:
(2)结合图形观察以上三组点的坐标,你会发现:坐标平面内任一点P(a,6)关于第一、三象限的角平分线的对称点P′的坐标为____________(不必证明);
(3)已知两点D(1,-3)、E(-1,-4),试在直线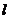 上确定一点Q,使点Q到D、E两点的距离之和最小,并求出Q点坐标.
上确定一点Q,使点Q到D、E两点的距离之和最小,并求出Q点坐标.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com