
2009年浙江省台州市初中学业水平考试
数学试卷
亲爱的考生:
欢迎参加考试!请你认真审题,积极思考,仔细答题,发挥最佳水平。答题时,请注意以下几点:
1.全卷共4页,满分150分,考试时间120分钟。
2.答案必须写在答题纸相应的位置上,写在试题卷、草稿纸上无效。
3.答题前,请认真阅读答题纸上的《注意事项》,按规定答题。
4.本次考试不得使用计算器,请耐心解答。祝你成功!
一、选择题(本题有10小题,每小题4分,共40分.请选出各题中一个符合题意的正确选项,不选、多选、错选,均不给分)
1.如图,由三个相同小正方体组成的立体图形的主视图是( )
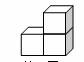

2.数据1,2,2,3,5的众数是( )
A.1
B.
3.单词NAME的四个字母中,是中心对称图形的是( )
A.N B.A C.M D.E
4.大圆半径为6,小圆半径为3,两圆圆心距为10,则这两圆的位置关系为( )
A.外离 B.外切 C.相交 D.内含
5.下列运算正确的是 ( )

A.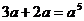 B.
B.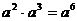
C.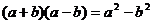 D.
D.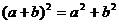
6.用配方法解一元二次方程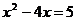 的过程中,配方正确的是( )
的过程中,配方正确的是( )
A.(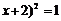 B.
B.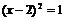 C.
C.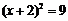 D.
D.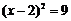
7.盒子里有3支红色笔芯,2支黑色笔芯,每支笔芯除颜色外均相同.从中任意拿出一支笔芯,则拿出黑色笔芯的概率是( )
A.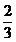 B.
B.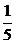 C.
C.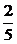 D.
D. 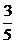
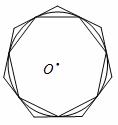
8.如图,⊙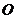 的内接多边形周长为3 ,⊙
的内接多边形周长为3 ,⊙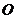 的外切多边形周长为3.4,则下列各数中与此圆的周长最接近的是( )
的外切多边形周长为3.4,则下列各数中与此圆的周长最接近的是( )
A. B.
B.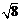 C.
C. D.
D.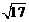
9.已知二次函数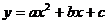 的
的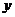 与
与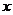 的部分对应值如下表:
的部分对应值如下表:
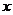
…
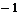
0
1
3
…
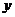
…
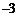
1
3
1
…
则下列判断中正确的是( )
A.抛物线开口向上 B.抛物线与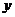 轴交于负半轴
轴交于负半轴
C.当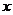 =4时,
=4时,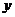 >0
D.方程
>0
D.方程 的正根在3与4之间
的正根在3与4之间
10.若将代数式中的任意两个字母交换,代数式不变,则称这个代数式为完全对称式,如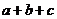 就是完全对称式.下列三个代数式:①
就是完全对称式.下列三个代数式:①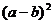 ;②
;②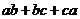 ;
;
③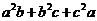 .其中是完全对称式的是( )
.其中是完全对称式的是( )
A.①② B.①③ C. ②③ D.①②③
二、填空题(本题有6小题,每小题5分,共30分)
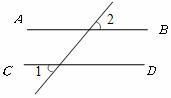
11.如图,已知直线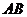 ∥
∥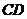 ,∠1=50°,则∠2=
.
,∠1=50°,则∠2=
.
12.请你写出一个图象在第一、三象限的反比例函数.答: .
13.随机从甲、乙两块试验田中各抽取100株麦苗测量高度,计算平均数和方差的结果为:
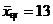 ,
,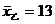 ,
,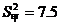 ,
,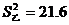 ,则小麦长势比较整齐的试验田是
,则小麦长势比较整齐的试验田是
(填“甲”或“乙”).
14.在课外活动跳绳时,相同时间内小林跳了90下,小群跳了120下.已知小群每分钟比小林多跳20下,设小林每分钟跳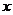 下,则可列关于
下,则可列关于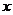 的方程为 .
的方程为 .
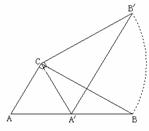
15.如图,三角板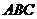 中,
中,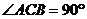 ,
,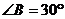 ,
,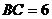 .三角板绕直角顶点
.三角板绕直角顶点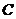 逆时针旋转,当点
逆时针旋转,当点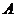 的对应点
的对应点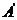 落在
落在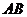 边的起始位置上时即停止转动,则点
边的起始位置上时即停止转动,则点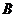 转过的路径长为 .
转过的路径长为 .
16.将正整数1,2,3,…从小到大按下面规律排列.若第4行第2列的数为32,则
①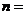 ;②第
;②第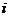 行第
行第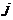 列的数为
(用
列的数为
(用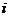 ,
,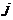 表示).
表示).
第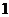 列
列
第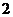 列
列
第 列
列
…
第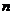 列
列
第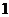 行
行
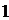
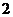

…
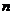
第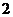 行
行
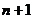
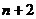
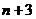
…
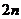
第 行
行
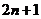
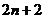
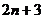
…
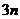
…
…
…
…
…
…
三、解答题(本题有8小题,第17~20题每题8分,第21题10分,第22,23题每题12分,第24题14分,共80分)
17.计算: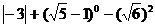 .
.
18.解不等式组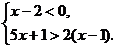
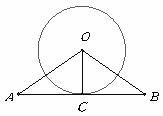
19.如图,等腰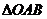 中,
中,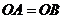 ,以点
,以点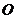 为圆心作圆与底边
为圆心作圆与底边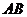 相切于点
相切于点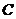 .
.
求证: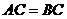 .
.
20.如图,有一段斜坡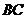 长为
长为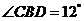 ,为方便残疾人的轮椅车通行,
,为方便残疾人的轮椅车通行,
现准备把坡角降为5°.
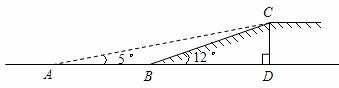
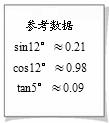
(1)求坡高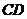 ;
;
(2)求斜坡新起点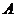 与原起点
与原起点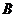 的距离(精确到
的距离(精确到
21.如图,直线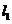 :
: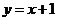 与直线
与直线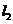 :
: 相交于点
相交于点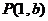 .
.
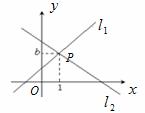
(1)求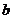 的值;
的值;
(2)不解关于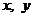 的方程组
的方程组 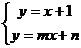 请你直接写出它的解;
请你直接写出它的解;
(3)直线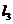 :
: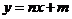 是否也经过点
是否也经过点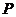 ?请说明理由.
?请说明理由.
22.台州素有“七山一水两分田”之说,据此画成统计图1.图2是台州市2004~2008年的人口统计图(单位:万人).

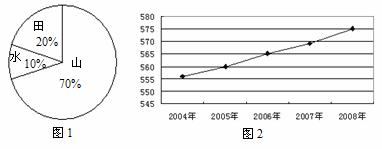
(1)请你计算扇形统计图中表示“田”的扇形圆心角的度数;
(2)请你指出台州市2004~2008年的人口变化趋势,并据此推断台州市2004~2008年人均耕地面积是不断增加还是不断减少?(人均耕地面积=耕地总面积÷人口)
(3)结合统计图和资料的信息,计算台州市2008年耕地总面积约是多少亩(结果用科学记数法表示).
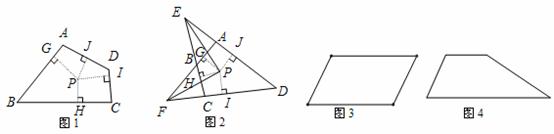
23.定义:到凸四边形一组对边距离相等,到另一组对边距离也相等的点叫凸四边形的准内点.如图1,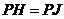 ,
,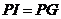 ,则点
,则点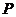 就是四边形
就是四边形 的准内点.
的准内点.
(1)如图2, 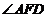 与
与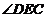 的角平分线
的角平分线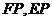 相交于点
相交于点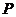 .
.
求证:点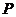 是四边形
是四边形 的准内点.
的准内点.
(2)分别画出图3平行四边形和图4梯形的准内点.(作图工具不限,不写作法,但要有必要的说明)
(3)判断下列命题的真假,在括号内填“真”或“假”.
①任意凸四边形一定存在准内点.( )
②任意凸四边形一定只有一个准内点.( )
③若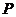 是任意凸四边形
是任意凸四边形 的准内点,则
的准内点,则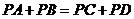
或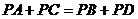 .(
)
.(
)
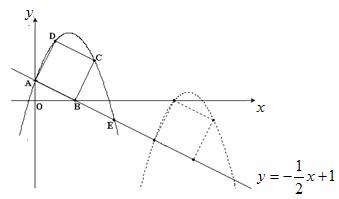
24.如图,已知直线 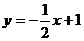 交坐标轴于
交坐标轴于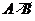 两点,以线段
两点,以线段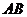 为边向上作
为边向上作
正方形 ,过点
,过点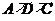 的抛物线与直线另一个交点为
的抛物线与直线另一个交点为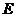 .
.
(1)请直接写出点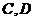 的坐标;
的坐标;
(2)求抛物线的解析式;
(3)若正方形以每秒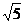 个单位长度的速度沿射线
个单位长度的速度沿射线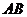 下滑,直至顶点
下滑,直至顶点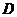 落在
落在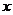 轴上时停止.设正方形落在
轴上时停止.设正方形落在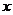 轴下方部分的面积为
轴下方部分的面积为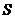 ,求
,求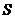 关于滑行时间
关于滑行时间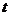 的函数关系式,并写出相应自变量
的函数关系式,并写出相应自变量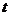 的取值范围;
的取值范围;
(4)在(3)的条件下,抛物线与正方形一起平移,同时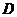 停止,求抛物线上
停止,求抛物线上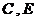 两点间的抛物线弧所扫过的面积.
两点间的抛物线弧所扫过的面积.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com