
高 二 数 学 水 平 测 试 卷
考生注意:1)本试卷共八个大题,满分150分,考试时间120分钟;
2)内容:高一(上、下),高二(上、下);
3)考生需写出必要的推理、演算过程,否则记为0分;
4)将解答写在答题纸上,并标明题号,在试卷上作答无效。
一.本题共5个小题,每题7分,共35分。
1. 已知集合A={1,2,3},集合B={4,5},定义A*B=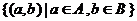 ,
,
写出A*B中的所有元素。
2. 已知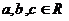 ,函数
,函数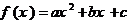 ,并且当
,并且当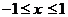 时,
时,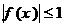 ,证明:
,证明: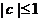
3. 求n的值: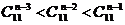
4. 求和: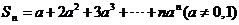
5.求证: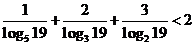
二.(15分)在 中,角A,B,C所对的边分别为a,b,c,且
中,角A,B,C所对的边分别为a,b,c,且 ,
,
1)求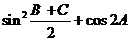 的值;(7分)
的值;(7分)
2)若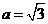 ,求bc的最大值。(8分)
,求bc的最大值。(8分)
1)求P点的轨迹是什么曲线?(8分)
三.(15分)已知两点M(--1,0),N(1,0),且点P使 ,
, ,
, 成公差小于零的等差数列
成公差小于零的等差数列
2)若点P的坐标为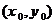 ,记
,记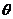 为
为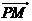 与
与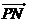 的夹角,求
的夹角,求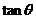 。(7分)
。(7分)
求 1)A,B两组中有一组恰有2支弱队的概率(8分)
2)A组中至少有2支弱队的概率。(7分)
四.(15分)已知8支球队共有3支弱队,以抽签方式将这8支球队分为A,B两组,每组4支
五.(15分)已知数列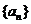 的前n项和
的前n项和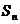 满足
满足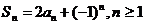
1)写出数列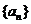 的前三项
的前三项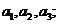 (7分)
(7分)
2)求数列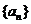 的通项公式。(8分)
的通项公式。(8分)
六.(15分)已知椭圆 ,椭圆上有不同的三点A,B,C且
,椭圆上有不同的三点A,B,C且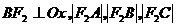 成等差数列
成等差数列
(1)求弦AC的中点M的横坐标;
(2)设弦AC的垂直平分线的方程为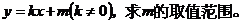
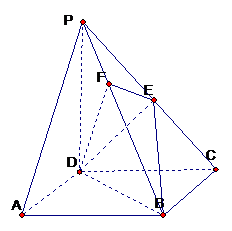
七.(20分)如图,在四棱锥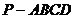 中,底面ABCD是正方形,侧棱
中,底面ABCD是正方形,侧棱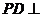 底面ABCD,
底面ABCD,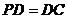 ,E是PC的中点,作
,E是PC的中点,作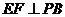 交PB于点F。
交PB于点F。
1)证明 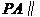 平面
平面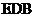 ;(6分)
;(6分)
2)证明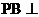 平面EFD; (7分)
平面EFD; (7分)
3)求二面角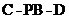 的大小。(7分)
的大小。(7分)
八.(20分)设函数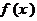 的定义域为R,对任意实数m, n总有
的定义域为R,对任意实数m, n总有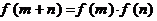 ,且x>0时,
,且x>0时,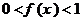 。
。
1)证明: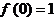 ,且
,且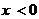 时,
时,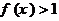 ;(7分)
;(7分)
2)证明: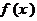 在R上单调递减;(6分)
在R上单调递减;(6分)
3)设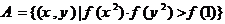 ,
,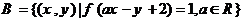 ,若
,若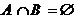 ,确定a的取值范围。(7分)
,确定a的取值范围。(7分)
答 案
一.本题共5个小题,每题7分,共35分。
1.已知集合A={1,2,3},集合B={4,5},定义A*B=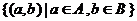 ,
,
写出A*B中的所有元素。
答:(1,4),(1,5),(2,4),(2,5),(3,4),(3,5)
2.已知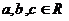 ,函数
,函数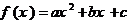 ,并且当
,并且当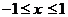 时,
时,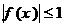 ,证明:
,证明: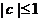
证明:因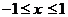 时,
时,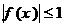 ,所以当x=0时,有
,所以当x=0时,有 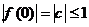
3.求n的值: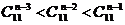
解: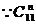 中最大的为
中最大的为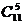 ,
,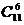 ,
, 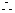 有
有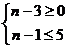 于是
于是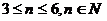
所以n=3,4,5,6
4. 求和: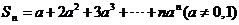
解: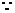
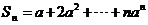
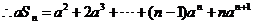
于是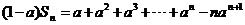
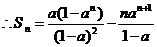
5.求证: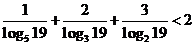
证明: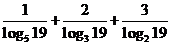
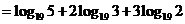
=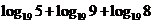 =
=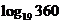 <
<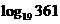 =2
=2
二.(15分)在 中,角A,B,C所对的边分别为a,b,c,且
中,角A,B,C所对的边分别为a,b,c,且 ,
,
1)求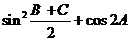 的值;(7分)
的值;(7分)
2)若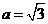 ,求bc的最大值。(8分)
,求bc的最大值。(8分)
解:1)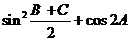 =
=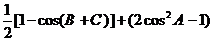
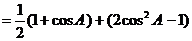
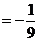
2)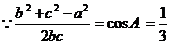
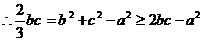
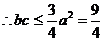
当且仅当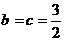 时,bc取最大值
时,bc取最大值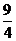
1)求P点的轨迹是什么曲线?(8分)
三.(15分)已知两点M(--1,0),N(1,0),且点P使 ,
, ,
, 成公差小于零的等差数列
成公差小于零的等差数列
2)若点P的坐标为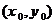 ,记
,记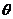 为
为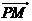 与
与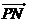 的夹角,求
的夹角,求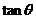 。(7分)
。(7分)
解:1)记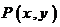 ,则有
,则有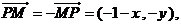
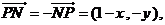
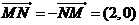
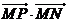 =2(1+x),
=2(1+x),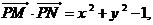
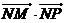 =2(1―x)
=2(1―x)
由题意得: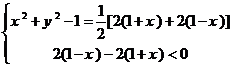
即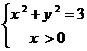 所以P点轨迹是以原点为圆心,
所以P点轨迹是以原点为圆心,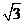 为半径的右半圆
为半径的右半圆
2)点P的坐标为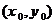 ,而
,而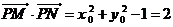 ,
,
又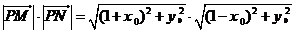 =
= 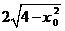
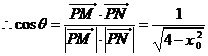 ,
,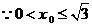 ,
,
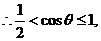
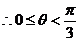 于是
于是
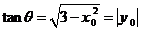
求 1)A,B两组中有一组恰有2支弱队的概率(8分)
2)A组中至少有2支弱队的概率。(7分)
四.(15分)已知8支球队共有3支弱队,以抽签方式将这8支球队分为A,B两组,每组4支
解:1)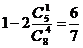 或
或 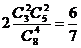
2)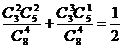
五.(15分)已知数列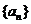 的前n项和
的前n项和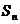 满足
满足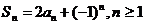
1)写出数列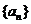 的前三项
的前三项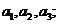 (7分)
(7分)
2)求数列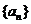 的通项公式。(8分)
的通项公式。(8分)
解:1)由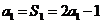 ,得
,得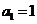
由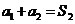 =
=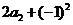 ,得
,得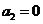
由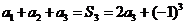 ,得
,得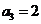
2)当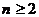 时,有
时,有
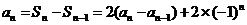
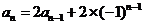
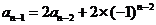 ,
,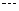 ,
,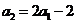
所以 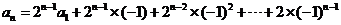
=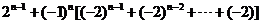
=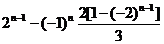 =
=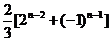
经验证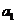 也满足上式,所以
也满足上式,所以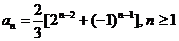
六.(15分)已知椭圆 ,椭圆上有不同的三点A,B,C且
,椭圆上有不同的三点A,B,C且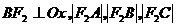 成等差数列
成等差数列
(1)求弦AC的中点M的横坐标;
(2)设弦AC的垂直平分线的方程为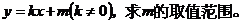
解:(1)由题意可得,
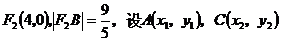 ,由焦半径公式,得
,由焦半径公式,得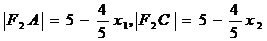
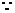
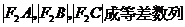
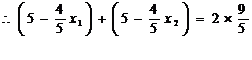
由此有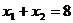
故弦AC的中点的横坐标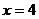
(2)将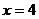 代入
代入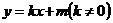 ,故点M的坐标为(
,故点M的坐标为(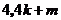 ),则
),则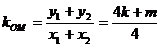 ,又
,又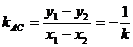
由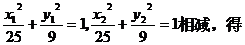
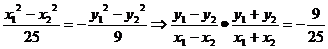
即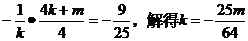
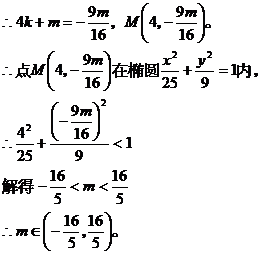
七.(20分)如图,在四棱锥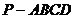 中,底面ABCD是正方形,侧棱
中,底面ABCD是正方形,侧棱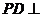 底面ABCD,
底面ABCD,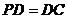 ,E是PC的中点,作
,E是PC的中点,作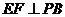 交PB于点F。
交PB于点F。
1)证明 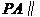 平面
平面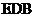 ;(6分)
;(6分)
2)证明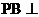 平面EFD; (7分)
平面EFD; (7分)
3)求二面角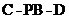 的大小。(7分)
的大小。(7分)
(方法一):
1. 证明:连结AC,AC交BD于O。连结EO。
|