
高三数学(文)
本卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分150分,考试时间120分钟。
注意事项:
1.答第I卷前,考生务必将自己的姓名、准考证号、考试科目涂写在答题卡上。
2.第I卷每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号。
3.考试结束后,监考人员将本试卷和答题卡一并收回。
参考公式:
如果事件A、B互斥,那么
球的表面积公式: :球的体积公式:
:球的体积公式: ,其中R表示球的半径。
,其中R表示球的半径。
锥体体积公式: ;柱体体积公式:
;柱体体积公式: ,其中
,其中 是底面积,
是底面积, 是几何体的高。
是几何体的高。
第I卷(共50分)
一、选择题:本大题共10小题,每小题5分,共50分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合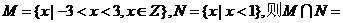
A.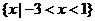 B.
B.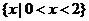
C.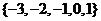 D.
D.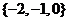
2.要得到函数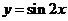 的图象,只需将函数
的图象,只需将函数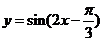 的图象
的图象
A.向右平移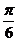 个单位长度 B.向左平移
个单位长度 B.向左平移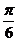 个单位长度
个单位长度
C.向右平移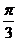 个单位长度 D.向左平移
个单位长度 D.向左平移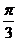 个单位长度
个单位长度
3.过抛物线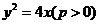 的焦点作直线交抛物线于
的焦点作直线交抛物线于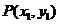 、
、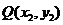 两点,若
两点,若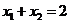 ,则
,则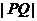 等于
等于
A.4
B.
4.若平面向量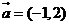 与
与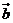 的夹角是180°,且
的夹角是180°,且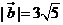 ,则
,则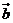 的坐标为
的坐标为
A.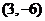 B.
B.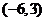 C.
C.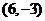 D.
D.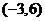
5.如果不等式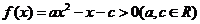 的解集为
的解集为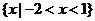 ,那么函数
,那么函数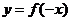 的大致图象是
的大致图象是
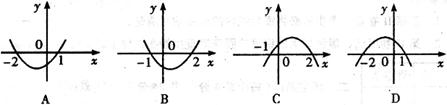
6.设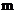 、
、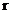 是两条不同的直线,
是两条不同的直线,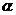 、
、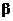 为两个不同的平面, 则下列四个命题中不正确的是
为两个不同的平面, 则下列四个命题中不正确的是
A.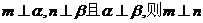 B.
B.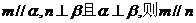
C.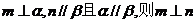 D.
D.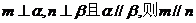
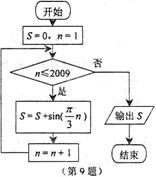
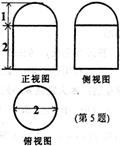 7.右图是一个几何体的三视图,根据图中数据,可得该几何题的表面积是
7.右图是一个几何体的三视图,根据图中数据,可得该几何题的表面积是
A.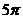
B.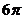
C.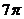
D.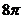
 B.56
B.56
C.60
D.62
9.直线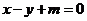 与圆
与圆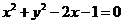 有两个不同交点的一个充分不必要条件是
有两个不同交点的一个充分不必要条件是
A.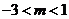 B.
B.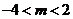
C.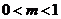 D.
D.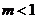
10.函数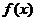 满足
满足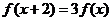 ,且
,且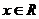 ,当
,当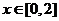 时,
时,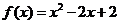 ,则
,则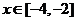 时,
时,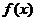 的最小值为
的最小值为
A.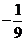 B.
B.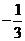 C.
C.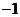 D.
D.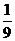
第Ⅱ卷 非选择题(共100分)
注意事项:
1.答第Ⅱ卷前,考生务必将密封线内的项目填写清楚。
2.第Ⅱ卷用蓝、黑色墨水的钢笔或圆珠笔直接答在试卷上。
 二、填空题:(每小题4分,共24分)
二、填空题:(每小题4分,共24分)
11.如过复数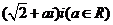 的实部与虚部是互为相反数,则
的实部与虚部是互为相反数,则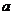 的值等于_________。
的值等于_________。
12.统计某校1000名学生的数学学业水平测试成绩,得到样本频率分布直方图如右图,规定不低于60分为及格,不低于80分为优秀,则及格人数是_______,优秀率为________。
13.已知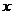 、
、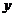 满足约束条件
满足约束条件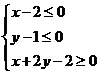
则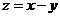 的最大值为_______________。
的最大值为_______________。
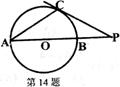 14.如图,
14.如图,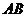 是⊙
是⊙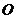 的直径,
的直径,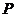 是
是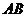 延长线上的一点。过
延长线上的一点。过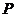 作⊙
作⊙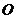 的切线,切点为
的切线,切点为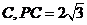 ,若
,若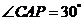 ,则⊙
,则⊙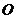 的直径
的直径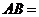 ____________。
____________。
15.若函数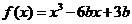 在(
在(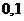 )内有极小值,则实数
)内有极小值,则实数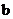 的取值范围是_______。
的取值范围是_______。
16.观察下表:
1
2 3 4
3 4 5 6 7
4 5 6 7 8 9 10
…………
则第__________行的各数之和等于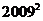 。
。
三、解答题:(17~20题,每小题12分,第21、22题14分,共计76分)
17.(本题满分12分)
已知在锐角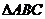 中,角
中,角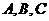 对边分别为
对边分别为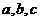 且
且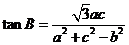
(1)求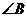 ;
;
(2)求函数 的最小正周期及单调递减区间;
的最小正周期及单调递减区间;
18.(本题满分12分)
如图,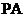 垂直于矩形
垂直于矩形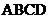 所在的平面,
所在的平面,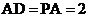 ,
,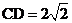 ,
,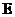 、
、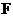 分别
分别
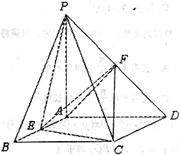 是
是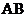 、
、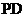 的中点。
的中点。
(I)求证: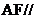 平面
平面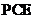 ;
;
(Ⅱ)求证:平面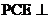 平面
平面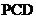 ;
;
(Ⅲ)求四面体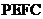 的体积
的体积
19.(本题满分12分)
现有编号分别为1,2,3的三个不同的政治基本题和一道政治附加题:另有编号分别为
4,5的两个不同的历史基本题和一道历史附加题。甲同学从这五个基本题中一次随即抽取两道题,每题做对做错及每题被抽到的概率是相等的。
(1)用符号(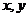 )表示事件“抽到的两题的编号分别为
)表示事件“抽到的两题的编号分别为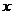 、
、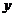 ,且
,且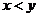 ”共有多少个基本事件?请列举出来:
”共有多少个基本事件?请列举出来:
(2)求甲同学所抽取的两道基本题的编号之和小于8但不小于4的概率。
(3)甲同学在抽完两道基本题之后又抽取一道附加题,做对基本题每题加5分,做对政治附加题加10分,做对历史附加题加15分,求甲同学得分不低于20分的概率。
20.(本题满分12分)
已知函数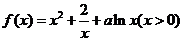 ,
,
(1)令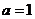 ,求函数
,求函数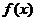 在
在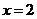 处的切线方程;
处的切线方程;
(2)若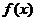 在
在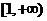 上单调递增,求
上单调递增,求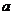 的取值范围。
的取值范围。
21.(本题满分14分)
设数列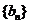 的前
的前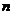 项和为
项和为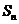 ,且
,且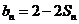 ;数列
;数列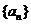 为等差数列,且
为等差数列,且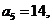
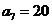 。
。
(1)求数列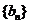 的通项公式;
的通项公式;
(2)若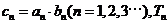 为数列
为数列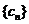 的前
的前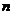 项和,求证:
项和,求证: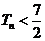 。
。
22.(本题满分14分)
已知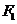 、
、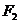 分别是椭圆
分别是椭圆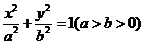 的左、右焦点,右焦点
的左、右焦点,右焦点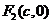 到上顶点的距离为2,若
到上顶点的距离为2,若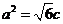
(1)求此椭圆的方程;
(2)点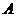 是椭圆的右顶点,直线
是椭圆的右顶点,直线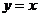 与椭圆交于
与椭圆交于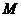 、
、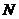 两点(
两点(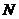 在第一象限内),又
在第一象限内),又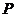 、
、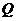 是此椭圆上两点,并且满足
是此椭圆上两点,并且满足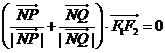 ,求证:向量
,求证:向量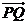 与
与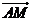 共线
共线
一、选择题:本大题共10小题,每小题5分,共50分。在每小题给出的四个选项中,只有一项是符合题目要求的。
题号
1
2
3
4
5
6
7
8
9
10
答案
D
B
A
A
C
B
C
B
C
D
二、填空题:(每小题4分,共24分)
11. 12.800,20% 13.2 14.4 15.
12.800,20% 13.2 14.4 15. 16.1005
16.1005
三、解答题:(17~20题,每小题12分,第21、22题14分,共计76分)
17.(本题满分12分)
解:(1)在 中,利用余弦定理,
中,利用余弦定理, ,
,
代入 得,
得,
而 是锐角三角形,所以角
是锐角三角形,所以角 ??????????????????????? 5分
??????????????????????? 5分
(2)
周期
因为
所以 ????????????????????????? 8分
????????????????????????? 8分
当 时,
时, 又
又 ;
;
所以, 在
在 上的单调减区间为
上的单调减区间为 ???????? 12分
???????? 12分
18.(本题满分12分)
解(I)设 为
为 的中点,连结
的中点,连结 ,
,
 为
为 的中点,
的中点, 为
为 的中点,
的中点,
 ==
==  ==
==
 ==
==

 ????????????????????????????????????????????????? 4分
????????????????????????????????????????????????? 4分
 (Ⅱ)
(Ⅱ)


(Ⅲ)由(Ⅱ)知 ,
,

19.(本题满分12分)
解:(1)共有10个等可能性的基本事件,列举如下:(1,2),(1,3),(1,4),(1,5),
(2,3),(2,4),(2,5)(3,4),(3,5),(4,5)。
(2)记事件“甲同学所抽取的两题的编号之和小于8但不小于4”为事件A
由(1)可知事件共含有7个基本事件,列举如下:(1,3),(1,4),(1,5),(2,3),
(2,4),(2,5),(3,4)
(3)记事件B“做对政治附加题同时还需做对两道基本题”
记事件C“做对历史附加题同时还需至少做对一道基本题”
记事件D“甲同学得分不低于20分”

20.(本题满分12分)
(1)与由
切线的斜率 切点坐标
切点坐标
所求切线方程 ?????????????????????????????? 5分
?????????????????????????????? 5分
(2)若函数为 上单调增函数,
上单调增函数,
则 上恒成立,即不等式
上恒成立,即不等式 在
在 上恒成立。
上恒成立。
也即 在
在 上恒成立
上恒成立
令 ,上述问题等价于
,上述问题等价于
而 为在
为在 上的减函数,
上的减函数,
则 ,于是
,于是 为所求????????????????????????? 12分
为所求????????????????????????? 12分
21.(本题满分14分)
解(1)由


(2)数列 为等差数列,公差
为等差数列,公差
从而

从而
22.(本题满分14分)
解:(1)由题知: ????? 4分
????? 4分
(2)因为: ,从而
,从而 与
与 的平分线平行,
的平分线平行,
所以 的平分线垂直于
的平分线垂直于 轴;
轴;
由
不妨设 的斜率为
的斜率为 ,则
,则 的斜率
的斜率 ;因此
;因此 和
和 的方程分别为:
的方程分别为:
 、
、 ;其中
;其中 ;?????????? 8分
;?????????? 8分
由 得;
得;
因为 在椭圆上;所以
在椭圆上;所以 是方程
是方程 的一个根;
的一个根;
从而; ????????????????????????????????????????? 10分
????????????????????????????????????????? 10分
同理: ;从而直线
;从而直线 的斜率
的斜率 ;
;
又 、
、 ;所以
;所以 ;所以
;所以 所以向量
所以向量 与
与 共线。 14分www.ks5u.com
共线。 14分www.ks5u.com
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com