
2009年云南省曲靖一中高考冲刺卷 理科数学(三)
理科数学(三)
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分150分,考试时间120分钟.
第Ⅰ卷(选择题,共60分)
一、选择题:本大题共12小题.每小题5分,共60分.在每小题给出的四个选项中.只 
有一项是符合题目要求的.
1.设集合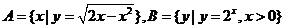 ,则
,则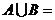

A.(1,2] B.[0,+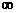 )
)
C.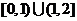 D.[0,2]
D.[0,2]
2.设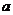 是实数,且
是实数,且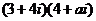 是纯虚数,则
是纯虚数,则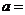

A.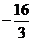 B.
B.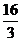 C.
C.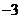 D.3
D.3
3.若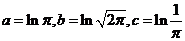 ,则
,则
A.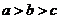 B.
B.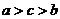 C.
C.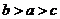 D.
D.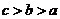

4.若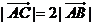 ,且
,且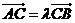 ,则
,则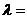

A.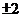 B.
B.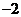 C.
C.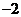 或
或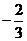 D.
D.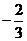

5.在等差数列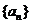 中,有
中,有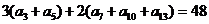 ,则此数列的前13项之和为
,则此数列的前13项之和为
A.24 B.
6.设曲线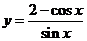 在点
在点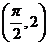 处的切线与直线
处的切线与直线 垂直,则
垂直,则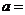

A.2 B.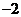 C.
C.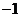 D.1
D.1
7.若直线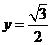 与函数
与函数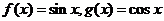 分别相交于相邻的
分别相交于相邻的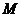 、
、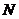 两点,则
两点,则
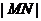 的最大值为
的最大值为
A.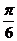 B.
B.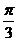 C.
C.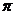 D.
D.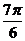

8.设偶函数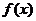 在
在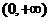 上为减函数,且
上为减函数,且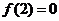 ,则不等式
,则不等式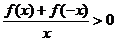 解集
解集
为
A.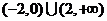 B.
B.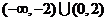

C.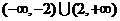 D.
D.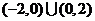

9.若函数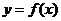 的图象与函数
的图象与函数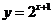 的图象关于
的图象关于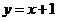 对称,则
对称,则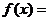

A.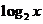 B.
B.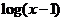

C.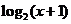 D.
D.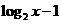

10.高考资源网若直线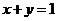 通过点
通过点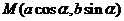 ,则
,则
A.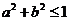 B.
B.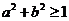

C.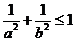 D.
D.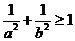

11.高考资源网已知四棱柱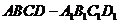 的底面为正方形,侧棱与底面边长相等,
的底面为正方形,侧棱与底面边长相等,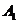 在底面
在底面
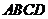 内的射影为正方形
内的射影为正方形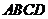 的中心,则
的中心,则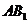 与底面
与底面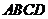 所成角的正弦值等于
所成角的正弦值等于
A.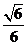 B.
B.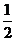 C.
C.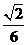 D.
D.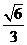

12.将正方体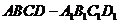 的各面涂色,任何相邻两个面不同色,现在有5种不同的
的各面涂色,任何相邻两个面不同色,现在有5种不同的
颜色,并且涂好了过顶点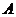 的3个面的颜色,那么其余的3个面的涂色的方案共有
的3个面的颜色,那么其余的3个面的涂色的方案共有
A.15种 B.14种 C.13种 D.12种

第Ⅱ卷(非选择题,共90分)
二、填空题:本大题共4小题,每小题5分,共20分.把答案填在题中横线上.
13.若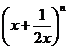 的展开式中前三项的系数成等差数列,则展开式中
的展开式中前三项的系数成等差数列,则展开式中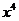 项的系数为
项的系数为 
(用数字作答).
14.若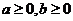 ,且当
,且当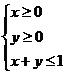 时.恒有
时.恒有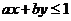 ,则以
,则以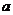 、
、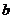 为坐标的点
为坐标的点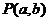 所
所
形成的平面区域的面积是
.
15.设焦点在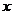 轴上的双曲线
轴上的双曲线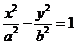 的右准线与两条渐近线交于
的右准线与两条渐近线交于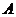 、
、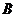 两点,右焦点
两点,右焦点
为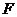 ,且
,且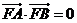 ,则双曲线的离心率
,则双曲线的离心率 .
.
16.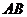 垂直于
垂直于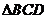 所在的平面,
所在的平面,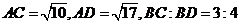 ,当
,当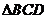 的
的
面积最大时,点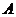 到直线
到直线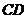 的距离为
.
的距离为
.
三、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分10分)
若函数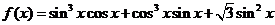 .
.
(1)求函数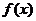 的单调递减区间;
的单调递减区间;
(2)已知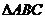 的三边
的三边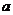 、
、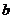 、
、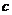 对应角为
对应角为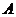 、
、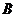 、
、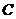 ,且三角形的面积为
,且三角形的面积为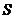 ,若
,若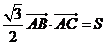 ,求
,求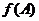 的取值范围.
的取值范围.
18.(本小题满分12分)
因金融危机,某公司的出口额下降,为此有关专家提出两种促进出口的方案,每种方案都需要分两年实施.若实施方案一,预计第一年可以使出口额恢复到危机前的1.0倍、0.9倍、0.8倍的概率分别为0.3、0.3、0.4;第二年可以使出口额为第一年的1.25倍、1.0倍的概率分别是0.5、0.5.若实施方案二,预计第一年可以使出口额恢复到危机前的1.2倍、l.0倍、0.8倍的概率分别为0.2、0.3、0.5;第二年可以使出口额为第一年的1.2倍、1.0倍的概率分别是0.4、0.6.实施每种方案第一年与第二年相互独立.令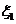 (
(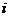 =1,2)表示方案
=1,2)表示方案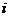 实施两年后出口额达到危机前的倍数。
实施两年后出口额达到危机前的倍数。
(1)写出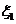 、
、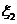 的分布列;
的分布列;
(2)实施哪种方案,两年后出口额超过危机前出口额的概率更大?
(3)不管哪种方案,如果实施两年后出口额达不到、恰好达到、超过危机前出口额,预计利润分别为10万元、15万元、20万元,问实施哪种方案的平均利润更大?
19.(本小题满分12分)
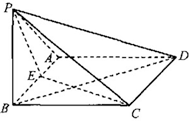 四棱锥
四棱锥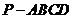 中,底面
中,底面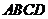 为矩形,侧面
为矩形,侧面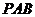 为正三角形,
为正三角形,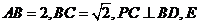 为
为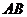 的中点.
的中点.
(1)证明: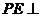 平面
平面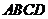 ;
;
(2)求二面角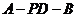 的大小.
的大小.
20.(本小题满分12分)
已知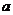 、
、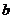 、
、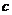 均为正整数,且
均为正整数,且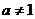 ,等差数列
,等差数列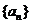 的首项为
的首项为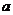 ,公差为
,公差为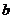 ,等比数列
,等比数列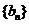 的首项为
的首项为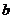 ,公比为
,公比为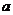 ,且
,且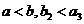 ,在数列
,在数列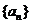 和
和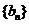 中各存在一项
中各存在一项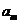 与
与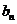 ,使得
,使得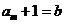 ,又
,又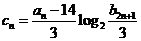 .
.
(1)求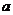 、
、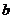 的值;
的值;
(2)求数列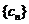 中的最小项,并说明理由.
中的最小项,并说明理由.
21.(本小题满分12分)
椭圆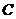 的中心为坐标原点
的中心为坐标原点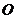 ,焦点在
,焦点在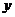 轴上,焦点到相应准线的距离以及离心率均为
轴上,焦点到相应准线的距离以及离心率均为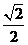 ,直线
,直线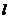 与
与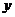 轴交于点
轴交于点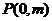 ,与椭圆
,与椭圆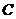 交于相异两点
交于相异两点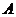 、
、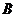 ,且
,且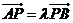 .
.
(1)求椭圆方程;
(2)若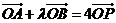 ,求
,求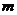 的取值范围.
的取值范围.
22.(本小题满分12分)
已知函数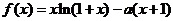 ,其中
,其中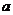 为常数.
为常数.
(1)当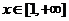 时,
时,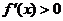 恒成立,求
恒成立,求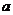 的取值范围;
的取值范围;
(2)求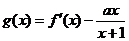 的单调区间.
的单调区间.
1.B 2.D 3.A 4.C 5.C 6.D 7.D 8.B 9.C 10.B
11.A 12.C
1. ,所以选B.
,所以选B.
2. ,所以选D.
,所以选D.
3. ,所以选
,所以选 .
.
4. 或
或 ,所以选C.
,所以选C.
5. ,所以选C.
,所以选C.
6. ,切线斜率
,切线斜率
 ,所以选D.
,所以选D.
7.观察图象 .所以选D.
.所以选D.
8.化为 或
或 ,所以选B.
,所以选B.
9. 与
与 关于
关于 对称,
对称, ,所以选C.
,所以选C.
10.直线 与椭圆
与椭圆 有公共点
有公共点 ,所以选B.
,所以选B.
11.如图,设 ,则
,则 ,
,

 ,
,
 ,从而
,从而 ,因此
,因此 与底面所成角的正弦值等于
与底面所成角的正弦值等于 .所以选A.
.所以选A.
12.分类涂色①
只用3种颜色,相对面同色,有1种涂法;② 用4种颜色,有 种涂法;③ 用五种颜色,有
种涂法;③ 用五种颜色,有 种涂法.共有13种涂法.所以选C.
种涂法.共有13种涂法.所以选C.
二、
13.7.由 或
或 (舍去),
(舍去),
 项的余数为
项的余数为 .
.
14.依题设 ,又
,又 ,点
,点 所形成的平面区域为边长为1的正方形,其面积为1.
所形成的平面区域为边长为1的正方形,其面积为1.
15. ,由
,由 ,得
,得
 .
.
16. .
.

如图,可设 ,又
,又 ,
,
 .
.
当 面积最大时,
面积最大时, .点
.点 到直线
到直线 的距离为
的距离为 .
.
三、
17.(1)

由
 得
得 ,
,
 的单调递减区间为
的单调递减区间为 .
.
(2)



 .
.
18.(1) 的所有取值为0.8,0.9,1.0,1.125,1.25,其分布列为
的所有取值为0.8,0.9,1.0,1.125,1.25,其分布列为

0.8
0.9
1.0
1.125
1.25

0.2
0.15
0.35
0.15
0.15
 的所有取值为0.8,0.96,1.0,1,2,1.44,其分布列为
的所有取值为0.8,0.96,1.0,1,2,1.44,其分布列为

0.8
0.96
1.0
1.2
1.44

0.3
0.2
0.18
0.24
0.08
(2)设实施方案一、方案二两年后超过危机前出口额的概率为 ,
, ,则
,则

∴实施方案二两年后超过危机前出口额的概率更大.
(3)方案一、方案二的预计利润为 、
、 ,则
,则

10
15
20

0.35
0.35
0.3

10
15
20

0. 5
0.18
0.32


∴实施方案一的平均利润更大
19.(1)设 与
与 交于点
交于点 .
.



从而 ,即
,即 ,又
,又 ,且
,且
 平面
平面 为正三角形,
为正三角形, 为
为 的中点,
的中点,
 ,且
,且 ,因此,
,因此, 平面
平面 .
.
(2) 平面
平面 ,∴平面
,∴平面 平面
平面 又
又 ,∴平面
,∴平面 平面
平面
设 为
为 的中点,连接
的中点,连接 ,则
,则 ,
,
 平面
平面 ,过点
,过点 作
作 ,连接
,连接 ,则
,则 .
.
 为二面角
为二面角 的平面角.
的平面角.
在 中,
中, .
.
又 .
.
20.(1)由 ,得
,得 ,则
,则
又 为正整数,
为正整数,

 ,故
,故 .
.
(2)

∴当 或
或 时,
时, 取得最小值
取得最小值 .
.
21.(1)由 得
得
∴椭圆 的方程为:
的方程为: .
.
(2)由 得
得 ,
,

又
设直线 的方程为:
的方程为:
由 得
得


由此得 . ①
. ①
设 与椭圆
与椭圆 的交点为
的交点为 ,则
,则
www.ks5u.com由 得
得
 ,整理得
,整理得
 ,整理得
,整理得
 时,上式不成立,
时,上式不成立, ②
②
由式①、②得
 或
或
∴ 取值范围是
取值范围是 .
.
22.(1)由 得
得
令 ,则
,则
当 时,
时, 在
在 上单调递增.
上单调递增.

 的取值范围是
的取值范围是 .
.
(2)
则
① 当 时,
时, 是减函数.
是减函数.
 时,
时, 是增函数.
是增函数.
② 当 时,
时, 是增函数.
是增函数.
综上;当 时,增区间为
时,增区间为 ,,减区间为
,,减区间为 ;
;
当 时,增区间为
时,增区间为 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com