北京东城区
2008―2009学年度高三第二学期统一练习(二)
数学试题(文科)
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分。考试时间120分钟。考试结束,将本试卷和答题卡一并交回。
第Ⅰ卷(选择题 共40分)
注意事项:
1.答第Ⅰ卷前,考生务必将自己的姓名、准考证号、考试科目写在答题卡上.
2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.不能答在试卷上.
一、选择题:本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.
1.已知集合 为 ( )
为 ( )
A.{0,1} B.{0,2} C.{1,2} D.{0,1,2}
试题详情
2.已知函数 的解集是 ( )
的解集是 ( )
试题详情
A. B.(0,1) C.(1,2) D.
B.(0,1) C.(1,2) D.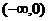
试题详情
3.若圆C与圆 关于原点对称,则圆C的方程为 ( )
关于原点对称,则圆C的方程为 ( )
试题详情
A. B.
B.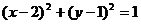
试题详情
C. D.
D.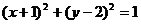
试题详情
4.若 的展开式的二项式系数之和为128,则n的值为 ( )
的展开式的二项式系数之和为128,则n的值为 ( )
A.6 B.7 C.8 D.9
试题详情
5.下列函数中既是奇函数,又在区间 上单调递增的是 ( )
上单调递增的是 ( )
试题详情
试题详情
6.若 的终边在 ( )
的终边在 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
试题详情
7.已知直线 和两个平面
和两个平面 ,给出下列四个命题:
,给出下列四个命题:
试题详情
①若 内的任何直线都与
内的任何直线都与 平行;
平行;
试题详情
②若 内的任何直线都与
内的任何直线都与 垂直;
垂直;
试题详情
③若 内的任何直线都与
内的任何直线都与 平行;
平行;
试题详情
④若 内的任何直线都与
内的任何直线都与 垂直;
垂直;
则其中 ( )
A.②、③为真 B.①、②为真
C.①、③为真 D.③、④为真
试题详情
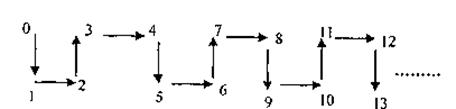
则根据规律,从2007到2009,箭头的方向是 ( )
试题详情
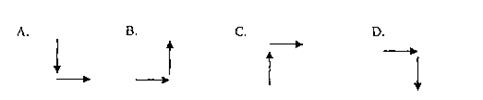
第Ⅱ卷(共110分) 注意事项:
试题详情
试题详情
试题详情
二、填空题:本大题共6小题,每小题5分,共30分.把答案填写在题中横线上. 9.在总体为N的一批零件中抽取一个容量为30的样本,若每个零件被抽取的可能性为25%,则N的值为
。 试题详情
10.双曲线 的渐近线的方程为
;渐近线与准线的夹角是
。 的渐近线的方程为
;渐近线与准线的夹角是
。 试题详情
11.已右 是大于2的整数,则 是大于2的整数,则 的值为
。 的值为
。
|
试题详情
13.某校学生会由高一年级的4名学生、高二年级的5名学生、高三年级的4名学生组成,现从学生会中选出2名学生,参加一次活动,则此2名学生不属于同一个年级的选出方法共有
种。 试题详情
14.已知点P在直线 上,PQ中点为 上,PQ中点为 的取值范围是
。 的取值范围是
。 试题详情
三、解答题:本大题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程.
试题详情
已知函数 试题详情
(1)求函数 的解析式; 的解析式; 试题详情
(2)设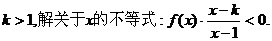 试题详情
试题详情
已知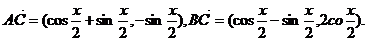 试题详情
(1)设 的最小正周期和单调递减区间; 的最小正周期和单调递减区间; 试题详情
(2)设有不相等的两个实数 的值。 的值。 试题详情
试题详情
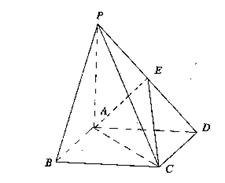
(1)证明:PB//平面AEC; (2)求二面角E―AC―D的大小。
试题详情
试题详情
已知函数 的图象都过 的图象都过 ,且在点P处有相同的切线。 ,且在点P处有相同的切线。 试题详情
(1)求实数 的值; 的值; 试题详情
(2)设函数 在区间[-3,0]上的最大值和最小值。 在区间[-3,0]上的最大值和最小值。 试题详情
试题详情
在一次抗洪抢险中,准备用射击的方法引爆从河上游漂流而下的一只巨大汽油罐,已知只有5发子弹备用,且首次命中只能使汽油流出。再次命中才能引爆成功,每次射击命中的概率都是 ,每次命中与否互相独立。 ,每次命中与否互相独立。 (1)求恰用3发子弹就将油罐引爆的概率; (2)求油罐被引爆的概率。 试题详情
试题详情
试题详情
(1)求点 的坐标; 的坐标; 试题详情
试题详情
一、选择题(本大题共8小题,每小题5分,共40分) 1―4DBAB 5―8CBAD 二、填空题(本大题共6小题,每小题5分,有两空的小题,第一空3分,第二空2分,共30分)
20090508 10. 11.36 12. 13.56 14. 注:两个空的填空题第一个空填对得3分,第二个空填对得2分。 三、解答题(本大题共6小题,共80分) 15.(本小题共13分) 解:(1)依题意函数 有 故 4分 4分 (2)由 原不等式等价于  6分 6分 当 时, 时, 8分 8分 当 时, 时, 10分 10分 当 时, 时,  此时不等式组无解 12分 所以,当 时,不等式的解集为 时,不等式的解集为 当 时,不等式的解集为 时,不等式的解集为 当 时,不等式的解集为空集。 13分 时,不等式的解集为空集。 13分 16.(本小题满分13分) 解:(1)由 得 得  4分 4分   6分 6分 所以 8分 8分 又由 得 故 单调递减区间是 单调递减区间是  10 10 (2)由 故 12分 12分 又 得 12分 12分 所以 13分 13分 17.(本小题满分14分)

 为BD中点,E为PD中点, 为BD中点,E为PD中点,  3分 3分  平面AEC,PB 平面AEC,PB 平面AEC, 平面AEC,  PB//平面AEC。 6分 PB//平面AEC。 6分 (2)解法一:取AD中点L, 过L作 于K,连结EK,EL, 于K,连结EK,EL,  L为AD中点, L为AD中点,  EL//PA, EL//PA,

 LK为EK在平面ABCD内的射影。 LK为EK在平面ABCD内的射影。 又  为二面角E―AC―D的平面角 10分 为二面角E―AC―D的平面角 10分 在  ∽ ∽  设正方形边长为2, 则 12分 12分 在  二面角E―AC―D的大小为 二面角E―AC―D的大小为 14分 14分 解法二: (2)如图,以A为坐标原点,AB,AD,AP所在直线分别为

由 ,设正方形边长为2, ,设正方形边长为2, 则 (0,0,0), (0,0,0), (2,0,0), (2,0,0), (2,2,0), (2,2,0),  (0,2,0),P(0,0,2),E(0,1,1)10分 (0,2,0),P(0,0,2),E(0,1,1)10分 ∵ ⊥平面 ⊥平面 , , ∴ 是平面 是平面 的法向量, 的法向量, =(0,0,2), =(0,0,2), 设面AEC的法向量为  则 令 ,则 ,则 (1,-1,1) 12分 (1,-1,1) 12分  = = 。 。 ∴二面角 的大小为arccos 的大小为arccos 。 14分 。 14分 18.(本小题满分13分) 解:(1) , 2分 , 2分 根据题意有 4分 4分 解得 6分 6分 (2)由(1)知 则 7分 7分  8分 8分 令 ,即 ,即 解得 解得 或 或 11分 11分 令 ,即 ,即 解得 解得 当 在[-3,0]内变化时, 在[-3,0]内变化时, 与 与 的变化情况如下: 的变化情况如下: 
-3 (-3,-2) -2 (-2,0) 0 
+ + 0 - - 
-10 ㄊ 极大值 ㄋ -16 当 时, 时, 有最小值-16;当 有最小值-16;当 时, 时, 有最大值0 13分 有最大值0 13分 19.(本小题满分13分) 解:(1)恰用3发子弹就将油罐引爆记为事件A,则 即恰用3发子弹将油罐引爆的概率为 6分 6分 (2)记“油罐被引爆”的事件为事件B,其对立事件为 则 10分 10分 故 即油罐被引爆的概率为 13分 13分 20.(本小题满分14分) 解:(1)由 的横坐标成以 的横坐标成以 为首项,-1为公差的等差数列 为首项,-1为公差的等差数列 , , 故 。 3分 。 3分 又 位于函数 位于函数 的图象上, 的图象上, 所以 5分 5分 所求点 的坐标为 的坐标为 6分 6分 (2)证明:由题意可设抛物线 的方程为 的方程为 即 由抛物线 过电 过电 ,于是又 ,于是又 由此可得 9分 9分 故 所以 , 11分 , 11分 于是   故  < < 14分 14分
| | | | | | | | | | | | | | | |

 为 ( )
为 ( ) 的解集是 ( )
的解集是 ( ) B.(0,1) C.(1,2) D.
B.(0,1) C.(1,2) D.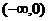
 关于原点对称,则圆C的方程为 ( )
关于原点对称,则圆C的方程为 ( ) B.
B.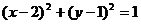
 D.
D.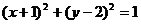
 的展开式的二项式系数之和为128,则n的值为 ( )
的展开式的二项式系数之和为128,则n的值为 ( ) 上单调递增的是 ( )
上单调递增的是 ( ) B.
B. C.
C. D.
D.
 的终边在 ( )
的终边在 ( ) 和两个平面
和两个平面 ,给出下列四个命题:
,给出下列四个命题: 内的任何直线都与
内的任何直线都与 平行;
平行; 内的任何直线都与
内的任何直线都与 垂直;
垂直; 内的任何直线都与
内的任何直线都与 平行;
平行; 内的任何直线都与
内的任何直线都与 垂直;
垂直;