练习册

  • 练习册
  • 试题
    (2)设函数在区间[-3.0]上的最大值和最小值. 【查看更多】

     

    题目列表(包括答案和解析)

    设函数设函数f（x）定义在（0，+∞）上，f（1）=0，导函数f′(x)=
    1
    x
    ，g（x）=f（x）+f'（x）．
    （1）求g（x）的单调区间和最小值；
    （2）讨论g（x）与g(
    1
    x
    )    的大小关系；
    （3）是否存在x0＞0，使得|g(x)-g(x0)|＜
    1
    x
    对任意x＞0成立？若存在，求出x0的取值范围；若不存在，请说明理由．

    查看答案和解析>>

    设函数f（x）=asinωx+bcosωx（ω＞0）的定义域为R，最小正周期为π，且对任意实数x，恒有f(x)≤f(
    π12
    )=4    成立．
    （1）求实数a和b的值；
    （2）作出函数f（x）在区间（0，π）上的大致图象；
    （3）若两相异实数x1、x2∈（0，π），且满足f（x1）=f（x2），求f（x1+x2）的值．

    查看答案和解析>>

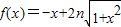    已知函数在区间（0，∞）上的最小值是an（n∈N*）．
    （1）求an；
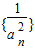    （2）设Sn为数列的前n项的和，求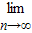Sn的值；
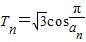
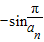    （3）若 ，试比较Tn与Tn+1的大小．

    查看答案和解析>>

    设函数f(x)定义在(0，＋∞)上，f(1)＝0，导函数，．

    (1)求g(x)的单调区间和最小值；

    (2)讨论g(x)与的大小关系；

    (3)是否存在x0＞0，使得对任意x＞0成立？若存在，求出x0的取值范围；若不存在，请说明理由．

    查看答案和解析>>

    设函数f（x）定义在（0，+∞）上，f（1）=0，导函数，.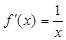
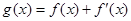    （1）求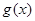的单调区间和最小值；
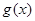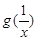    （2）讨论与的大小关系；
    （3）是否存在x0＞0，使得|g（x）﹣g（x0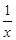）|＜对任意x＞0成立？若存在，求出x0的取值范围；若不存在请说明理由．

    查看答案和解析>>

     

    一、选择题（本大题共8小题，每小题5分，共40分）

    1―4DBAB  5―8CBAD

    二、填空题（本大题共6小题，每小题5分，有两空的小题，第一空3分，第二空2分，共30分）

    20090508

    10．                         

    11．36                 

    12．   

    13．56 

    14．

           注：两个空的填空题第一个空填对得3分，第二个空填对得2分。

    三、解答题（本大题共6小题，共80分）

    15．（本小题共13分）

           解：（1）依题意函数

           有

           故   4分

       （2）由

           原不等式等价于   6分

           当时，    8分

           当时，   10分

           当时，

           此时不等式组无解    12分

           所以，当时，不等式的解集为

           当时，不等式的解集为

           当时，不等式的解集为空集。     13分

    16．（本小题满分13分）

           解：（1）由得

              4分

          

              6分

           所以   8分

           又由

           得

           故单调递减区间是

              10

       （2）由

           故   12分

           又

           得    12分

           所以   13分

    17．（本小题满分14分）

           *为BD中点，E为PD中点，

               3分

           平面AEC，PB平面AEC，

           PB//平面AEC。   6分

       （2）解法一：取AD中点L，

    过L作于K，连结EK，EL，

           *L为AD中点，

           EL//PA，

           *LK为EK在平面ABCD内的射影。

           又

           为二面角E―AC―D的平面角     10分

           在

           ∽

          

           设正方形边长为2，

           则   12分

           在

           二面角E―AC―D的大小为   14分

     

     

     

     

           解法二：

       （2）如图，以A为坐标原点，AB，AD，AP所在直线分别为

           由，设正方形边长为2，

    则（0，0，0），（2，0，0），（2，2，0），

           （0，2，0），P（0，0，2），E（0，1，1）10分

           ∵⊥平面，

           ∴是平面的法向量，=（0，0，2），

           设面AEC的法向量为

          

           则

           令，则（1，-1，1）                                                                      12分

           =。

           ∴二面角的大小为arccos。                                                   14分

    18．（本小题满分13分）

         解：（1），                                                       2分

           根据题意有                                                                                4分

           解得                                                                             6分

       （2）由（1）知

           则                                                                       7分

                                                                                                8分

           令，即解得或                               11分

           令，即解得             

           当在[-3，0]内变化时，与的变化情况如下：

    -3

    （-3，-2）

    -2

    （-2，0）

    0

    +

    +

    0

    -

    -

    -10

    ㄊ

    极大值

    ㄋ

    -16

           当时，有最小值-16；当时，有最大值0                    13分

    19．（本小题满分13分）

         解：（1）恰用3发子弹就将油罐引爆记为事件A，则

           即恰用3发子弹将油罐引爆的概率为                                                         6分

       （2）记“油罐被引爆”的事件为事件B，其对立事件为

           则                                                           10分

           故

           即油罐被引爆的概率为                                                                            13分

    20．（本小题满分14分）

         解：（1）由的横坐标成以为首项，-1为公差的等差数列，

           故。                                             3分

           又位于函数的图象上，

           所以                                            5分

           所求点的坐标为                                                 6分

       （2）证明：由题意可设抛物线的方程为

           即

           由抛物线过电，于是又

           由此可得                                                       9分

           故

           所以，                       11分

           于是

          

          

           故＜                                        14分

     

     

     

     

     

     


    同步练习册答案