
2009年泰州市中考模拟考试数学试题
(考试时间:120分钟 总分:150 分)
命题人:陆祥雪(省泰中附中) 孙友权(泰州高港实验学校)
审题人:缪选民
注意事项:
1、本试卷共分两部分,第Ⅰ卷为选择题,第Ⅱ卷为非选择题。
2、所有试题的答案均填写在答题卡上,答案写在试卷上无效。
第Ⅰ卷选择题(共24分)
一、选择题(下列各题所给答案中,只有一个答案是正确的,每小题3分,共24分)
1、 的相反数是
( )
的相反数是
( )
A.2 B.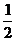 C.-2 D.
C.-2 D.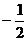
2、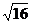 的计算结果是
( )
的计算结果是
( )
A.4 B.-
3、下列各式计算正确的是 ( )
A.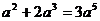 B.
B.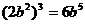
C.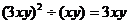 D.
D.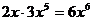
 4、二次函数
4、二次函数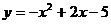 图象的顶点坐标为
( )
图象的顶点坐标为
( )
A.(-1,-4) B.(1,-4) C.(2,-1) D.(-2,-1)
5、已知∠a=65°,则∠a的余角等于
A. 15° B.25° C. 105° D.115°
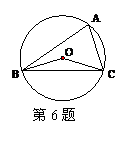
6、如图,⊙O是△ABC的外接圆,∠A=80°,则∠BOC等于 ( )
A.50° B.40° C.100° D.160°
7、下表是
城市
南京
徐州
连云港
淮安
盐城
宿迁
扬州
泰州
镇江
常州
无锡
苏州
南通
温度℃
11~4
9~2
9~1
10~3
10~3
10~1
12~5
13~3
11~6
12~3
14~6
16~4
13~4
A.10,4 B.10,
8、如图,在梯形ABCD中,AB∥CD,AB⊥BC,AB=1,BC=4,E为BC中点,AE平分∠BAD,连接DE,则sin∠ADE的值为 ( )
 A.
A.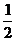 B.
B.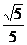 C.
C.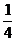 D.
D.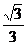
第Ⅱ卷非选择题(共126分)
二、填空题(每题3分,共30分)
9、函数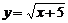 中自变量x的取值范围是 .
中自变量x的取值范围是 .
10、不等式组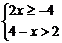 的解集是 .
的解集是 .
11、随着我国综合国力的增强,全球学习汉语的人数不断增加,据报道2008年海外学习汉语的人数已达43600000人,数据43600000用科学记数法表示为 .
12、已知一个圆锥的底面半径为4,母线长为8,则该圆锥的侧面积为 .
13、方程3x2-4x+1=0的一个根为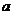 ,则
,则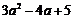 的值为 .
的值为 .
14、某书店把一本新书按标价的九折出售,仍可获利20%.若该书的进价为21元,则标价
为 元.
15、如图,l1∥l2,∠a= 度.
16、已知a+b=6,ab=3,则a2b+ab2= .
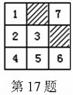
17、如图,在3×3的正方形网格中,已有两个小正方形被涂黑,再将图中的一个小正方形涂黑,所得图案是一个轴对称图形,则涂黑的小正方形可以是 (填出所有符合要求的小正方形的标号).
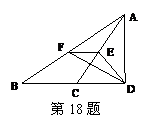
18、如图,在△ABD中,∠ADB=90°,C是BD上一点,若E、F分别是AC、AB的中点,△DEF的面积为3.5,则△ABC的面积为 .
 |
 |
三、解答题
19、计算或化简(本题满分8分)
(1) 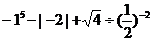 (2)
(2)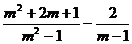
20、解方程组或不等式(本题满分8分)
(1)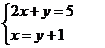 (2)
(2)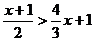
21、(本题满分8分)
去年3月12日某校学生参加植树活动,在引江河两岸共栽A、B、C三种不同品种的树苗1500棵.今年植树节前同学们去引江河两岸调查了A、B、C三种品种树苗的成活情况,准备今年从三种品种中选成活率最高的品种进行栽种。经调查,A品种的成活率为90%,C品种的成活率为92%,三种品种的总成活率为92.2%,并把成活的棵数绘制成如下不完整的统计图.
 (1)三种品种树苗去年各栽了多少棵?
(1)三种品种树苗去年各栽了多少棵?
(2)补全条形统计图,并通过计算说明今年应栽哪种品种的树苗.
22、(本题满分8分)
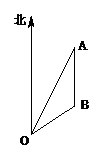 如图,在海岸边有一港口O,已知小岛A在港口O北偏东30°的方向上,小岛B在小岛A的正南方向,OA=60海里,OB=20海里.
如图,在海岸边有一港口O,已知小岛A在港口O北偏东30°的方向上,小岛B在小岛A的正南方向,OA=60海里,OB=20海里.
(1)求O到直线AB的距离;
(2)小岛B在港口O的什么方向上?
23、(本题满分10分)
一个不透明的口袋里装有红、白、黄三种颜色的乒乓球(除颜色外其余都相同),其中有白球2个,黄球1个,若从中任意摸出一个球,这个球是白球的概率为0.5.
(1)求口袋中红球的个数;
(2)若从中摸出一个球后不放回,再摸出一个球,通过画树状图或列表分析,求两次均摸到白球的概率.
24、(本题满分10分)
如图,在△ABE中,BA=BE,C在BE上,D在AB上,且AD=AC=BC.
(1)若∠B=40°,求∠BCD的大小;
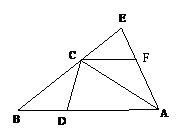 (2)过C作CF∥AB交AE于F, 求证:CF=BD.
(2)过C作CF∥AB交AE于F, 求证:CF=BD.
25、(本题满分10分)
我们在园林游玩时,常见到如图所示的圆弧形的门,若圆弧所在圆与地面BC相切于E点,四边形ABCD是一个矩形.已知AB= 米,BC=
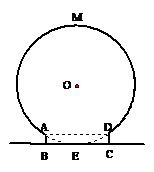 (1)求圆弧形门最高点到地面的距离;
(1)求圆弧形门最高点到地面的距离;
(2)求弧AMD的长.
26、(本题满分10分)
 如图,反比例函数
如图,反比例函数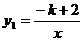 (x>0)与一次函数
(x>0)与一次函数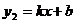 的图象相交于A、B两点,已知当y2>y1时,x的取值范围是1<x<3.
的图象相交于A、B两点,已知当y2>y1时,x的取值范围是1<x<3.
(1)求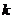 、
、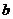 的值;
的值;
(2)求△AOB的面积.
27、(本题满分12分)
在矩形ABCD中,AB=14,BC=8,E在线段AB上,F在射线AD上,
(1)沿EF翻折,使A落在CD边上的G处 (如图1) ,若DG=4,
①求AF的长;
②求折痕EF的长.
(2)若沿EF翻折后,点A总在矩形ABCD的内部,试求AE长的范围.

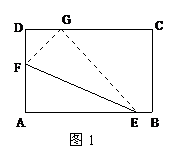 |
28、(本题满分12分)
如图,在平面直角坐标系中,已知四边形ABCD是等腰梯形,A、B在x轴上,D在y轴上,AB∥CD,AD=BC=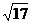 ,AB=5,CD=3,抛物线
,AB=5,CD=3,抛物线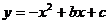 过A、B两点.
过A、B两点.
(1)求b、c;
(2)设M是x轴上方抛物线上的一动点,它到x轴与y轴的距离之和为d,求d的最大值;
(3)当(2)中M点运动到使d取最大值时,此时记点M为N,设线段AC与y轴交于点E,F为线段EC上一动点,求 F到N点与到y轴的距离之和的最小值,并求此时F点的坐标.

题号
1
2
3
4
5
6
7
8
答案
C
A
D
B
B
D
C
B
9、 10、
10、 11、
11、 12、32π 13、 4 14、28 15、35
12、32π 13、 4 14、28 15、35
16、18 17、2,3,4,5,7(多填少填均不得分) 18、14
19、(1)解 原式=-1-2+2÷4(2分) (2 解 原式= (2分)
(2分)
= (4分)
=
(4分)
=
=1 (4分)
20、(1)解:将(2)代入(1)得 (2) 解: 3(x+1)>8x+6 (2分)
2(y+1)+y=5 -5x>3
∴ y=1
(2分)
∴x< (4分)
(4分)
把y=1代入(2)得 x=2 ,
∴ (4分)
(4分)
21. (1)A品种树苗棵数
为540÷90%=600(棵)
C品种的树苗棵数为368÷92%=400(棵)
B品种树苗棵数为1500-600-400=500(棵)
答:去年A品种树苗栽600棵,B品种树苗栽500棵,C品种树苗栽400棵. (4分)
 (2)B品种成活棵数
(2)B品种成活棵数
为1500×92.2%-540-368=475(棵) (6分)
B品种成活率=
∴B品种成活率最高
∴今年应栽种B品种树苗. (8分)
22、解(1)OC=30 海里. (4分)
(2)在Rt△OBC中
 ∵OB=
∵OB= ,OC=30 ∴sin∠OBC=
,OC=30 ∴sin∠OBC=
∴∠OBC=60°
∴B在港口O的北偏东60°方向上 (8分)
23、(1)解:设红球的个数为x
 (2分)
(2分)
解得  (3分)
(3分)
经检验:x=1是所列方程根且符合题意 (4分)
所以口袋中红球的个数为1个 (5分)
(2)用树状图分析如下
 或列表分析:
或列表分析:
白球1
白球2
黄球
红球
白球1


(白2,白1)
(黄,白1)
(红,白1)
白球2
(白1,白2)
(黄,白2)
(红,白2)
黄球
(白1,黄)
(白2,黄)
(红,黄)
红球
(白1,红)
(白2,红)
(黄,红)
共有12种等可能结果 (8分)
其中2个白球的可能结果是2个.
 所以两次均摸到白球的概率为
所以两次均摸到白球的概率为 . (10分)
. (10分)
24、解(1)∵∠B=40°CB=CA∴∠CAB=40°又∵AC=AD∴∠ADC=70° (3分)
∴∠BCD=30° (5分)
(2)∵ BA=BE,∴∠BAE=∠BEA,
∵CF∥AB∴∠EFC=∠BAE ,
∴∠EFC=∠BEA ∴CE=CF , (7分)
 ∵BC=AC=AD, ∴CE=BD,
∵BC=AC=AD, ∴CE=BD,
∴CF=BD (10分)
25、解(1)设圆弧所在圆的圆心为O,
连接OE交AD于F,连接OA
设⊙O半径为x,则OF= 米, AF=
米, AF= 米
米
在Rt△AOF中
 (3分)
(3分)

圆弧门最高点到地面的距离为
(2)∵OA=1, OF=
 ∴∠AOF=60°∴∠AOD=120°(8分)
∴∠AOF=60°∴∠AOD=120°(8分)
弧AMD的长= 米
(10分)
米
(10分)
26、解(1)由已知得A、B的横坐标分别为1,3
 所以有
所以有 (3分)
(3分)
解得 (4分)
(4分)
(2)设直线AB交x轴于C点
由y2=-x+4 得
C(4,0),A(1,3),B(3,1) (8分)
∵S△AOC= ,S△BOC=
,S△BOC= ∴S△AOB=4 (10分)
∴S△AOB=4 (10分)
 27、(1)①设AF=x,则FG=x
27、(1)①设AF=x,则FG=x
在Rt△DFG中

解得 x=5, 所以AF=5 (4分)
② 过G作GH⊥AB于H, 设AE=y,
则HE=y-4. 在Rt△EHG中
 , 解得 y=10
, 解得 y=10
在Rt△AEF中,
EF= =
= (8分)
(8分)
方法二:连接AG,由△ADG∽△EAF得
 , 所以
, 所以 .∵AG=
.∵AG= , AH=
, AH= , FH=
, FH= ,
,
∴AF=5,∴AE=10∴EF= (8分)
(8分)
(2)假设A点翻折后的落点为P,则P应该在以E为圆心,EA长为半径的圆上。要保证P总在矩形内部,CD与圆相离,BC与圆也要相离,则满足关系式:
 ,
0<AE<7(仅写AE<7不扣分)
(12分)
,
0<AE<7(仅写AE<7不扣分)
(12分)
28、解(1)易得A(-1,0) B(4,0)
把x=-1,y=0;x=4,y=0分别代入

 得
得

解得 (3分)
(3分)
 (2)设M点坐标为
(2)设M点坐标为

①当 时,
时,


所以,当 时,d取最大值,值为4;
时,d取最大值,值为4;
②当0<a<4时,

所以,当 时,d取最大值,最大值为8;
时,d取最大值,最大值为8;
综合①、②得,d的最大值为8.
(不讨论a的取值情况得出正确结果的
得2分) (7分)
(3)N点的坐标为(2,6)
过A作y轴的平行线AH,过F作FG⊥y轴交AH于点Q,过F作FK⊥x轴于K,
∵∠CAB=45°, AC平分∠HAB,∴FQ=FK
∴FN+FG=FN+FK-1
所以,当N、F、K在一条直线上时,FN+FG=FN+FK-1最小,最小值为5.(10分)
易求直线AC的函数关系式为y=x+1,把x=2代入y=x+1得y=3,
所以F点的坐标为(2,3). (12分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com