练习册

  • 练习册
  • 试题
    精英家教网 > 试题搜索列表 >已知点P（n,2n

    已知点P（n,2n答案解析

    科目：czsx 来源： 题型：

    已知点P（n，2n）是第一象限的点，下面四个命题：
    ①点P关于y轴对称的点P1的坐标是（n，-2n）
    ②点P到原点O的距离是
    		5n

    ③直线y=-nx+2n不经过第三象限
    ④对于函数y=
    n
    x
    ，当x＜0时，y随x的增大而减小
    其中命题不正确的是
     
    （填上所有命题的序号如①②等）．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    已知抛物线y=x2+（2n-1）x+n2-1（n为常数）．
    （1）当该抛物线经过坐标原点，并且顶点在第四象限时，求出它所对应的函数关系式；
    （2）设A是（1）所确定的抛物线上位于x轴下方、且在对称轴左侧的一个动点，过A作x轴的平行线，交抛物线于另一点D，再作AB⊥x轴于B，DC⊥x轴于C．
    ①当BC=1时，求矩形ABCD的周长；
    ②试问矩形ABCD的周长是否存在最大值？如果存在，请求出这个最大值，并指出此时A点的坐标．如果不存在，请说明理由．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    23、已知点A（m-n，2-m）与点B（3n，-2n-m），如果点A、B关于原点对称，求m、n的值．

    查看答案和解析>>

    科目：czsx 来源： 题型：

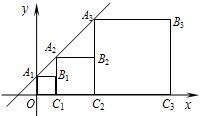    16、正方形A1B1C1O，A2B2C2C1，A3B3C3C2，…按如图所示的方式放置．点A1，A2，A3，…和点C1，C2，C3，…分别在直线y=kx+b（k＞0）和x轴上，已知点B1（1，1），B2（3，2），则Bn的坐标是
    （2n-1，2n-1）
    ．

    查看答案和解析>>

    科目：czsx 来源： 题型：

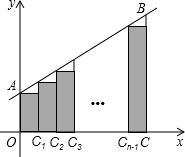    （2013•南平模拟）如图，在平面直角坐标系xOy中，直线y=x+b与y轴交于点A且经过点B（2，3），已知点C坐标为（2，0），点C1，C2，C3，…，Cn-1（n≥2）将线段OCn等分，图中阴影部分由n个矩形构成，记梯形AOCB面积为S，阴影部分面积为S′．
    下列四个结论中，正确的是
    ②③④
    ②③④
    ．（写出所有正确结论的序号）
    ①S=2﹔
    ②S′=4-
    2
    n
    ﹔
    ③随着n的增大，S′越来越接近S﹔
    ④若从梯形AOCB内任取一点，则该点取自阴影部分的概率是
    2n-1
    2n
    ．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    如图，已知点A（1，m），B（2，n）在反比例函数y=
    k1x
    的图象上，其中m，n是一元二次方程
    x2-2ax+a2-1=0的两根
    （1）写出m与n的数量关系
    m=2n
    m=2n
    ；并求出a的值；
    （2）设直线AB与x轴交于点C，AD⊥x轴于D点，E点与C点关于直线AD对称，连接EB交AD于P点，求AP的长度．

    查看答案和解析>>

    科目：czsx 来源： 题型：

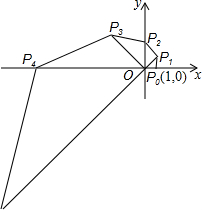    精英家教网如图，在直角坐标系中，已知点P0的坐标为（1，0），将线段OP0按逆时针方向旋转45°，再将其长度伸长为OP0的2倍，得到线段OP1；又将线段OP1按逆时针方向旋转45°，长度伸长为OP1的2倍，得到线段OP2；如此下去，得到线段OP3，OP4，…，OPn（n为正整数）．我们规定：把点Pn（xn，yn）（n=0，1，2，3，…）的横坐标xn、纵坐标yn都取绝对值后得到的新坐标（|xn|，|yn|）称之为点Pn的“绝对坐标”．则Pn的“绝对坐标”为（　　）
    A、（2n-1
    		2
    ，2n-1
    		2
    ）或（2n，0）
    B、（2n，0）或（0，2n）
    C、（0，2n）或（2n-1
    		2
    ，2n-1
    		2
    ）
    D、（2n-1
    		2
    ，2n-1
    		2
    ）或（2n，0）或（0，2n）

    查看答案和解析>>

    科目：czsx 来源： 题型：

    18、正方形A1B1C1O，A2B2C2C1，A3B3C3C2，…按如图所示的方式放置．点A1，A2，A3，…和点C1，C2，C3，…分别在直线y=kx+b（k＞0）和x轴上，已知点B1（1，1），B2（3，2），则Bn的坐标是
    （2n-1，2n-1）
    ．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    已知点A，B的坐标分别是（2m+n，2），（1，n-m）．若点A与点B关于y对称，则m+2n的值为（　　）

    查看答案和解析>>

    科目：czsx 来源： 题型：

    已知点P（2n-3，2n）在x轴上，则n的值是
    0
    0
    ．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    已知点A（m，n）在平面直角坐标系中的第三象限，其坐标m、n满足
    3m+2n=k-9
    2m+n=k-7
    ．
    （1）求整数解k的值；
    （2）当k为整数时，分解因式（a+b）3-k（a+b）．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    （2011•邯郸一模）正方形A1B1C1O，A2B2C2C1，A3B3C3C2，…按如图所示的方式放置．点A1，A2，A3，…和点C1，C2，C3，…分别在直线y=kx+b（k＞0）和x轴上，已知点B1（1，1），B2（3，2），则Bn的坐标是（　　）

    查看答案和解析>>

    科目：czsx 来源： 题型：

    14、已知点M（3n-2，2n+7）在第二，第四象限的角平分线上，则n=
    -1
    ．

    查看答案和解析>>

    科目：czsx 来源：第2章《二次函数》常考题集（26）：2.8 二次函数的应用（解析版） 题型：解答题

    已知抛物线y=x2+（2n-1）x+n2-1（n为常数）．
    （1）当该抛物线经过坐标原点，并且顶点在第四象限时，求出它所对应的函数关系式；
    （2）设A是（1）所确定的抛物线上位于x轴下方、且在对称轴左侧的一个动点，过A作x轴的平行线，交抛物线于另一点D，再作AB⊥x轴于B，DC⊥x轴于C．
    ①当BC=1时，求矩形ABCD的周长；
    ②试问矩形ABCD的周长是否存在最大值？如果存在，请求出这个最大值，并指出此时A点的坐标．如果不存在，请说明理由．

    查看答案和解析>>

    科目：czsx 来源：第23章《旋转》中考题集（04）：23.1 图形的旋转（解析版） 题型：解答题

    已知反比例函数y=的图象经过点A（-，1）．
    （1）试确定此反比例函数的解析式；
    （2）点O是坐标原点，将线段OA绕O点顺时针旋转30°得到线段OB．判断点B是否在此反比例函数的图象上，并说明理由；
    （3）已知点P（m，m+6）也在此反比例函数的图象上（其中m＜0），过P点作x轴的垂线，交x轴于点M．若线段PM上存在一点Q，使得△OQM的面积是，设Q点的纵坐标为n，求n2-2n+9的值．

    查看答案和解析>>

    科目：czsx 来源：第20章《二次函数和反比例函数》常考题集（25）：20.5 二次函数的一些应用（解析版） 题型：解答题

    已知抛物线y=x2+（2n-1）x+n2-1（n为常数）．
    （1）当该抛物线经过坐标原点，并且顶点在第四象限时，求出它所对应的函数关系式；
    （2）设A是（1）所确定的抛物线上位于x轴下方、且在对称轴左侧的一个动点，过A作x轴的平行线，交抛物线于另一点D，再作AB⊥x轴于B，DC⊥x轴于C．
    ①当BC=1时，求矩形ABCD的周长；
    ②试问矩形ABCD的周长是否存在最大值？如果存在，请求出这个最大值，并指出此时A点的坐标．如果不存在，请说明理由．

    查看答案和解析>>

    科目：czsx 来源：第2章《二次函数》常考题集（25）：2.4 二次函数的应用（解析版） 题型：解答题

    已知抛物线y=x2+（2n-1）x+n2-1（n为常数）．
    （1）当该抛物线经过坐标原点，并且顶点在第四象限时，求出它所对应的函数关系式；
    （2）设A是（1）所确定的抛物线上位于x轴下方、且在对称轴左侧的一个动点，过A作x轴的平行线，交抛物线于另一点D，再作AB⊥x轴于B，DC⊥x轴于C．
    ①当BC=1时，求矩形ABCD的周长；
    ②试问矩形ABCD的周长是否存在最大值？如果存在，请求出这个最大值，并指出此时A点的坐标．如果不存在，请说明理由．

    查看答案和解析>>

    科目：czsx 来源：第23章《二次函数与反比例函数》常考题集（24）：23.5 二次函数的应用（解析版） 题型：解答题

    已知抛物线y=x2+（2n-1）x+n2-1（n为常数）．
    （1）当该抛物线经过坐标原点，并且顶点在第四象限时，求出它所对应的函数关系式；
    （2）设A是（1）所确定的抛物线上位于x轴下方、且在对称轴左侧的一个动点，过A作x轴的平行线，交抛物线于另一点D，再作AB⊥x轴于B，DC⊥x轴于C．
    ①当BC=1时，求矩形ABCD的周长；
    ②试问矩形ABCD的周长是否存在最大值？如果存在，请求出这个最大值，并指出此时A点的坐标．如果不存在，请说明理由．

    查看答案和解析>>

    科目：czsx 来源：2011年河北省邯郸市中考数学一模试卷（解析版） 题型：选择题

    正方形A1B1C1O，A2B2C2C1，A3B3C3C2，…按如图所示的方式放置．点A1，A2，A3，…和点C1，C2，C3，…分别在直线y=kx+b（k＞0）和x轴上，已知点B1（1，1），B2（3，2），则Bn的坐标是（ ）

    A．（2n-1，2n-1）
    B．（2n-1+1，2n-1）
    C．（2n-1，2n-1）
    D．（2n-1，n）

    查看答案和解析>>

    科目：czsx 来源： 题型：

    已知反比例函数y=的图像经过点A(-，1)。

       (1) 试确定此反比例函数的解析式；

       (2) 点O是坐标原点，将线段OA绕O点顺时针旋转30°得到线段OB。判断点B是否在此

          反比例函数的图像上，并说明理由；

       (3) 已知点P(m，m+6)也在此反比例函数的图像上(其中m<0)，过P点作x轴的垂线，交

          x轴于点M。若线段PM上存在一点Q，使得△OQM的面积是，设Q点的纵坐标为n，

          求n2-2n+9的值。

    查看答案和解析>>