科目:czsx 来源: 题型:
科目:czsx 来源: 题型:

| 75 |
| 16 |
| 75 |
| 16 |
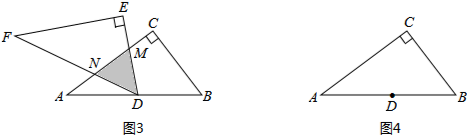
科目:czsx 来源: 题型:
数学活动——求重叠部分的面积。
问题情境:数学活动课上,老师出示了一个问题:
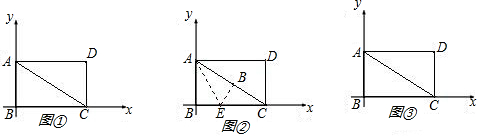
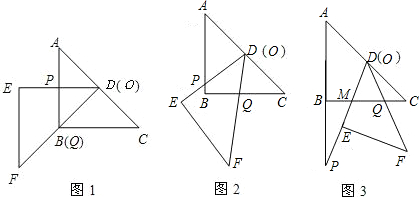
如图,将两块全等的直角三角形纸片△ABC和△DEF叠放在一起,其中∠ACB=∠E=90°,BC=DE=6,AC=FE=8,顶点D与边AB的中点重合,DE经过点C,DF交AC于点G。
求重叠部分(△DCG)的面积。
(1)独立思考:请解答老师提出的问题。
(2)合作交流:“希望”小组受此问题的启发,将△DEF绕点D旋转,使DE⊥AB交AC于点H,DF交AC于点G,如图(2),你能求出重叠部分(△DGH)的面积吗?请写出解答过程。
(3)提出问题:老师要求各小组向“希望”小组学习,将△DEF绕点D旋转,再提出一个求重叠部分面积的问题。“爱心”小组提出的问题是:如图(3),将△DEF绕点D旋转,DE,DF分别交AC于点M,N,使DM=MN求重叠部分(△DMN)的面积、
任务:①请解决“爱心”小组所提出的问题,直接写出△DMN的面积是
②请你仿照以上两个小组,大胆提出一个符合老师要求的问题,并在图中画出图形,标明字母,不必解答(注:也可在图(1)的基础上按顺时针方向旋转)。
科目:czsx 来源:2013年初中毕业升学考试(山西卷)数学(解析版) 题型:解答题
数学活动——求重叠部分的面积。
问题情境:数学活动课上,老师出示了一个问题:

如图(1),将两块全等的直角三角形纸片△ABC和△DEF叠放在一起,其中∠ACB=∠E=90°,BC=DE=6,AC=FE=8,顶点D与边AB的中点重合,DE经过点C,DF交AC于点G。
求重叠部分(△DCG)的面积。
(1)独立思考:请解答老师提出的问题。
(2)合作交流:“希望”小组受此问题的启发,将△DEF绕点D旋转,使DE⊥AB交AC于点H,DF交AC于点G,如图(2),你能求出重叠部分(△DGH)的面积吗?请写出解答过程。
(3)提出问题:老师要求各小组向“希望”小组学习,将△DEF绕点D旋转,再提出一个求重叠部分面积的问题。“爱心”小组提出的问题是:如图(3),将△DEF绕点D旋转,DE,DF分别交AC于点M,N,使DM=MN,求重叠部分(△DMN)的面积。
任务:①请解决“爱心”小组所提出的问题,直接写出△DMN的面积是 .
②请你仿照以上两个小组,大胆提出一个符合老师要求的问题,并在图中画出图形,标明字母,不必解答(注:也可在图(1)的基础上按顺时针方向旋转)。
科目:czsx 来源:2013年山西省高级中等学校招生考试数学 题型:044
数学活动——求重叠部分的面积.
问题情境:数学活动课上,老师出示了一个问题:
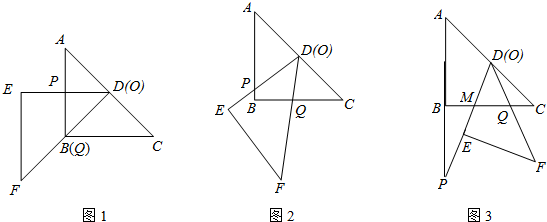
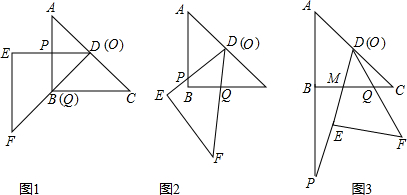
如图1,将两块全等的直角三角形纸片△ABC和△DEF叠放在一起,其中∠ACB=∠E=90°,BC=DE=6,AC=FE=8,顶点D与边AB的中点重合,DE经过点C,DF交AC于点G.求重叠部分(△DCG)的面积.
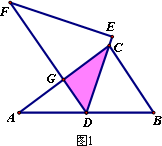
(1)独立思考:请解答老师提出的问题.
(2)合作交流:“希望”小组受此问题的启发,将△DEF绕点D旋转,使DE⊥AB交AC于点H,DF交AC于点G,如图2,你能求出重叠部分(△DGH)的面积吗?请写出解答过程.
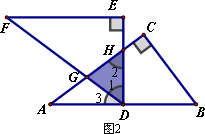
(3)提出问题:老师要求各小组向“希望”小组学习,将△DEF绕点D旋转,再提出一个求重叠部分面积的问题.“爱心”小组提出的问题是:如图3,将△DEF绕点D旋转,DE,DF分别交AC于点M,N,使DM=MN求重叠部分(△DMN)的面积、

任务:①请解决“爱心”小组所提出的问题,直接写出△DMN的面积是________.
②请你仿照以上两个小组,大胆提出一个符合老师要求的问题,并在图中画出图形,标明字母,不必解答(注:也可在图(1)的基础上按顺时针方向旋转).
科目:czsx 来源: 题型:解答题
科目:czsx 来源:2013年山西省中考数学试卷(解析版) 题型:解答题
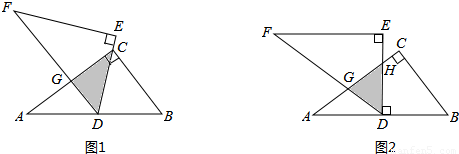
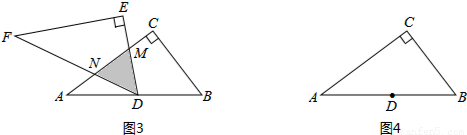
科目:czsx 来源:2013年山西省太原市中考数学试卷(解析版) 题型:解答题

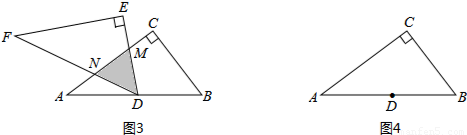
科目:czsx 来源: 题型:
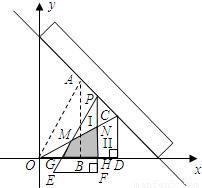
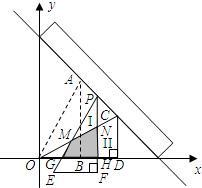 从上方紧靠两纸板放置,让纸板Ⅰ沿直尺边缘平行移动.当纸板Ⅰ移动至△PEF处时,设PE,PF与OC分别交于点M,N,与x轴分别交于点G,H.
从上方紧靠两纸板放置,让纸板Ⅰ沿直尺边缘平行移动.当纸板Ⅰ移动至△PEF处时,设PE,PF与OC分别交于点M,N,与x轴分别交于点G,H.科目:czsx 来源: 题型:
科目:czsx 来源: 题型:
科目:czsx 来源: 题型:
科目:czsx 来源: 题型:

科目:czsx 来源:2008年初中毕业升学考试(江苏连云港卷)数学(解析版) 题型:解答题
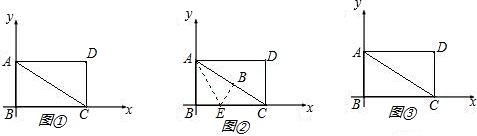
如图,现有两块全等的直角三角形纸板Ⅰ,Ⅱ,它们两直角边的长分别为1和2.将它们分别放置于平面直角坐标系中的 ,
, 处,直角边
处,直角边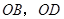 在
在 轴上.一直尺从上方紧靠两纸板放置,让纸板Ⅰ沿直尺边缘平行移动.当纸板Ⅰ移动至
轴上.一直尺从上方紧靠两纸板放置,让纸板Ⅰ沿直尺边缘平行移动.当纸板Ⅰ移动至 处时,设
处时,设 与
与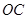 分别交于点
分别交于点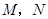 ,与
,与 轴分别交于点
轴分别交于点 .
.
(1)求直线 所对应的函数关系式;
所对应的函数关系式;
(2)当点 是线段
是线段 (端点除外)上的动点时,试探究:
(端点除外)上的动点时,试探究:
①点 到
到 轴的距离
轴的距离 与线段
与线段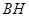 的长是否总相等?请说明理由;
的长是否总相等?请说明理由;
②两块纸板重叠部分(图中的阴影部分)的面积 是否存在最大值?若存在,求出这个最大值及
是否存在最大值?若存在,求出这个最大值及 取最大值时点
取最大值时点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

科目:czsx 来源:2008年初中毕业升学考试(江苏连云港卷)数学(带解析) 题型:解答题
如图,现有两块全等的直角三角形纸板Ⅰ,Ⅱ,它们两直角边的长分别为1和2.将它们分别放置于平面直角坐标系中的 ,
, 处,直角边
处,直角边 在
在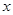 轴上.一直尺从上方紧靠两纸板放置,让纸板Ⅰ沿直尺边缘平行移动.当纸板Ⅰ移动至
轴上.一直尺从上方紧靠两纸板放置,让纸板Ⅰ沿直尺边缘平行移动.当纸板Ⅰ移动至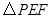 处时,设
处时,设 与
与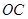 分别交于点
分别交于点 ,与
,与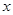 轴分别交于点
轴分别交于点 .
.
(1)求直线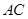 所对应的函数关系式;
所对应的函数关系式;
(2)当点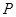 是线段
是线段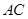 (端点除外)上的动点时,试探究:
(端点除外)上的动点时,试探究:
①点 到
到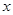 轴的距离
轴的距离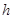 与线段
与线段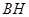 的长是否总相等?请说明理由;
的长是否总相等?请说明理由;
②两块纸板重叠部分(图中的阴影部分)的面积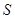 是否存在最大值?若存在,求出这个最大值及
是否存在最大值?若存在,求出这个最大值及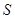 取最大值时点
取最大值时点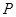 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.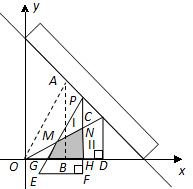
科目:czsx 来源:2009年北京市密云县中考数学二模试卷(解析版) 题型:解答题

科目:czsx 来源:第34章《二次函数》常考题集(23):34.4 二次函数的应用(解析版) 题型:解答题

科目:czsx 来源:第23章《二次函数与反比例函数》常考题集(22):23.5 二次函数的应用(解析版) 题型:解答题