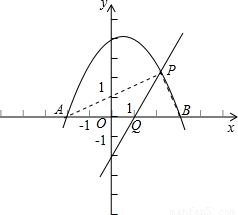精英家教网 >
试题搜索列表 >已知抛物线顶点为p(3,2)且与x轴交于A(1,0),求出抛物线所对应的二次函数的关系式
已知抛物线顶点为p(3,2)且与x轴交于A(1,0),求出抛物线所对应的二次函数的关系式答案解析
科目:czsx
来源:
题型:
在平面直角坐标系xOy中,已知抛物线y=-
(x-2)2+c与x轴交于A、B两点(点A在点B的左侧),交y轴的正半轴于点C,其顶点为M,MH⊥x轴于点H,MA交y轴于点N,sin∠MOH=
.
(1)求此抛物线的函数表达式;
(2)过H的直线与y轴相交于点P,过O,M两点作直线PH的垂线,垂足分别为E,F,若
=
时,求点P的坐标;
(3)将(1)中的抛物线沿y轴折叠,使点A落在点D处,连接MD,Q为(1)中的抛物线上的一动点,直线NQ交x轴于点G,当Q点在抛物线上运动时,是否存在点Q,使△ANG与△ADM相似?若存在,求出所有符合条件的
直线QG的解析式;若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
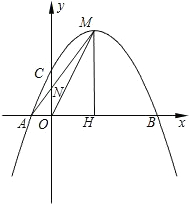
如图,已知抛物线
y=a(x-1)2-与x轴交于A,B两点(A在左边),抛物线经过点D(5,-3
),顶点为M.
(1)写出M点的坐标,并指出函数y有最大值还是最小值?这个值是多少?
(2)求a的值;
(3)以AB为直径画⊙P,试判定点D与⊙P的位置关系,并证明.
查看答案和解析>>
科目:czsx
来源:2011年初中毕业升学考试(江苏宿迁卷)数学
题型:解答题
查看答案和解析>>
科目:czsx
来源:
题型:
如图,已知抛物线
y=
x2+
bx+
c与
x轴交于
A、
B两点(
A点在
B点左侧),与y
轴交于点
C(0,-3),对称轴是直线
x=1,直线
BC与抛物线的对称轴交于点
D.
⑴求抛物线的函数表达式;
⑵求直线
BC的函数表达式;
⑶点
E为
y轴上一动点,
CE的垂直平分线交
CE于点
F,交抛物线于
P、
Q两点,且点
P在第三象限.
①当线段
PQ=
 AB
AB时,求
tan∠
CED的值;
②当以点
C、
D、
E为顶点的三角形是直角三角形时,请直接写出点
P的坐标.
温馨提示:考生可以根据第⑶问的题意,在图中补出图形,以便作答.

查看答案和解析>>
科目:czsx
来源:2012届江苏无锡滨湖中学九年级中考二模数学试卷(带解析)
题型:解答题
如图,已知抛物线y=x2+bx+c与x轴交于A、B两点(A点在B点左侧),
与y轴交于点C(0,-3),对称轴是直线x=1,直线BC与抛物线的对称轴交于点D.
【小题1】求抛物线的函数表达式
【小题2】求直线BC的函数表达式
【小题3】点E为y轴上一动点,CE的垂直平分线交CE于点F,交抛物线于P、Q两点,且点P在第三象限.
①当线段PQ= AB时,求tan∠CED的值;
AB时,求tan∠CED的值;
②当以点C、D、E为顶点的三角形是直角三角形时,请直接写出点P的坐标。
查看答案和解析>>
科目:czsx
来源:2011年中考数学模拟冲刺卷(4)(解析版)
题型:解答题
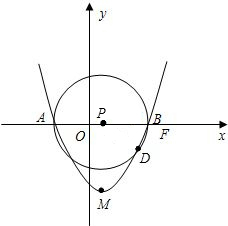
如图,点M(4,0),以点M为圆心、2为半径的圆与x轴交于点A、B,已知抛物线

过点A和B,与y轴交于点C.
(1)求点C的坐标,并画出抛物线的大致图象;
(2)求出抛物线的顶点D的坐标,并确定与圆M的位置关系;
(3)点Q(8,m)在抛物线

上,点P为此抛物线对称轴上一个动点,求PQ+PB的最小值.

查看答案和解析>>
科目:czsx
来源:
题型:解答题
如图,点M(4,0),以点M为圆心、2为半径的圆与x轴交于点A、B,已知抛物线 过点A和B,与y轴交于点C.
过点A和B,与y轴交于点C.
(1)求点C的坐标,并画出抛物线的大致图象;
(2)求出抛物线的顶点D的坐标,并确定与圆M的位置关系;
(3)点Q(8,m)在抛物线 上,点P为此抛物线对称轴上一个动点,求PQ+PB的最小值.
上,点P为此抛物线对称轴上一个动点,求PQ+PB的最小值.
查看答案和解析>>
科目:czsx
来源:2011-2012年北京房山区九年级第一学期期末考试数学卷
题型:解答题
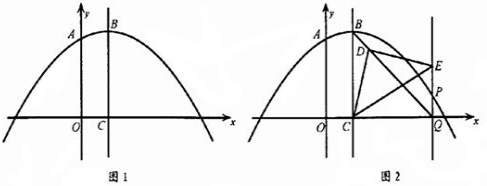
已知抛物线y=﹣ x2+bx+c的对称轴为直线x=1,最小值为3,此抛物线与y轴交于点A,顶点为B,对称轴BC与x轴交于点C.
x2+bx+c的对称轴为直线x=1,最小值为3,此抛物线与y轴交于点A,顶点为B,对称轴BC与x轴交于点C.
1.(1)求抛物线的解析式.
2.(2)如图1.求点A的坐标及线段OC的长;
3.(3)点P在抛物线上,直线PQ∥BC交x轴于点Q,连接BQ.
①若含45°角的直角三角板如图2所示放置.其中,一个顶点与点C重合,直角顶点D在BQ上,另一 个顶点E在PQ上.求直线BQ的函数解析式;
②若含30°角的直角三角板一个顶点与点C重合,直角顶点D在直线BQ上,另一个顶点E在PQ上,求点P的坐标.

查看答案和解析>>
科目:czsx
来源:
题型:
已知抛物线y=﹣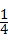 x2+bx+c的对称轴为直线x=1,最小值为3,此抛物线与y轴交于点A,顶点为B,对称轴BC与x轴交于点C.
x2+bx+c的对称轴为直线x=1,最小值为3,此抛物线与y轴交于点A,顶点为B,对称轴BC与x轴交于点C.
1.(1)求抛物线的解析式.
2.(2)如图1.求点A的坐标及线段OC的长;
3.(3)点P在抛物线上,直线PQ∥BC交x轴于点Q,连接BQ.
①若含45°角的直角三角板如图2所示放置.其中,一个顶点与点C重合,直角顶点D在BQ上,另一 个顶点E在PQ上.求直线BQ的函数解析式;
②若含30°角的直角三角板一个顶点与点C重合,直角顶点D在直线BQ上,另一个顶点E在PQ上,求点P的坐标.
查看答案和解析>>
科目:czsx
来源:2010年江苏省扬州市中考数学一模试卷(解析版)
题型:解答题
(2010•扬州一模)如图,点M(4,0),以点M为圆心、2为半径的圆与x轴交于点A、B,已知抛物线

过点A和B,与y轴交于点C.
(1)求点C的坐标,并画出抛物线的大致图象;
(2)求出抛物线的顶点D的坐标,并确定与圆M的位置关系;
(3)点Q(8,m)在抛物线

上,点P为此抛物线对称轴上一个动点,求PQ+PB的最小值.

查看答案和解析>>
科目:czsx
来源:2012年10月中考数学模拟试卷(12)(解析版)
题型:解答题
如图,点M(4,0),以点M为圆心、2为半径的圆与x轴交于点A、B,已知抛物线

过点A和B,与y轴交于点C.
(1)求点C的坐标,并画出抛物线的大致图象;
(2)求出抛物线的顶点D的坐标,并确定与圆M的位置关系;
(3)点Q(8,m)在抛物线

上,点P为此抛物线对称轴上一个动点,求PQ+PB的最小值.

查看答案和解析>>
科目:czsx
来源:
题型:
如图,已知抛物线y=x
2+bx+c与x轴交于A、B两点(A点在B点左侧),
与y轴交于点C(0,-3),对称轴是直线x=1,直线BC与抛物线的对称轴交于点D.
【小题1】求抛物线的函数表达式
【小题2】求直线BC的函数表达式
【小题3】点E为y轴上一动点,CE的垂直平分线交CE于点F,交抛物线于P、Q两点,且点P在第三象限.
①当线段PQ=
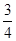
AB时,求tan∠CED的值;
②当以点C、D、E为顶点的三角形是直角三角形时,请直接写出点P的坐标。
查看答案和解析>>
科目:czsx
来源:1+1轻巧夺冠 同步讲解 九年级数学(下) 华东师大版
题型:044
|
|
已知抛物线y=ax2+bx+c满足下列条件,求函数的解析式
| (1) |
|
图象过两点A(1,0)、B(0,-3),且对称轴为直线x=2
|
|
(2) |
|
(3) |
|
图象与x轴交于(-2,0)、(4 ,0),且顶点为(1,-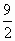 ) )
|
|
(4) |
|
图象顶点为(1,16)且与x轴交于两点,已知两交点距离为8个单位长度.
|
|
|
查看答案和解析>>
科目:czsx
来源:江苏省扬州市2010届九年级第一次模拟考试数学试题
题型:044
如图,点M(4,0),以点M为圆心、2为半径的圆与x轴交于点A、B.已知抛物线 过点A和B,与y轴交于点C.
过点A和B,与y轴交于点C.

(1)求点C的坐标,并画出抛物线的大致图象.
(2)求出抛物线的顶点D的坐标,并确定与圆M的位置关系.
(3)点Q(8,m)在抛物线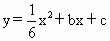 上,点P为此抛物线对称轴上一个动点,求PQ+PB的最小值.
上,点P为此抛物线对称轴上一个动点,求PQ+PB的最小值.
查看答案和解析>>
科目:czsx
来源:月考题
题型:解答题
已知抛物线y=ax2+bx+c(a≠0)与x轴交于原点O及点C,且与直线y=kx+4交于点A(1,m)和B(4,8).
(1)求直线和抛物线的解析式;
(2)设抛物线的顶点为D,连接DA、DB,求S△DAB?
查看答案和解析>>
科目:czsx
来源:
题型:
在平面直角坐标系中,已知A(-2,0)、B(4,0)两点,若抛物线经过A、B两点,且与y轴交于点(0,-2),求此抛物线的顶点坐标.
查看答案和解析>>
科目:czsx
来源:
题型:
如图,已知抛物线
c1:y=-x2+bx+c与x轴交于点A、B(点A在B的左侧),与y轴交于点C,抛物线c
2与抛物线c
1关于y轴对称,点A、B的对称点分别是E、D,连接CD、CB,设AD=m.
(1)抛物线c
2可以看成抛物线c
1向右平移
m
m
个单位得到.
(2)若m=2,求b的值.
(3)将△CDB沿直线BC折叠,点D的对应点为G,且四边形CDBG是平行四边形,
①△CDB为
等边
等边
三角形(按边分);
②若点G恰好落在抛物线c
2上,求m的值.
查看答案和解析>>
科目:czsx
来源:
题型:
如图,已知抛物线C:y=-
x
2+
x+3与x轴交于点A、B两点,过定点的直线l:y=
x-2(a≠0)交x轴于点Q.
(1)求证:不论a取何实数(a≠0)抛物线C与直线l总有两个交点;
(2)写出点A、B的坐标:A(
)、B(
)及点Q的坐标:Q(
)(用含a的代数式表示);并依点Q坐标的变化确定:当
时(填上a的取值范围),直线l与抛物线C在第一象限内有交点;
(3)设直线l与抛物线C在第一象限内的交点为P,是否存在这样的点P,使得
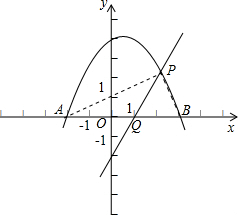
∠APB=90°?若存在,求出此时a的值;不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:专项题
题型:解答题
如图,已知抛物线y=ax2+ bx +3(a≠0)与x轴交于点A(1,0)和点B( -3,0),与y轴交于点C.
(1)求抛物线的解析式;
(2)设抛物线的对称轴与x轴交于点M,问在对称轴上是否存在点P,使△CMP为等腰三角形?若存在,请直接写出所有符合条件的点P坐标;若不存在,请说明理由.
(3)若点E为第二象限抛物线上一动点,连接BE、CE,求四边形BOCE面积的最大值,并求此时E点的坐标.
查看答案和解析>>
科目:czsx
来源:2004年全国中考数学试题汇编《二次函数》(05)(解析版)
题型:解答题
(2004•龙岩)如图,已知抛物线C:y=-

x
2+

x+3与x轴交于点A、B两点,过定点的直线l:y=
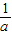
x-2(a≠0)交x轴于点Q.
(1)求证:不论a取何实数(a≠0)抛物线C与直线l总有两个交点;
(2)写出点A、B的坐标:A(______)、B(______)及点Q的坐标:Q(______)(用含a的代数式表示);并依点Q坐标的变化确定:当______时(填上a的取值范围),直线l与抛物线C在第一象限内有交点;
(3)设直线l与抛物线C在第一象限内的交点为P,是否存在这样的点P,使得∠APB=90°?若存在,求出此时a的值;不存在,请说明理由.
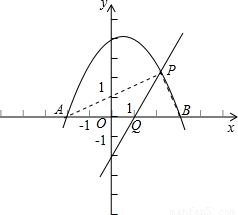
查看答案和解析>>

 直线QG的解析式;若不存在,请说明理由.
直线QG的解析式;若不存在,请说明理由.  ),顶点为M.
),顶点为M. 如图,已知抛物线y=x2+bx+c与x轴交于A、B两点(A点在B点左侧),与y
如图,已知抛物线y=x2+bx+c与x轴交于A、B两点(A点在B点左侧),与y AB时
AB时 ,求tan∠CED的值;
,求tan∠CED的值;
 AB时,求tan∠CED的值;
AB时,求tan∠CED的值;
 AB时,求tan∠CED的值;
AB时,求tan∠CED的值; 过点A和B,与y轴交于点C.
过点A和B,与y轴交于点C. 上,点P为此抛物线对称轴上一个动点,求PQ+PB的最小值.
上,点P为此抛物线对称轴上一个动点,求PQ+PB的最小值.
 过点A和B,与y轴交于点C.
过点A和B,与y轴交于点C. 上,点P为此抛物线对称轴上一个动点,求PQ+PB的最小值.
上,点P为此抛物线对称轴上一个动点,求PQ+PB的最小值.
 x2+bx+c的对称轴为直线x=1,最小值为3,此抛物线与y轴交于点A,顶点为B,对称轴BC与x轴交于点C.
x2+bx+c的对称轴为直线x=1,最小值为3,此抛物线与y轴交于点A,顶点为B,对称轴BC与x轴交于点C.
![]() x2+bx+c的对称轴为直线x=1,最小值为3,此抛物线与y轴交于点A,顶点为B,对称轴BC与x轴交于点C.
x2+bx+c的对称轴为直线x=1,最小值为3,此抛物线与y轴交于点A,顶点为B,对称轴BC与x轴交于点C.
 过点A和B,与y轴交于点C.
过点A和B,与y轴交于点C. 上,点P为此抛物线对称轴上一个动点,求PQ+PB的最小值.
上,点P为此抛物线对称轴上一个动点,求PQ+PB的最小值.
 过点A和B,与y轴交于点C.
过点A和B,与y轴交于点C. 上,点P为此抛物线对称轴上一个动点,求PQ+PB的最小值.
上,点P为此抛物线对称轴上一个动点,求PQ+PB的最小值.
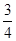 AB时,求tan∠CED的值;
AB时,求tan∠CED的值;![]() 过点A和B,与y轴交于点C.
过点A和B,与y轴交于点C.
![]() 上,点P为此抛物线对称轴上一个动点,求PQ+PB的最小值.
上,点P为此抛物线对称轴上一个动点,求PQ+PB的最小值.
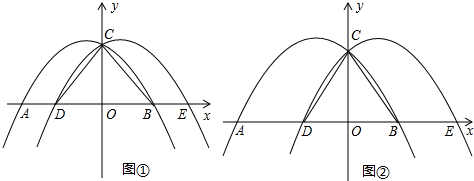
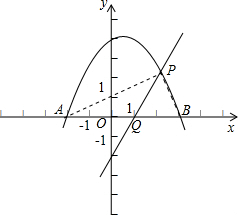 ∠APB=90°?若存在,求出此时a的值;不存在,请说明理由.
∠APB=90°?若存在,求出此时a的值;不存在,请说明理由. 
 x2+
x2+ x+3与x轴交于点A、B两点,过定点的直线l:y=
x+3与x轴交于点A、B两点,过定点的直线l:y=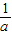 x-2(a≠0)交x轴于点Q.
x-2(a≠0)交x轴于点Q.