科目:czsx 来源: 题型:
科目:czsx 来源: 题型:解答题
科目:czsx 来源: 题型:
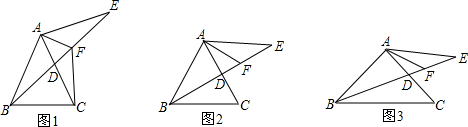
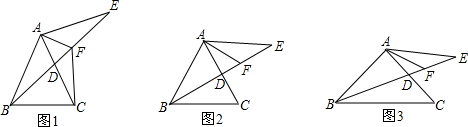
 如图,Rt△ABC中,AB=AC,点D为BC中点.∠MDN=90°,∠MDN绕点D旋转,DM、DN分别与边AB、AC交于E、F两点.下列结论:
如图,Rt△ABC中,AB=AC,点D为BC中点.∠MDN=90°,∠MDN绕点D旋转,DM、DN分别与边AB、AC交于E、F两点.下列结论:| 1 | 4 |
科目:czsx 来源: 题型:阅读理解

科目:czsx 来源: 题型:
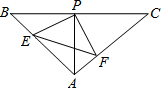 B、AC于点E、F,给出以下四个结论:
B、AC于点E、F,给出以下四个结论:| 1 | 2 |
科目:czsx 来源: 题型:
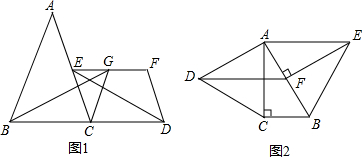
 (2013•莆田)定义:如图1,点C在线段AB上,若满足AC2=BC•AB,则称点C为线段AB的黄金分割点.
(2013•莆田)定义:如图1,点C在线段AB上,若满足AC2=BC•AB,则称点C为线段AB的黄金分割点.科目:czsx 来源: 题型:
科目:czsx 来源: 题型:
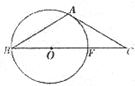 23、如图,等腰△ABC中,AB=AC.以AB为弦的⊙O交BC于F,且O在BC上.你认为∠C等于多少度时,
23、如图,等腰△ABC中,AB=AC.以AB为弦的⊙O交BC于F,且O在BC上.你认为∠C等于多少度时,科目:czsx 来源: 题型:
科目:czsx 来源: 题型:
 下列说法:
下列说法:科目:czsx 来源: 题型:
 在如图的等腰△ABC中,AB=AC.如果∠ABD=
在如图的等腰△ABC中,AB=AC.如果∠ABD=| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 4 |
科目:czsx 来源: 题型:
| 3 |
| 3 |
 大值,请回答:该最大值能否持续一个时段?若能,直接写出t的取值范围;若不能,请说明理由.
大值,请回答:该最大值能否持续一个时段?若能,直接写出t的取值范围;若不能,请说明理由. 科目:czsx 来源: 题型:
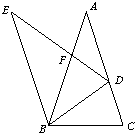 26、如图,等腰△ABC中,AB=AC,∠A=36°,△ABC 绕点B逆时针方向旋转一定角度后到△BDE的位置,点D落在边AC上,
26、如图,等腰△ABC中,AB=AC,∠A=36°,△ABC 绕点B逆时针方向旋转一定角度后到△BDE的位置,点D落在边AC上,科目:czsx 来源: 题型:
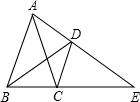 (2012•随州模拟)如图,等腰△ABC中,AB=AC,∠BAC=36°,以C为旋转中心,顺时针旋转△ABC到△DCE位置,使点A落在BC边的延长线上的E处,连接AD和BD.
(2012•随州模拟)如图,等腰△ABC中,AB=AC,∠BAC=36°,以C为旋转中心,顺时针旋转△ABC到△DCE位置,使点A落在BC边的延长线上的E处,连接AD和BD.科目:czsx 来源: 题型:
科目:czsx 来源: 题型:
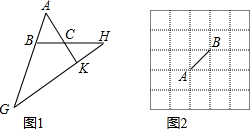
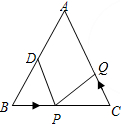 如图已知△ABC中,AB=AC=10厘米,∠B=∠C,BC=6厘米,点D为AB的中点.如果点P在线段BC上以1厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.若点Q的运动速度与点P的运动速度相等,经过
如图已知△ABC中,AB=AC=10厘米,∠B=∠C,BC=6厘米,点D为AB的中点.如果点P在线段BC上以1厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.若点Q的运动速度与点P的运动速度相等,经过科目:czsx 来源: 题型:
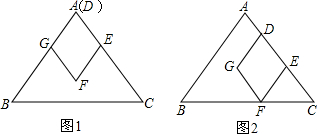
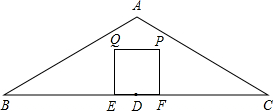
(9分)如图1,△ABC中,AB=AC=5cm,BC=6cm,边长为2cm的菱形DEFG两边DG、DE分别在AC、AB上.若菱形DEFG以1cm/s的速度沿射线AC方向平移.
(1)经过 ▲ 秒菱形DEFG的顶点F恰好在BC上;
(2)求菱形DEFG的面积;
(3)设菱形DEFG与△ABC的重合部分为Scm2,菱形DEFG平移的时间为t秒.求S与t的函数关系式.
科目:czsx 来源:2013年初中毕业升学考试(福建莆田卷)数学(解析版) 题型:解答题
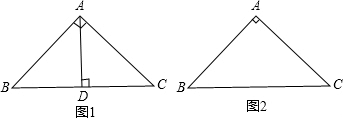
定义:如图1,点C在线段AB上,若满足AC2=BC•AB,则称点C为线段AB的黄金分割点.
如图2,△ABC中,AB=AC=1,∠A=36°,BD平分∠ABC交AC于点D.
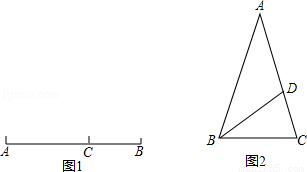
(1)求证:点D是线段AC的黄金分割点;
(2)求出线段AD的长.
科目:czsx 来源:2011-2012学年江苏盐城亭湖区九年级下学期第一次调研考试数学试卷(解析版) 题型:解答题
如图8,△ABC中,AB=AC,若点D在AB上,点E在AC上,请你加上一个条件,使结论BE=CD成立,同时补全图形,并证明此结论