
科目:gzsx 来源: 题型:
科目:gzsx 来源: 题型:
科目:gzsx 来源: 题型:
| Sn |
| n |
| 1 |
| 2 |
| 4 |
| 15 |
| MN |
| AB |
科目:gzsx 来源: 题型:
在(1+x)5+(1+x)6+(1+x)7的展开式中,含x4项的系数是首项为-2,公差为3的等差数列的( )
A.第11项 B.第13项
C.第18项 D.第20项
科目:gzsx 来源:2012-2013学年江西南昌八一、洪都、麻丘中学高三上期期中理科数学试卷(解析版) 题型:解答题
将数列 的各项按照第1行排
的各项按照第1行排 ,第2行自左至右排
,第2行自左至右排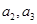 ,第3行…的规律,排成如图所示的三角形形状.
,第3行…的规律,排成如图所示的三角形形状.

(Ⅰ)若数列 是首项为1,公差为3的等差数列,写出图中第五行第五个数;
是首项为1,公差为3的等差数列,写出图中第五行第五个数;
(Ⅱ)若函数 且
且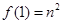 ,求数列
,求数列 的通项公式;
的通项公式;
(Ⅲ)设 为图中第
为图中第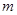 行所有项的和,在(Ⅱ)的条件下,用含
行所有项的和,在(Ⅱ)的条件下,用含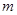 的代数式表示
的代数式表示 .
.
科目:gzsx 来源: 题型:
(14分)如果有穷数列a1,a2,…am(m为正整数)满足条件a1= am,a2= am-1,…,
am=a1,即ai=am-i+1(i=1,2, …,m),我们称其为“对称数列”.
(1)设{bn}是7项的“对称数列”,其中b1,b2,b3,b4是等差数列,且b1=2, b4=11,依次写出{bn}的每一项;
(2)设{Cn}是49项的“对称数列”,其中C25,C26,…,C49是首项为1,公比为2 的等比数列,求{Cn}各项的和S;
(3)设{dn}是100项的“对称数列”,其中d51,d52, …,d100是首项为2,公差为3的等差数列,求{dn}前n项的和Sn(n=1,2, …,100).科目:gzsx 来源:2010-2011年内蒙古高一第二学期期中考试(音体美类)数学 题型:选择题
数列 中,如果
中,如果 =3n(n=1,2,3,…) ,那么这个数列是 ( )
=3n(n=1,2,3,…) ,那么这个数列是 ( )
A.公差为2的等差数列 B.公差为3的等差数列
C.首项为3的等比数列 D.首项为1的等比数列
科目:gzsx 来源:2010年广东省高二下学期期末考试理科数学卷 题型:选择题
在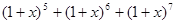 的展开式中,含
的展开式中,含 项的系数是首项为
项的系数是首项为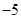 ,公差为3的等差数列的( )
,公差为3的等差数列的( )
A.第18项 B.第19项 C.第20项 D. 第21项
科目:gzsx 来源:2011-2012学年陕西省高三第一学期期末考试理科数学 题型:选择题
在 的展开式中,含
的展开式中,含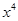 项的系数是首项为-2,公差为3的等差数列的( )
项的系数是首项为-2,公差为3的等差数列的( )
A.第11项 B.第13项 C.第18项 D.第20项
科目:gzsx 来源:2014届江苏省高二上期末文理数学试卷(选修)(解析版) 题型:解答题
(本题满分16分)
已知数列 ,其中
,其中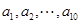 是首项为1,公差为1的等差数列;
是首项为1,公差为1的等差数列;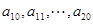 是公差为
是公差为 的等差数列;
的等差数列;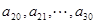 是公差为
是公差为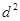 的等差数列(
的等差数列(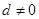 ).
).
(Ⅰ)若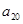 = 30,求
= 30,求 ;
;
(Ⅱ)试写出a30关于 的关系式,并求a30的取值范围;
的关系式,并求a30的取值范围;
(Ⅲ)续写已知数列,可以使得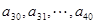 是公差为
是公差为 3的等差数列,请你依次类推,把已知数列推广为无穷数列,试写出
3的等差数列,请你依次类推,把已知数列推广为无穷数列,试写出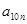 关于
关于 的关系式(
的关系式(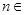 N
N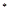 );
);
(Ⅳ)在(Ⅲ)条件下,且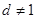 ,试用
,试用 表示此数列的前100项和
表示此数列的前100项和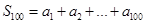
科目:gzsx 来源:2012-2013学年广东省茂名市高州三中高二(上)期中数学试卷(解析版) 题型:选择题
科目:gzsx 来源: 题型:
(1)设{bn}是项数为7的“对称数列”,其中b1,b2,b3,b4是等差数列,且b1=2,b4=11.依次写出{bn}的每一项.
(2)设{cn}是项数为2k-1(正整数k>1)的“对称数列”,其中ck,ck+1,…,c2k-1是首项为50,公差为-4的等差数列.记{cn}各项的和为S2k-1,当k为何值时,S2k-1取得最大值?并求出S2k-1的最大值.
(3)对于确定的正整数m>1,写出所有项数不超过2m的“对称数列”,使得1,2,22,…,2m-1依次是该数列中连续的项;当m>1 500时,求其中一个“对称数列”前2 008项的和S2008.
(文)如果有穷数列a1,a2,a3,…,am(m为正整数)满足条件a1=am,a2=am-1,…,am=a1,即ai=am-i+1(i=1,2,…,m),我们称其为“对称数列”.例如,数列1,2,5,2,1与数列8,4,2,2,4,8都是“对称数列”.
(1)设{bn}是7项的“对称数列”,其中b1,b2,b3,b4是等差数列,且b1=2,b4=11.依次写出{bn}的每一项;
(2)设{cn}是49项的“对称数列”,其中c25,c26,…,c49是首项为1,公比为2的等比数列,求{cn}各项的和S;
(3)设{dn}是100项的“对称数列”,其中d51,d52,…,d100是首项为2,公差为3的等差数列,求{dn}前n项的和Sn(n=1,2,…,100).
科目:gzsx 来源:101网校同步练习 高三数学 苏教版(新课标·2004年初审) 苏教版 题型:013
数列{an}是首项为2,公差为3的等差数列,数列{bn}是首项为-2,公差为4的等差数列![]() 若an=bn,则n的值为
若an=bn,则n的值为
A.4
B.5
C.6
D.7