数列an中，前N项和sn=2n2-13n+3,则sn的最小值答案解析
科目：gzsx
来源：
题型：
数列{a
n}中，前n项和
Sn=-n2-3，n∈N
*，则{a
n}的通项公式为a
n=
．
查看答案和解析>>
科目：gzsx
来源：
题型：
（2007•长宁区一模）数列{a
n}中，前n项和S
n=2
n（n为正整数），则a
n=
．
查看答案和解析>>
科目：gzsx
来源：
题型：
（2006•朝阳区一模）在各项均为正数的数列{an}中，前n项和Sn满足2Sn+1=an（2an+1），n∈N*．
（Ⅰ）证明{an}是等差数列，并求这个数列的通项公式及前n项和的公式；
（Ⅱ）在XOY平面上，设点列Mn（xn，yn）满足an=nxn，Sn=n2yn，且点列Mn在直线C上，Mn中最高点为Mk，若称直线C与x轴、直线x=a、x=b所围成的图形的面积为直线C在区间[a，b]上的面积，试求直线C在区间[x3，xk]上的面积；
（Ⅲ）是否存在圆心在直线C上的圆，使得点列Mn中任何一个点都在该圆内部？若存在，求出符合题目条件的半径最小的圆；若不存在，请说明理由．
查看答案和解析>>
科目：gzsx
来源：
题型：
数列{an}中，前n项和Sn=2n-1，求证：{an}是等比数列．
查看答案和解析>>
科目：gzsx
来源：
题型：
（2006•朝阳区一模）在各项均为正数的数列{an}中，前n项和Sn满足2Sn+1=an（2an+1），n∈N*．
（Ⅰ）证明{an}是等差数列，并求这个数列的通项公式及前n项和的公式；
（Ⅱ）在XOY平面上，设点列Mn（xn，yn）满足an=nxn，Sn=n2yn，且点列Mn在直线C上，Mn中最高点为Mk，若称直线C与x轴、直线x=a，x=b所围成的图形的面积为直线C在区间[a，b]上的面积，试求直线C在区间[x3，xk]上的面积．
查看答案和解析>>
科目：gzsx
来源：
题型：
在各项均为正数的数列{an}中，前n项和Sn满足2Sn+1=an（2an+1），n∈N*．
（1）证明{an}是等差数列，并求这个数列的通项公式及前n项和的公式；
（2）在平面直角坐标系xoy面上，设点Mn（xn，yn）满足an=nxn，Sn=n2yn，且点Mn在直线l上，Mn中最高点为Mk，若称直线l与x轴．直线x=a，x=b所围成的图形的面积为直线l在区间[a，b]上的面积，试求直线l在区间[x3，xk]上的面积；
（3）若存在圆心在直线l上的圆纸片能覆盖住点列Mn中任何一个点，求该圆纸片最小面积．
查看答案和解析>>
科目：gzsx
来源：
题型：
各项均为正数的数列{a
n}中，前n项和
Sn=()2．
（1）求数列{a
n}的通项公式；
（2）若
++…+＜k恒成立，求k的取值范围．
查看答案和解析>>
科目：gzsx
来源：
题型：
各项均为正数的数列{a
n}中，前n项和
Sn=()2．
（1）求数列{a
n}的通项公式；
（2）若
++…+＜k恒成立，求k的取值范围；
（3）对任意m∈N
*，将数列{a
n}中落入区间（2
m，2
2m）内的项的个数记为b
m，求数列{b
m}的前m项和S
m．
查看答案和解析>>
科目：gzsx
来源：
题型：
数列{an}中，前n项和Sn=3n+1，
（1）求a1；
（2）求通项公式an；
（3）该数列是等比数列吗？如不是，请说明理由；如是，请给出证明，并求出该等比数列的公比．
查看答案和解析>>
科目：gzsx
来源：2010年陕西省西安市阎良区高三数学测试卷（理科）（解析版）
题型：解答题
在各项均为正数的数列{an}中，前n项和Sn满足2Sn+1=an（2an+1），n∈N*．
（1）证明{an}是等差数列，并求这个数列的通项公式及前n项和的公式；
（2）在平面直角坐标系xoy面上，设点Mn（xn，yn）满足an=nxn，Sn=n2yn，且点Mn在直线l上，Mn中最高点为Mk，若称直线l与x轴．直线x=a，x=b所围成的图形的面积为直线l在区间[a，b]上的面积，试求直线l在区间[x3，xk]上的面积；
（3）若存在圆心在直线l上的圆纸片能覆盖住点列Mn中任何一个点，求该圆纸片最小面积．
查看答案和解析>>
科目：gzsx
来源：2009-2010学年上海市黄浦区大同中学高三（下）开学摸底数学试卷（理科）（解析版）
题型：解答题
在各项均为正数的数列{an}中，前n项和Sn满足2Sn+1=an（2an+1），n∈N*．
（1）证明{an}是等差数列，并求这个数列的通项公式及前n项和的公式；
（2）在平面直角坐标系xoy面上，设点Mn（xn，yn）满足an=nxn，Sn=n2yn，且点Mn在直线l上，Mn中最高点为Mk，若称直线l与x轴．直线x=a，x=b所围成的图形的面积为直线l在区间[a，b]上的面积，试求直线l在区间[x3，xk]上的面积；
（3）若存在圆心在直线l上的圆纸片能覆盖住点列Mn中任何一个点，求该圆纸片最小面积．
查看答案和解析>>
科目：gzsx
来源：2010年高三备考数学好题系列（11）（解析版）
题型：解答题
在各项均为正数的数列{an}中，前n项和Sn满足2Sn+1=an（2an+1），n∈N*．
（1）证明{an}是等差数列，并求这个数列的通项公式及前n项和的公式；
（2）在平面直角坐标系xoy面上，设点Mn（xn，yn）满足an=nxn，Sn=n2yn，且点Mn在直线l上，Mn中最高点为Mk，若称直线l与x轴．直线x=a，x=b所围成的图形的面积为直线l在区间[a，b]上的面积，试求直线l在区间[x3，xk]上的面积；
（3）若存在圆心在直线l上的圆纸片能覆盖住点列Mn中任何一个点，求该圆纸片最小面积．
查看答案和解析>>
科目：gzsx
来源：2010年陕西省西安市西工大附中高考数学三模试卷（理科）（解析版）
题型：解答题
在各项均为正数的数列{an}中，前n项和Sn满足2Sn+1=an（2an+1），n∈N*．
（1）证明{an}是等差数列，并求这个数列的通项公式及前n项和的公式；
（2）在平面直角坐标系xoy面上，设点Mn（xn，yn）满足an=nxn，Sn=n2yn，且点Mn在直线l上，Mn中最高点为Mk，若称直线l与x轴．直线x=a，x=b所围成的图形的面积为直线l在区间[a，b]上的面积，试求直线l在区间[x3，xk]上的面积；
（3）若存在圆心在直线l上的圆纸片能覆盖住点列Mn中任何一个点，求该圆纸片最小面积．
查看答案和解析>>
科目：gzsx
来源：2008年高考冲刺解答题突破、数学
题型：044
在各项均为正数的数列{an}中，前n项和Sn满足2Sn＋1＝an(2an＋1)，n∈N*．
(I)证明{an}是等差数列，并求这个数列的通项公式及前n项和的公式；
(II)在XOY平面上，设点列Mn(xn，yn)满足an＝nxn，Sn＝n2yn，且点列Mn在直线C上，Mn中最高点为Mk，若称直线C与x轴、直线x＝a、x＝b所围成的图形的面积为直线C在区间[a，b]上的面积，试求直线C在区间[x3，xk]上的面积；
(III)是否存在圆心在直线C上的圆，使得点列Mn中任何一个点都在该圆内部？若存在，求出符合题目条件的半径最小的圆；若不存在，请说明理由．
查看答案和解析>>
科目：gzsx
来源：
题型：填空题
数列{an}中，前n项和Sn=2n（n为正整数），则an=________．
查看答案和解析>>
科目：gzsx
来源：
题型：044
已知在正整数数列{an}中，前n项和Sn满足：Sn＝
(an＋2)2
(1)求证{an}是等差数列
(2)若bn＝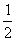
an－30，求数列{bn}的前n项和的最小值．
查看答案和解析>>
科目：gzsx
来源：数学教研室
题型：044
已知在正整数数列{an}中，前n项和Sn满足：Sn＝
(an＋2)2
(1)求证{an}是等差数列
(2)若bn＝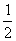
an－30，求数列{bn}的前n项和的最小值．
查看答案和解析>>
科目：gzsx
来源：不详
题型：解答题
数列{an}中，前n项和Sn=2n-1，求证：{an}是等比数列．
查看答案和解析>>
科目：gzsx
来源：2012-2013学年陕西省榆林实验中学高二（上）期末数学试卷（文科）（解析版）
题型：解答题
数列{an}中，前n项和Sn=3n+1，
（1）求a1；
（2）求通项公式an；
（3）该数列是等比数列吗？如不是，请说明理由；如是，请给出证明，并求出该等比数列的公比．
查看答案和解析>>
科目：gzsx
来源：2012年江苏省盐城市东台中学高三数学专项训练：数列（2）（解析版）
题型：填空题
数列{an}中，前n项和Sn=2n（n为正整数），则an= ．
查看答案和解析>>
