
科目:czsx 来源: 题型:
科目:czsx 来源:2010年广东省广州市天秀中学中考数学模拟试卷(解析版) 题型:解答题
科目:czsx 来源: 题型:解答题
科目:czsx 来源: 题型:
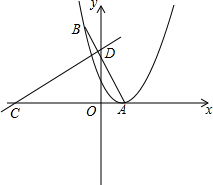 (2012•江汉区模拟)已知:抛物线F1:y=x2+mx+n的顶点为A(1,0)
(2012•江汉区模拟)已知:抛物线F1:y=x2+mx+n的顶点为A(1,0)| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
科目:czsx 来源: 题型:解答题
 已知:抛物线
已知:抛物线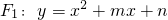 的顶点为A(1,0)
的顶点为A(1,0)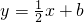 交x轴于点C,交y轴于点D,在抛物线F1上有一点B,且点B与点A关于直线
交x轴于点C,交y轴于点D,在抛物线F1上有一点B,且点B与点A关于直线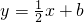 对称,若抛物线F2的顶点为点B,且经过点A,试求抛物线F2的函数解析式;
对称,若抛物线F2的顶点为点B,且经过点A,试求抛物线F2的函数解析式; ?若存在试求n的值;若不存在,请说明理由.
?若存在试求n的值;若不存在,请说明理由.科目:czsx 来源:2013-2014学年江苏省无锡市崇安区九年级上学期期末考试数学试卷(解析版) 题型:解答题
抛物线y=ax2+2x+c与其对称轴相交于点A(1,4),与x轴正半轴交于点B.
(1)求这条抛物线的函数关系式;
(2)在抛物线对称轴上确定一点C,使△ABC是等腰三角形,求出所有点C的坐标.
科目:czsx 来源:2012年湖北省武汉市江汉区中考数学模拟试卷(解析版) 题型:解答题
 的顶点为A(1,0)
的顶点为A(1,0) 交x轴于点C,交y轴于点D,在抛物线F1上有一点B,且点B与点A关于直线
交x轴于点C,交y轴于点D,在抛物线F1上有一点B,且点B与点A关于直线 对称,若抛物线F2的顶点为点B,且经过点A,试求抛物线F2的函数解析式;
对称,若抛物线F2的顶点为点B,且经过点A,试求抛物线F2的函数解析式; ?若存在试求n的值;若不存在,请说明理由.
?若存在试求n的值;若不存在,请说明理由.
科目:czsx 来源: 题型:
 合),过点P分别向x轴、y轴作垂线,垂足分别为C、D.设OC=x,四边形OCPD的面积为S.
合),过点P分别向x轴、y轴作垂线,垂足分别为C、D.设OC=x,四边形OCPD的面积为S.| 3 |
| 4 |
| 9 |
| 8 |
科目:czsx 来源: 题型:
 25、实验与探究:
25、实验与探究:科目:czsx 来源: 题型:解答题
 合),过点P分别向x轴、y轴作垂线,垂足分别为C、D.设OC=x,四边形OCPD的面积为S.
合),过点P分别向x轴、y轴作垂线,垂足分别为C、D.设OC=x,四边形OCPD的面积为S. 时,S有最大值
时,S有最大值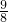 ,求直线AB的解析式;
,求直线AB的解析式;科目:czsx 来源:2012年北京市顺义区中考数学二模试卷(解析版) 题型:解答题
 时,S有最大值
时,S有最大值 ,求直线AB的解析式;
,求直线AB的解析式;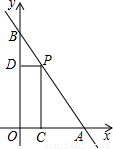
科目:czsx 来源: 题型:
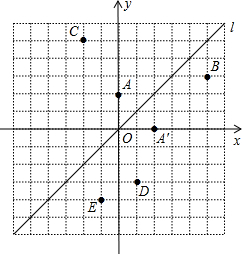
如图,在平面直角坐标系中,直线l是第一、三象限的角平分线.
实验与探究:
(1) 由图观察易知A(0,2)关于直线l的对称点![]() 的坐标为(2,0),请在图中分别标明B(5,3) 、C(-2,5) 关于直线l的对称点
的坐标为(2,0),请在图中分别标明B(5,3) 、C(-2,5) 关于直线l的对称点![]() 、
、![]() 的位置,并写出他们的坐标:
的位置,并写出他们的坐标:
![]() ( )、
( )、 ![]() ( );(4分)
( );(4分)
归纳与发现:
(2) 结合图形观察以上三组点的坐标,你会发现:坐标平面内任一点P(a,b)关于第一、三象限的角平分线l的对称点![]() 的坐标为( )(不必证明);(2分)
的坐标为( )(不必证明);(2分)
运用与拓广:
(3) 已知两点D(1,-3)、E(-1,-4),试在直线l上确定一点Q,使点Q到D、E两点的距离之和最小.(要有必要的画图说明)(3分)
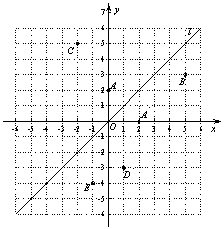 |
科目:czsx 来源: 题型:解答题
 实验与探究:
实验与探究:科目:czsx 来源: 题型:
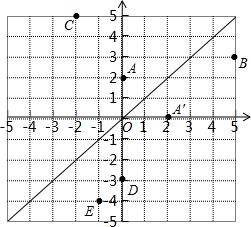 如图,在平面直角坐标系中,函数y=x的图象l是第一、三象限的角平分线.
如图,在平面直角坐标系中,函数y=x的图象l是第一、三象限的角平分线.科目:czsx 来源: 题型:
科目:czsx 来源: 题型:
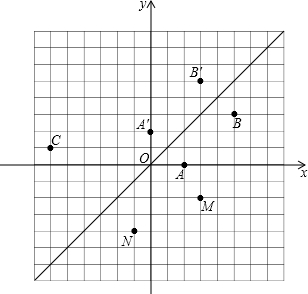 如图,在平面直角坐标系中,直线L:y=x是第一、三象限的角平分线.
如图,在平面直角坐标系中,直线L:y=x是第一、三象限的角平分线.科目:czsx 来源: 题型:
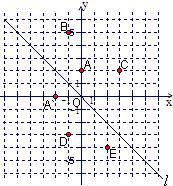 如图,在平面直角坐标系中,直线l是第二、四象限的角平分线.
如图,在平面直角坐标系中,直线l是第二、四象限的角平分线.