
科目:czsx 来源: 题型:
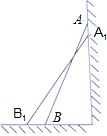 子的顶端沿墙下滑0.4米,那么点B将向外移动多少米?
子的顶端沿墙下滑0.4米,那么点B将向外移动多少米?| 2.52-0.72 |
| B | 2 1 |
科目:czsx 来源: 题型:
 s,则s与x的函数关系式为:s=-x2+
s,则s与x的函数关系式为:s=-x2+| 1 |
| 2 |
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
| x | … |
|
|
|
1 | 2 | 3 | 4 | … | ||||||
| y | … | … |
| 1 |
| x |
| 1 |
| 2 |
| 1 |
| x |
| x |
科目:czsx 来源: 题型:阅读理解
| y |
| 2 |
| y |
| 2 |
| y |
| 2 |
| y |
| 2 |
科目:czsx 来源: 题型:阅读理解

科目:czsx 来源: 题型:
科目:czsx 来源: 题型:
 (2012•镇江)对于二次函数y=x2-3x+2和一次函数y=-2x+4,把y=t(x2-3x+2)+(1-t)(-2x+4)称为这两个函数的“再生二次函数”,其中t是不为零的实数,其图象记作抛物线E.
(2012•镇江)对于二次函数y=x2-3x+2和一次函数y=-2x+4,把y=t(x2-3x+2)+(1-t)(-2x+4)称为这两个函数的“再生二次函数”,其中t是不为零的实数,其图象记作抛物线E.科目:czsx 来源:2012-2013学年江苏省南京市鼓楼区中考二模数学试卷(解析版) 题型:解答题
【提出问题】
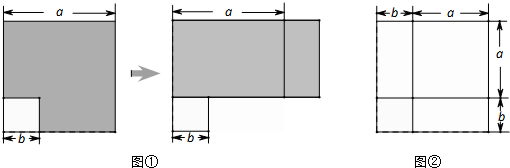
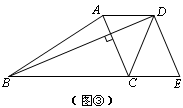
如图①,在梯形ABCD中,AD//BC,AC、BD交于点E,∠BEC=n°,若AD=a,BC=b,则梯形ABCD的面积最大是多少?
【探究过程】
小明提出:可以从特殊情况开始探究,如图②,在梯形ABCD中,AD//BC,AC⊥BD,若AD=3,BC=7,则梯形ABCD的面积最大是多少?
如图③,过点D做DE//AC交BC的延长线于点E,那么梯形ABCD的面积就等于△DBE的面积,求梯形ABCD的面积最大值就是求△DBE的面积最大值.如果设AC=x,BD=y,那么S△DBE=xy.
以下是几位同学的对话:
A同学:因为y=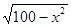 ,所以S△DBE=x
,所以S△DBE=x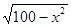 ,求这个函数的最大值即可.
,求这个函数的最大值即可.
B同学:我们知道x2+y2=100,借助完全平方公式可求S△DBE=xy的最大值
C同学:△DBE是直角三角形,底BE=10,只要高最大,S△DBE就最大,我们先将所有满足BE=10的直角△DBE都找出来,然后在其中寻找高最大的△DBE即可.

(1)请选择A同学或者B同学的方法,完成解题过程.
(2)请帮C同学在图③中画出所有满足条件的点D,并标出使△DBE面积最大的点D1.(保留作图痕迹,可适当说明画图过程)
【解决问题】
根据对特殊情况的探究经验,请在图①中画出面积最大的梯形ABCD的顶点D1,并直接写出梯形ABCD面积的最大值.
科目:czsx 来源:2012年初中毕业升学考试(浙江绍兴卷)数学(带解析) 题型:解答题
小明和同桌小聪在课后复习时,对课本“目标与评定”中的一道思考题,进行了认真的探索。
【思考题】如图,一架2.5米长的梯子AB斜靠在竖直的墙AC上,这时B到墙C的距离为0.7米,如果梯子的顶端沿墙下滑0.4米,那么点B将向外移动多少米?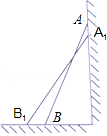
(1)请你将小明对“思考题”的解答补充完整:
解:设点B将向外移动x米,即BB1=x,
则B1C=x+0.7,A1C=AC﹣AA1=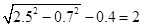
而A1B1=2.5,在Rt△A1B1C中,由 得方程 ,
得方程 ,
解方程得x1= ,x2= ,
∴点B将向外移动 米。
(2)解完“思考题”后,小聪提出了如下两个问题:
【问题一】在“思考题”中,将“下滑0.4米”改为“下滑0.9米”,那么该题的答案会是0.9米吗?为什么?
【问题二】在“思考题”中,梯子的顶端从A处沿墙AC下滑的距离与点B向外移动的距离,有可能相等吗?为什么?
请你解答小聪提出的这两个问题。
科目:czsx 来源:2012年江苏省镇江市中考数学试卷(解析版) 题型:解答题

科目:czsx 来源:2013届江苏省南京市鼓楼区中考二模数学试卷(带解析) 题型:解答题
【提出问题】
如图①,在梯形ABCD中,AD//BC,AC、BD交于点E,∠BEC=n°,若AD=a,BC=b,则梯形ABCD的面积最大是多少?
【探究过程】
小明提出:可以从特殊情况开始探究,如图②,在梯形ABCD中,AD//BC,AC⊥BD,若AD=3,BC=7,则梯形ABCD的面积最大是多少?
如图③,过点D做DE//AC交BC的延长线于点E,那么梯形ABCD的面积就等于△DBE的面积,求梯形ABCD的面积最大值就是求△DBE的面积最大值.如果设AC=x,BD=y,那么S△DBE=xy.
以下是几位同学的对话:
A同学:因为y=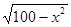 ,所以S△DBE=x
,所以S△DBE=x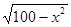 ,求这个函数的最大值即可.
,求这个函数的最大值即可.
B同学:我们知道x2+y2=100,借助完全平方公式可求S△DBE=xy的最大值
C同学:△DBE是直角三角形,底BE=10,只要高最大,S△DBE就最大,我们先将所有满足BE=10的直角△DBE都找出来,然后在其中寻找高最大的△DBE即可.

(1)请选择A同学或者B同学的方法,完成解题过程.
(2)请帮C同学在图③中画出所有满足条件的点D,并标出使△DBE面积最大的点D1.(保留作图痕迹,可适当说明画图过程)
【解决问题】
根据对特殊情况的探究经验,请在图①中画出面积最大的梯形ABCD的顶点D1,并直接写出梯形ABCD面积的最大值.
科目:czsx 来源:2013年初中毕业升学考试(四川泸州卷)数学(解析版) 题型:选择题
(2013年四川泸州2分)设x1、x2是方程x2+3x﹣3=0的两个实数根,则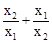 的值为【 】
的值为【 】
A.5 B.﹣5 C.1 D.﹣1
科目:czsx 来源: 题型:
二、函数的定义域、值域及单调性
【例2】 (1)已知f(x)的定义域为[1,2),求函数f(x2)的定义域;
(2)已知f(x+1)的定义域为[0,1],求函数f(x)的定义域.
解:(1)由f(x)的定义域为[1,2),
可知f(x2)中自变量x2也应在[1,2)中,
故1≤x2<2,∴-![]() <x≤-1或1≤x<
<x≤-1或1≤x<![]() ,
,
即f(x2)的定义域为(-![]() ,-1]∪[1,
,-1]∪[1, ![]() ).
).
(2)已知f(x)的定义域为[0,1],即0≤x≤1,
则1≤x+1≤2,∴f(x)的定义域为[1,2].
科目:czsx 来源:2007年广东省深圳市东湖中学九年级数学竞赛试卷(解析版) 题型:解答题
科目:czsx 来源: 题型:
【例3】 设函数f(x)= ![]() -ax,其中a>0,求a的取值范围,使函数f(x)在[0,+∞)上为单调函数.
-ax,其中a>0,求a的取值范围,使函数f(x)在[0,+∞)上为单调函数.
解:任取x1、x2∈[0,+∞)且x1<x2,则
f(x1)-f(x2)=![]() -
-![]() -a(x1-x2)
-a(x1-x2)
=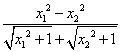 -a(x1-x2)
-a(x1-x2)
=(x1-x2)(![]() -a).
-a).
(1)当a≥1时,∵![]() <1,
<1,
又∵x1-x2<0,
∴f(x1)-f(x2)>0,即f(x1)>f(x2).
∴a≥1时,函数f(x)在区间[0,+∞)上为减函数.
(2)当0<a<1时,在区间[0,+∞)上存在x1=0,x2=![]() ,满足f(x1)=f(x2)=1,
,满足f(x1)=f(x2)=1,
∴0<a<1时,f(x)在[0,+∞)上不是单调函数.
评注: ①判断单调性常规思路为定义法;②变形过程中![]() <1利用了
<1利用了![]() >|x1|≥x1,
>|x1|≥x1, ![]() >x2这个结论;③从a的范围看还需讨论0<a<1时f(x)的单调性,这也是数学严谨性的体现.
>x2这个结论;③从a的范围看还需讨论0<a<1时f(x)的单调性,这也是数学严谨性的体现.
科目:czsx 来源:2013年山东省青岛市中考数学试卷(解析版) 题型:解答题

科目:czsx 来源:《第2章 二次函数》2010年单元测验(解析版) 题型:解答题
科目:czsx 来源: 题型:
二、函数的定义域、值域及单调性
【例2】 (1)已知f(x)的定义域为[1,2),求函数f(x2)的定义域;
(2)已知f(x+1)的定义域为[0,1],求函数f(x)的定义域.
解:(1)由f(x)的定义域为[1,2),
可知f(x2)中自变量x2也应在[1,2)中,
故1≤x2<2,∴-![]() <x≤-1或1≤x<
<x≤-1或1≤x<![]() ,
,
即f(x2)的定义域为(-![]() ,-1]∪[1,
,-1]∪[1, ![]() ).
).
(2)已知f(x)的定义域为[0,1],即0≤x≤1,
则1≤x+1≤2,∴f(x)的定义域为[1,2].
科目:czsx 来源: 题型:
【例3】 设函数f(x)= ![]() -ax,其中a>0,求a的取值范围,使函数f(x)在[0,+∞)上为单调函数.
-ax,其中a>0,求a的取值范围,使函数f(x)在[0,+∞)上为单调函数.
解:任取x1、x2∈[0,+∞)且x1<x2,则
f(x1)-f(x2)=![]() -
-![]() -a(x1-x2)
-a(x1-x2)
= -a(x1-x2)
-a(x1-x2)
=(x1-x2)(![]() -a).
-a).
(1)当a≥1时,∵![]() <1,
<1,
又∵x1-x2<0,
∴f(x1)-f(x2)>0,即f(x1)>f(x2).
∴a≥1时,函数f(x)在区间[0,+∞)上为减函数.
(2)当0<a<1时,在区间[0,+∞)上存在x1=0,x2=![]() ,满足f(x1)=f(x2)=1,
,满足f(x1)=f(x2)=1,
∴0<a<1时,f(x)在[0,+∞)上不是单调函数.
评注: ①判断单调性常规思路为定义法;②变形过程中![]() <1利用了
<1利用了![]() >|x1|≥x1,
>|x1|≥x1, ![]() >x2这个结论;③从a的范围看还需讨论0<a<1时f(x)的单调性,这也是数学严谨性的体现.
>x2这个结论;③从a的范围看还需讨论0<a<1时f(x)的单调性,这也是数学严谨性的体现.
科目:czsx 来源:2012年浙江省绍兴市中考数学试卷(解析版) 题型:解答题
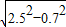 -0.4=2
-0.4=2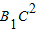 +
+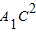 =
=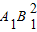 得方程______,
得方程______,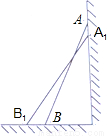
科目:czsx 来源: 题型:
【例3】 设函数f(x)= ![]() -ax,其中a>0,求a的取值范围,使函数f(x)在[0,+∞)上为单调函数.
-ax,其中a>0,求a的取值范围,使函数f(x)在[0,+∞)上为单调函数.
解:任取x1、x2∈[0,+∞)且x1<x2,则
f(x1)-f(x2)=![]() -
-![]() -a(x1-x2)
-a(x1-x2)
= -a(x1-x2)
-a(x1-x2)
=(x1-x2)(![]() -a).
-a).
(1)当a≥1时,∵![]() <1,
<1,
又∵x1-x2<0,
∴f(x1)-f(x2)>0,即f(x1)>f(x2).
∴a≥1时,函数f(x)在区间[0,+∞)上为减函数.
(2)当0<a<1时,在区间[0,+∞)上存在x1=0,x2=![]() ,满足f(x1)=f(x2)=1,
,满足f(x1)=f(x2)=1,
∴0<a<1时,f(x)在[0,+∞)上不是单调函数.
评注: ①判断单调性常规思路为定义法;②变形过程中![]() <1利用了
<1利用了![]() >|x1|≥x1,
>|x1|≥x1, ![]() >x2这个结论;③从a的范围看还需讨论0<a<1时f(x)的单调性,这也是数学严谨性的体现.
>x2这个结论;③从a的范围看还需讨论0<a<1时f(x)的单调性,这也是数学严谨性的体现.