练习册

  • 练习册
  • 试题
    精英家教网 > 试题搜索列表 >已知，如图，在△ABC中，∠BAC=90°，BD平分∠ABC，DE⊥BC与E，证明，BD垂直于AE

    已知，如图，在△ABC中，∠BAC=90°，BD平分∠ABC，DE⊥BC与E，证明，BD垂直于AE答案解析

    科目：czsx 来源： 题型：

    精英家教网已知：如图，在▱ABCD中，BE、CE分别平分∠ABC、∠BCD，E在AD上，BE=12cm，CE=5cm．求▱ABCD的周长和面积．

    查看答案和解析>>

    科目：czsx 来源： 题型：解答题

    已知：如图，在▱ABCD中，BE、CE分别平分∠ABC、∠BCD，E在AD上，BE=12 cm，CE=5 cm．求▱ABCD的周长和面积．

    查看答案和解析>>

    科目：czsx 来源：2011-2012学年安徽省淮北二中九年级（上）第一次月考数学试卷（解析版） 题型：解答题

    已知：如图，在▱ABCD中，BE、CE分别平分∠ABC、∠BCD，E在AD上，BE=12 cm，CE=5 cm．求▱ABCD的周长和面积．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    已知：如图，在□ABCD中，BE、CE分别平分∠ABC、∠BCD，E在AD上，

    BE＝12 cm，CE＝5 cm．求□ABCD的周长和面积．

    查看答案和解析>>

    科目：czsx 来源： 题型：

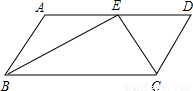
    已知，如图，在△ADC中，∠ADC=90°，以DC为直径作半圆⊙O，交边AC于点F，点B在CD的延长线上，连接BF，交AD于点E，∠BED=2∠C．
    （1）求证：BF是⊙O的切线；
    （2）若BF=FC，AE=
    		3
    ，求⊙O的半径．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    15、已知：如图，在▱ABCD中，对角线AC、BD相交于点O，AE⊥BD，CF⊥BD，垂足分别为E、F．
    求证：四边形AECF是平行四边形．

    查看答案和解析>>

    科目：czsx 来源： 题型：

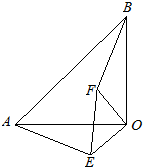    31、已知：如图，在△OAB中，∠AOB=90°，OA=OB，在△EOF中，∠EOF=90°，OE=OF，连接AE、BF．问线段AE与BF之间有什么关系？请说明理由．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    24、已知：如图，在▱ABCD中，对角线AC交BD于点O，四边形AODE是平行四边形．求证：四边形ABOE、四边形DCOE都是平行四边形．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    已知，如图，在△ADC中，∠ADC=90°，∠A=60°，以DC为直径作半圆⊙O，交边AC于点F，点B在CD的延长线上，连接BF，交AD于点E，BF=FC．
    （1）求证：BF是⊙O的切线；
    （2）若AE=
    		3
    ，求⊙O的半径．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    已知：如图①，在▱ABCD中，O为对角线BD的中点．过O的直线MN交直线AB于点M，交直线CD于点N；过O的另一条直线PQ交直线AD于点P，交直线BC于点Q，连接PN、MQ．
    精英家教网精英家教网
    （1）试证明△PON与△QOM全等；
    （2）若点O为直线BD上任意一点，其他条件不变，则△PON与△QOM又有怎样的关系？试就点O在图②所示的位置，画出图形，证明你的猜想；
    （3）若点O为直线BD上任意一点（不与点B、D重合），设OD：OB=k，PN=x，MQ=y，则y与x之间的函数关系式为
     
    ．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    （2013•太原二模）已知：如图，在▱ABCD中，对角线AC、BD相交于点O，EF过点O分别交AD、BC于点E、F．
    求证：OE=OF．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    已知：如图，在▱ABCD中，对角线AC交BD于点O，四边形AODE是平行四边形．
    求证：四边形ABOE是平行四边形．

    查看答案和解析>>

    科目：czsx 来源： 题型：

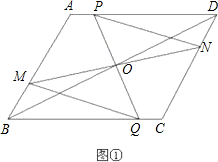
    24、已知：如图，梯形ABCD中，AD∥BC，BD平分∠ABC，E、F分别为AD、AB中点，G为BC边上一点，且GE=GF．
    （1）求证：∠AEG=∠AFG；
    （2）猜想：当AB=
    2
    GC时，四边形GCDE为平行四边形，并说明理由．

    查看答案和解析>>

    科目：czsx 来源： 题型：

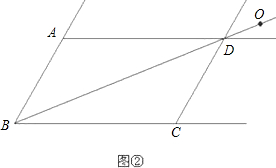
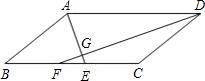    精英家教网已知：如图，在▱ABCD中，∠ADC、∠DAB的平分线DF、AE分别与线段BC相交于点F、E，DF与AE相交于点G．
    （1）求证：AE⊥DF；
    （2）若AD=10，AB=6，AE=4，求DF的长．

    查看答案和解析>>

    科目：czsx 来源：2014届江苏省太仓市七年级下学期期中考试数学试卷（解析版） 题型：解答题

    探究与发现：

    探究一：我们知道，三角形的一个外角等于与它不相邻的两个内角的和．那么，三角形的一个内角与它不相邻的两个外角的和之间存在何种数量关系呢？

    已知：如图，∠FDC与∠ECD分别为△ADC的两个外角，

    试探究∠A与∠FDC+∠ECD的数量关系．

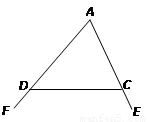
    探究二：三角形的一个内角与另两个内角的平分线所夹的钝角之间有何种关系？

    已知：如图，在△ADC中，DP、CP分别平分∠ADC和∠ACD，试探究∠P与∠A的数量关系．

    探究三：若将△ADC改为任意四边形ABCD呢？

    已知：如图，在四边形ABCD中，DP、CP分别平分∠ADC和∠BCD，试利用上述结论探究∠P与∠A+∠B的数量关系．

    探究四：若将上题中的四边形ABCD改为六边形ABCDEF呢？

    请直接写出∠P与∠A+∠B+∠E+∠F的数量关系： _______________________________．

     

     

    查看答案和解析>>

    科目：czsx 来源：2011-2012学年江苏省太仓市七年级下学期期中考试数学试卷（带解析） 题型：解答题

    探究与发现：
    探究一：我们知道，三角形的一个外角等于与它不相邻的两个内角的和．那么，三角形的一个内角与它不相邻的两个外角的和之间存在何种数量关系呢？
    已知：如图，∠FDC与∠ECD分别为△ADC的两个外角，
    试探究∠A与∠FDC+∠ECD的数量关系．

    探究二：三角形的一个内角与另两个内角的平分线所夹的钝角之间有何种关系？
    已知：如图，在△ADC中，DP、CP分别平分∠ADC和∠ACD，试探究∠P与∠A的数量关系．

    探究三：若将△ADC改为任意四边形ABCD呢？
    已知：如图，在四边形ABCD中，DP、CP分别平分∠ADC和∠BCD，试利用上述结论探究∠P与∠A+∠B的数量关系．

    探究四：若将上题中的四边形ABCD改为六边形ABCDEF呢？
    请直接写出∠P与∠A+∠B+∠E+∠F的数量关系： _______________________________．

    查看答案和解析>>

    科目：czsx 来源：2014届江苏省太仓市七年级期中考试数学卷（解析版） 题型：解答题

    探究与发现：

    探究一：我们知道，三角形的一个外角等于与它不相邻的两个内角的和．那么，三角形的一个内角与它不相邻的两个外角的和之间存在何种数量关系呢？已知：如图，∠FDC与∠ECD分别为△ADC的两个外角，试探究∠A与∠FDC+∠ECD的数量关系．

     

    探究二：三角形的一个内角与另两个内角的平分线所夹的钝角之间有何种关系？

    已知：如图，在△ADC中，DP、CP分别平分∠ADC和∠ACD，试探究∠P与∠A的数量关系．

    探究三：若将△ADC改为任意四边形ABCD呢？

    已知：如图，在四边形ABCD中，DP、CP分别平分∠ADC和∠BCD，试利用上述结论探究∠P与∠A+∠B的数量关系．

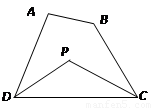
    探究四：若将上题中的四边形ABCD改为六边形ABCDEF呢？

    请直接写出∠P与∠A+∠B+∠E+∠F的数量关系：_______________________________．

     

    查看答案和解析>>

    科目：czsx 来源： 题型：解答题

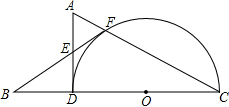    作业宝已知，如图，在△ADC中，∠ADC=90°，∠A=60°，以DC为直径作半圆⊙O，交边AC于点F，点B在CD的延长线上，连接BF，交AD于点E，BF=FC．
    （1）求证：BF是⊙O的切线；
    （2）若AE=数学公式，求⊙O的半径．

    查看答案和解析>>

    科目：czsx 来源：2011-2012学年江苏省太仓市七年级期中考试数学卷（带解析） 题型：解答题

    探究与发现：
    探究一：我们知道，三角形的一个外角等于与它不相邻的两个内角的和．那么，三角形的一个内角与它不相邻的两个外角的和之间存在何种数量关系呢？已知：如图，∠FDC与∠ECD分别为△ADC的两个外角，试探究∠A与∠FDC+∠ECD的数量关系．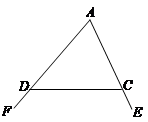

    探究二：三角形的一个内角与另两个内角的平分线所夹的钝角之间有何种关系？
    已知：如图，在△ADC中，DP、CP分别平分∠ADC和∠ACD，试探究∠P与∠A的数量关系．

    探究三：若将△ADC改为任意四边形ABCD呢？
    已知：如图，在四边形ABCD中，DP、CP分别平分∠ADC和∠BCD，试利用上述结论探究∠P与∠A+∠B的数量关系．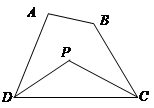

    探究四：若将上题中的四边形ABCD改为六边形ABCDEF呢？
    请直接写出∠P与∠A+∠B+∠E+∠F的数量关系：_______________________________．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    已知：如图，在□ABCD中，对角线AC交BD于点O，四边形AODE是平行四边形。求证：四边形ABOE、四边形DCOE都是平行四边形。

     


    查看答案和解析>>