精英家教网 >
试题搜索列表 >如图,抛物线y=-x2+bx+c与x轴负半轴交于点A,与y轴正是假的就看空间将半轴
如图,抛物线y=-x2+bx+c与x轴负半轴交于点A,与y轴正是假的就看空间将半轴答案解析
科目:czsx
来源:
题型:

如图,抛物线y=x
2+bx+c与x轴交于A(-1,0),B(3,0)两点.
(1)求b、c的值;
(2)P为抛物线上的点,且满足S
△PAB=8,求P点的坐标;
(3)设抛物线交y 轴于C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:

(2013•清远模拟)如图,抛物线y=-x
2+bx+c与x轴交于A、B两点,与y轴交于点D,其顶点为C,已知A、D两点的坐标分别为A(-1,0),D(0,3),
①求该抛物线的表达式;
②△AOD与△BCD是否相似?若相似请加以证明;若不相似,请说明理由.
③抛物线上有一动点P,点P在第一象限且在对称轴的右侧,问是否存在这样的点P,使四边形APCD的面积等于4?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:

(2012•连云港)如图,抛物线y=-x
2+bx+c与x轴交于A、B两点,与y轴交于点C,点O为坐标原点,点D为抛物线的顶点,点E在抛物线上,点F在x轴上,四边形OCEF为矩形,且OF=2,EF=3,
(1)求抛物线所对应的函数解析式;
(2)求△ABD的面积;
(3)将△AOC绕点C逆时针旋转90°,点A对应点为点G,问点G是否在该抛物线上?请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:

8、如图,抛物线y=x
2+bx+c与x轴交于A、B两点,与y轴交于点C,且∠OBC=45°,则下列各式成立的是( )
查看答案和解析>>
科目:czsx
来源:
题型:
(2013•河南)如图,抛物线y=-x
2+bx+c与直线y=
x+2交于C、D两点,其中点C在y轴上,点D的坐标为(3,
).点P是y轴右侧的抛物线上一动点,过点P作PE⊥x轴于点E,交CD于点F.
(1)求抛物线的解析式;
(2)若点P的横坐标为m,当m为何值时,以O、C、P、F为顶点的四边形是平行四边形?请说明理由.
(3)若存在点P,使∠PCF=45°,请直接写出相应的点P的坐标.

查看答案和解析>>
科目:czsx
来源:
题型:

已知,如图,抛物线y=-x
2+bx+c与x轴,y轴分别相交于点A(-1,0),B(0,3)两点,其顶点为D
(1)求该抛物线的解析式;
(2)若抛物线与x轴另一个交点为E,求四边形ABDE的面积.
查看答案和解析>>
科目:czsx
来源:
题型:
已知:如图,抛物线y=-x
2+bx+c与x轴、y轴分别相交于点A(-1,0)、B(0,3)两点,其顶点为D,与x轴
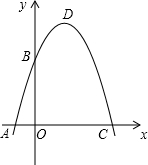
的另一个交点为C.
(1)求该抛物线的解析式;
(2)求四边形ABDC的面积;
(3)判断△DBC的形状,并探讨:△AOB与△BDC是否相似?如果相似,请证明;否则,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:

如图,抛物线y=-x
2+bx+c与x轴交与A(1,O),B(-4,0)两点.
(1)求该抛物线的解析式;
(2)设(1)中的抛物线交y轴于C点,在该抛物线的对称轴上找一点Q,使得△QAC的周长最小,请求出Q点的坐标;
(3)设平行于y轴的直线x=m(-1-
<m<0)与抛物线交于点M,与直线y=-x交于点N.连结BM、CM、NC、NB,问是否存在m的值,使四边形BNCM的面积S最大?若存在,请求出m的值;若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
已知:如图,抛物线y=-x
2+bx+c与x轴、y轴分别相交于点A(-1,0)、B(0,3

)两点,其顶点为D.
(1)求该抛物线的解析式;
(2)若该抛物线与x轴的另一个交点为E.求四边形ABDE的面积;
(3)△AOB与△BDE是否相似?如果相似,请予以证明;如果不相似,请说明理由.
(注:抛物线y=ax
2+bx+c(a≠0)的顶点坐标为
(-,))
查看答案和解析>>
科目:czsx
来源:
题型:

如图,抛物线y=x
2+bx+c与x轴交于A(-1,0),B(3,0)两点.
(1)求b、c的值;
(2)P为抛物线上的点,且满足S
△PAB=8,求P点的坐标.
查看答案和解析>>
科目:czsx
来源:
题型:
如图,抛物线y=x
2+bx+c与x轴交于A,B两点,与y轴下半轴交于C点,且经过点(2,-3),抛物线的最小值为-4,顶点是M.
(1)求抛物线对应的函数表达式;
(2)经过C、M两点作直线与x轴交于点N,在抛物线上是否存在这样的点P,使以点P、A、C、N为顶点的四边形为平行四边形?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)设直线y=-x+3与y轴的交点是D,在直线BD上任取一点E(不与B、D重合),经过A、B、E三点
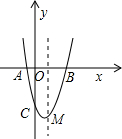
的圆交直线BC于点F,试判断△AEF的形状,并说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:

如图,抛物线y=x
2+bx+c与x轴的负半轴相交于A、B两点,与y轴的正半轴相交于C点,与双曲线y=
的一个交点是(1,m),且OA=OC.求抛物线的解析式.
查看答案和解析>>
科目:czsx
来源:
题型:
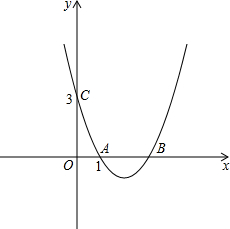
已知:如图,抛物线y=x
2+bx+c与x轴的一个相交点坐标为A(1,0),与y轴上的交点坐标C(0,3).
(1)求抛物线的函数关系式;
(2)求与x轴的另一交点坐标B;
(3)若点D(
,m)是抛物线y=x
2+bx+c上的一点,请求出m的值,并求出此时△ABD的面积.
查看答案和解析>>
科目:czsx
来源:
题型:
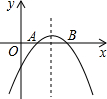
如图,抛物线y=-x
2+bx+c与x轴的两个交点分别为A(1,0),B(3,0).
(1)求这条抛物线对应函数的表达式;
(2)若P点在该抛物线上,求当△PAB的面积为8时,点P的坐标.
查看答案和解析>>
科目:czsx
来源:
题型:
如图,抛物线y=x
2+bx+c与x轴交于A、B两点,与y轴交于点C,D是抛物线

上一点,其坐标为(
,-
),B点坐标为(1,0).
(1)求抛物线的解析式;
(2)经过A、B、D三点的圆交AC于F,交直线y=x+3于点E.试判断△BEF的形状,并加以证明.
查看答案和解析>>
科目:czsx
来源:
题型:
(2013•大连)如图,抛物线y=x
2+bx+
与y轴相交于点A,与过点A平行于x轴的直线相交于点B(点B在第一象限).抛物线的顶点C在直线OB上,对称轴与x轴相交于点D.平移抛物线,使其经过点A、D,则平移后的抛

物线的解析式为
.
查看答案和解析>>
科目:czsx
来源:
题型:

(2010•海沧区质检)如图,抛物线y=x
2+bx+c与x轴的右交点为A,顶点D在矩形OABC的边BC上,当y≤0时,x的取值范围是1≤x≤5.
(1)求b,c的值;
(2)直线y=mx+n经过抛物线的顶点D,该直线在矩形OABC内部分割出的三角形的面积记为S,求S与m的函数关系式,并写出自变量m的取值范围.
查看答案和解析>>
科目:czsx
来源:
题型:
(2012•赤峰)如图,抛物线y=x
2-bx-5与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,点C
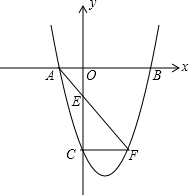
与点F关于抛物线的对称轴对称,直线AF交y轴于点E,|OC|:|OA|=5:1.
(1)求抛物线的解析式;
(2)求直线AF的解析式;
(3)在直线AF上是否存在点P,使△CFP是直角三角形?若存在,求出P点坐标;若不存在,说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
如图,抛物线y=-x
2+bx+c与x轴的一个交点是A,与y轴的交点是B,且OA、OB(OA<OB)
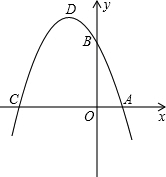
的长是方程x
2-6x+5=0的两个实数根.
(1)求A、B两点的坐标;
(2)求出此抛物线的解析式及顶点D的坐标;
(3)求出此抛物线与x轴的另一个交点C的坐标;
(4)在直线BC上是否存在一点P,使四边形PDCO为梯形?若存在,求出P点坐标;若不存在,说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
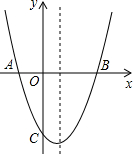
如图,抛物线y=x
2+bx+c与x轴交于A(-1,0),B(3,0)两点.
(1)求该抛物线的解析式;
(2)设(1)题中的抛物线上有一个动点P,当点P在抛物线上滑动到什么位置时,满足S
△PAB=8,并求出此时P点的坐标;
(3)设(1)题中的抛物线交y轴于C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由.
查看答案和解析>>

 如图,抛物线y=x2+bx+c与x轴交于A(-1,0),B(3,0)两点.
如图,抛物线y=x2+bx+c与x轴交于A(-1,0),B(3,0)两点. (2013•清远模拟)如图,抛物线y=-x2+bx+c与x轴交于A、B两点,与y轴交于点D,其顶点为C,已知A、D两点的坐标分别为A(-1,0),D(0,3),
(2013•清远模拟)如图,抛物线y=-x2+bx+c与x轴交于A、B两点,与y轴交于点D,其顶点为C,已知A、D两点的坐标分别为A(-1,0),D(0,3), (2012•连云港)如图,抛物线y=-x2+bx+c与x轴交于A、B两点,与y轴交于点C,点O为坐标原点,点D为抛物线的顶点,点E在抛物线上,点F在x轴上,四边形OCEF为矩形,且OF=2,EF=3,
(2012•连云港)如图,抛物线y=-x2+bx+c与x轴交于A、B两点,与y轴交于点C,点O为坐标原点,点D为抛物线的顶点,点E在抛物线上,点F在x轴上,四边形OCEF为矩形,且OF=2,EF=3,
 已知,如图,抛物线y=-x2+bx+c与x轴,y轴分别相交于点A(-1,0),B(0,3)两点,其顶点为D
已知,如图,抛物线y=-x2+bx+c与x轴,y轴分别相交于点A(-1,0),B(0,3)两点,其顶点为D 的另一个交点为C.
的另一个交点为C. 如图,抛物线y=-x2+bx+c与x轴交与A(1,O),B(-4,0)两点.
如图,抛物线y=-x2+bx+c与x轴交与A(1,O),B(-4,0)两点. )两点,其顶点为D.
)两点,其顶点为D. 如图,抛物线y=x2+bx+c与x轴交于A(-1,0),B(3,0)两点.
如图,抛物线y=x2+bx+c与x轴交于A(-1,0),B(3,0)两点.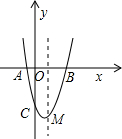 的圆交直线BC于点F,试判断△AEF的形状,并说明理由.
的圆交直线BC于点F,试判断△AEF的形状,并说明理由.  如图,抛物线y=x2+bx+c与x轴的负半轴相交于A、B两点,与y轴的正半轴相交于C点,与双曲线y=
如图,抛物线y=x2+bx+c与x轴的负半轴相交于A、B两点,与y轴的正半轴相交于C点,与双曲线y= 已知:如图,抛物线y=x2+bx+c与x轴的一个相交点坐标为A(1,0),与y轴上的交点坐标C(0,3).
已知:如图,抛物线y=x2+bx+c与x轴的一个相交点坐标为A(1,0),与y轴上的交点坐标C(0,3). 如图,抛物线y=-x2+bx+c与x轴的两个交点分别为A(1,0),B(3,0).
如图,抛物线y=-x2+bx+c与x轴的两个交点分别为A(1,0),B(3,0). 上一点,其坐标为(
上一点,其坐标为( 物线的解析式为
物线的解析式为 (2010•海沧区质检)如图,抛物线y=x2+bx+c与x轴的右交点为A,顶点D在矩形OABC的边BC上,当y≤0时,x的取值范围是1≤x≤5.
(2010•海沧区质检)如图,抛物线y=x2+bx+c与x轴的右交点为A,顶点D在矩形OABC的边BC上,当y≤0时,x的取值范围是1≤x≤5. 与点F关于抛物线的对称轴对称,直线AF交y轴于点E,|OC|:|OA|=5:1.
与点F关于抛物线的对称轴对称,直线AF交y轴于点E,|OC|:|OA|=5:1. 的长是方程x2-6x+5=0的两个实数根.
的长是方程x2-6x+5=0的两个实数根. 如图,抛物线y=x2+bx+c与x轴交于A(-1,0),B(3,0)两点.
如图,抛物线y=x2+bx+c与x轴交于A(-1,0),B(3,0)两点.