
科目:czsx 来源:2011-2012年浙江省衢州华外九年级上学期第二次质量检测数学卷 题型:解答题
(本题10分)问题情境
已知矩形的面积为a(a为常数,a>0),当该矩形的长为多少时,它的周长最小?最小值是多少?
数学模型
设该矩形的一边长为x,周长为y,则y与x的函数关系式为 .
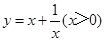 探索研究
探索研究
⑴我们可以借鉴以前研究函数的经验,先探索函数的图象性质.
①填写下表,画出函数的图象:
|
x |
…… |
|
|
|
1 |
2 |
3 |
4 |
…… |
|
y |
…… |
|
|
|
|
|
|
|
…… |

|
③在求二次函数y=ax+bx+c(a≠0)的最大(小)值时,除了通过观察图象,还可以通过
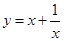
配方得到.请你通过配方求函数(x>0)的最小值.
解决问题
⑵用上述方法解决“问题情境”中的问题,直接写出答案.
科目:czsx 来源:2013-2014学年广东省广州市海珠区九年级上学期期末数学试卷(解析版) 题型:选择题
已知二次函数y=ax²+bx+c(a≠0)的图像如图所示,则下列结论中正确的是( )

A.a>0 B.3是方程ax²+bx+c=0的一个根
C.a+b+c=0 D.当x<1时,y随x的增大而减小
科目:czsx 来源: 题型:
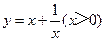
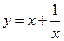
| x | …… | 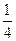 | 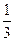 | 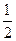 | 1 | 2 | 3 | 4 | …… |
| y | …… | | | | | | | | …… |
|
科目:czsx 来源:2011-2012年浙江省衢州华外九年级上学期第二次质量检测数学卷 题型:解答题
(本题10分)问题情境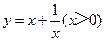

已知矩形的面积为a(a为常数,a>0),当该矩形的长为多少时,它的周长最小?最小值是多少?
数学模型
设该矩形的一边长为x,周长为y,则y与x的函数关系式为 .
探索研究
⑴我们可以借鉴以前研究函数的经验,先探索函数的图象性质.
①填写下表,画出函数的图象:
| x | …… |  |  |  | 1 | 2 | 3 | 4 | …… |
| y | …… | | | | | | | | …… |
|
科目:czsx 来源: 题型:
(本题10分)问题情境
已知矩形的面积为a(a为常数,a>0),当该矩形的长为多少时,它的周长最小?最小值是多少?
数学模型
设该矩形的一边长为x,周长为y,则y与x的函数关系式为 .
![]() 探索研究
探索研究
⑴我们可以借鉴以前研究函数的经验,先探索函数的图象性质.
①填写下表,画出函数的图象:
| x | …… |
|
|
| 1 | 2 | 3 | 4 | …… |
| y | …… |
|
|
|
|
|
|
| …… |
|
③在求二次函数y=ax+bx+c(a≠0)的最大(小)值时,除了通过观察图象,还可以通过
![]()
配方得到.请你通过配方求函数(x>0)的最小值.
解决问题
⑵用上述方法解决“问题情境”中的问题,直接写出答案.
科目:czsx 来源: 题型:
下面是一个二次函数y=ax![]() +bx+c的自变量x和函数y的对应值表:
+bx+c的自变量x和函数y的对应值表:
| x | … | -3 | -2 | -1 | 0 | 1 | 2 | 3 | … |
| y | … | 12 | 5 | 0 | -3 | -4 | -3 | 0 | … |
根据表中提供的信息解答下列各题:
(1)求抛物线与y轴的交点坐标;
(2)抛物线的对称轴是在y轴的右边还是左边?并说明理由
(3)设抛物线与x轴两个交点分别为A、B,顶点为C,求△ABC的面积.
科目:czsx 来源: 题型:
已知二次函数y=ax²+bx+c(c≠0)的图像如图4所示,下列说法错误的是:
(A)图像关于直线x=1对称
(B)函数y=ax²+bx+c(c ≠0)的最小值是 -4
(C)-1和3是方程ax²+bx+c=0(c ≠0)的两个根
(D)当x<1时,y随x的增大而增大
科目:czsx 来源: 题型:
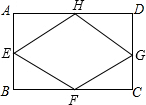 (2013•松北区一模)已知矩形ABCD的周长为12,E、F、G、H为矩形ABCD的各边中点,若AB=x,四边形EFGH的面积为y.
(2013•松北区一模)已知矩形ABCD的周长为12,E、F、G、H为矩形ABCD的各边中点,若AB=x,四边形EFGH的面积为y.| b |
| 2a |
| 4ac-b2 |
| 4a |
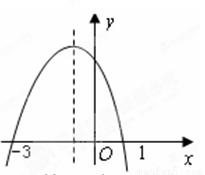
科目:czsx 来源:2013-2014学年山东烟台海阳市九年级上期末数学试卷(解析版) 题型:填空题
二次函数y=ax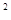 +bx+c的图像如图所示,则不等式ax
+bx+c的图像如图所示,则不等式ax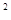 +bx+c>0的解集是
.
+bx+c>0的解集是
.
科目:czsx 来源:2013届黑龙江省哈尔滨市松北区九年级升学调研测试(一)数学试卷(带解析) 题型:解答题
已知矩形ABCD的周长为12,E、F、G、H为矩形ABCD的各边中点,若AB=x,四边形EFGH的面积为y.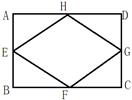
(1)请直接写出y与x的函数关系式;
(2)根据(1)中的函数关系式,计算当x为何值时,y最大,并求出最大值.
(参考公式:当x=- 时,二次函数y=ax+bx+c(a≠o)有最小(大)值
时,二次函数y=ax+bx+c(a≠o)有最小(大)值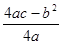 )
)
科目:czsx 来源:2012-2013学年黑龙江省哈尔滨市松北区九年级升学调研测试(一)数学试卷(解析版) 题型:解答题
已知矩形ABCD的周长为12,E、F、G、H为矩形ABCD的各边中点,若AB=x,四边形EFGH的面积为y.

(1)请直接写出y与x的函数关系式;
(2)根据(1)中的函数关系式,计算当x为何值时,y最大,并求出最大值.
(参考公式:当x=- 时,二次函数y=ax+bx+c(a≠o)有最小(大)值
时,二次函数y=ax+bx+c(a≠o)有最小(大)值 )
)
科目:czsx 来源:2012届江苏盐城亭湖区九年级下学期第一次调研考试数学试卷(带解析) 题型:解答题
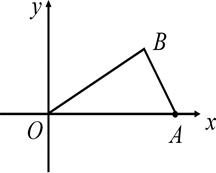
如图11,已知○为坐标原点,∠AOB=30°,∠ABO=90°,且点A的坐标为(2,0).
【小题1】求点B的坐标
【小题2】若二次函数y=ax+bx+c的图象经过A、B、O三点,求此二次函数的解析式;
【小题3】在(2)中的二次函数图象的OB段(不包括点O、B)上,是否存在一点C,使得四边形ABCO的面积最大?若存在,求出这个最大值及此时点C的坐标;若不存在,请说明理由。
科目:czsx 来源: 题型:
科目:czsx 来源:2011-2012学年江苏盐城亭湖区九年级下学期第一次调研考试数学试卷(解析版) 题型:解答题
如图11,已知○为坐标原点,∠AOB=30°,∠ABO=90°,且点A的坐标为(2,0).

1.求点B的坐标
2.若二次函数y=ax+bx+c的图象经过A、B、O三点,求此二次函数的解析式;
3.在(2)中的二次函数图象的OB段(不包括点O、B)上,是否存在一点C,使得四边形ABCO的面积最大?若存在,求出这个最大值及此时点C的坐标;若不存在,请说明理由。
科目:czsx 来源: 题型:
如图11,已知○为坐标原点,∠AOB=30°,∠ABO=90°,且点A的坐标为(2,0).

1.求点B的坐标
2.若二次函数y=ax+bx+c的图象经过A、B、O三点,求此二次函数的解析式;
3.在(2)中的二次函数图象的OB段(不包括点O、B)上,是否存在一点C,使得四边形ABCO的面积最大?若存在,求出这个最大值及此时点C的坐标;若不存在,请说明理由。
科目:czsx 来源: 题型:解答题
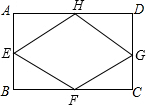 已知矩形ABCD的周长为12,E、F、G、H为矩形ABCD的各边中点,若AB=x,四边形EFGH的面积为y.
已知矩形ABCD的周长为12,E、F、G、H为矩形ABCD的各边中点,若AB=x,四边形EFGH的面积为y. 时,二次函数y=ax+bx+c(a≠0)有最小(大)值
时,二次函数y=ax+bx+c(a≠0)有最小(大)值 )
)科目:czsx 来源: 题型:
若二次函数y=ax+![]() bx+c(a≠0)的图象与x轴有两个交点,坐标分别为(x1,0),(x2,0),且x1<x2,图象上有一点M (x0,y0)在x轴下方,则下列判断中正确的是( ).
bx+c(a≠0)的图象与x轴有两个交点,坐标分别为(x1,0),(x2,0),且x1<x2,图象上有一点M (x0,y0)在x轴下方,则下列判断中正确的是( ).
A.a>0 B.b2-4ac≥0 C. a(x0-x1)( x0-x2)<0 D.x1<x0<x2
科目:czsx 来源: 题型:
若二次函数y=ax+![]() bx+c(a≠0)的图象与x轴有两个交点,坐标分别为(x1,0),(x2,0),且x1<x2,图象上有一点M (x0,y0)在x轴下方,则下列判断中正确的是( ).
bx+c(a≠0)的图象与x轴有两个交点,坐标分别为(x1,0),(x2,0),且x1<x2,图象上有一点M (x0,y0)在x轴下方,则下列判断中正确的是( ).
A.a>0 B.b2-4ac≥0 C. a(x0-x1)( x0-x2)<0 D.x1<x0<x2
科目:czsx 来源: 题型:
二次函数y=ax![]() +bx+c(x≠0)的图象如图所示,若M=a+b-c,N=4a-2b+c,P=2a-b,则M、N、P中,值小于0的数有( )
+bx+c(x≠0)的图象如图所示,若M=a+b-c,N=4a-2b+c,P=2a-b,则M、N、P中,值小于0的数有( )
A、3个 B、2个 C、1个 D、0个
