
科目:czsx 来源:2012届河北省经贸大学附中九年级12月月考数学卷 题型:解答题
(12分)在直角三角形ABC中,角A=90度,AB=8,AC=6,若动点D从点B出发,沿线段BA运动到点A为止,运动速度为每秒钟2个单位长度,过点D作DE平行于BC交于E,设动点D运动的时间为x秒,AE的长为y。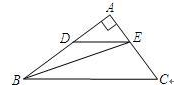
【小题1】(1)求y与x之间的函数关系式,并写出自变量x的取值范围
【小题2】(2)求出△BDE的面积S与x之间的函数关系式;
【小题3】(3)当x为何值时,△BDE的面积S有最大值,最大值为多少?
科目:czsx 来源: 题型:
23、(12分)在直角三角形ABC中,角A=90度,AB=8,AC=6,若动点D从点B出发,沿线段BA运动到点A为止,运动速度为每秒钟2个单位长度,过点D作DE平行于BC交于E,设动点D运动的时间为x秒,AE的长为y。

1.(1)求y与x之间的函数关系式,并写出自变量x的取值范围
2.(2)求出△BDE的面积S与x之间的函数关系式;
3.(3)当x为何值时,△BDE的面积S有最大值,最大值为多少?
科目:czsx 来源: 题型:
科目:czsx 来源:2011-2012学年河北省九年级12月月考数学卷 题型:解答题
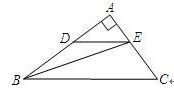
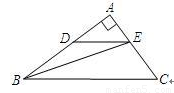
23、(12分)在直角三角形ABC中,角A=90度,AB=8,AC=6,若动点D从点B出发,沿线段BA运动到点A为止,运动速度为每秒钟2个单位长度,过点D作DE平行于BC交于E,设动点D运动的时间为x秒,AE的长为y。
1.(1)求y与x之间的函数关系式,并写出自变量x的取值范围
2.(2)求出△BDE的面积S与x之间的函数关系式;
3.(3)当x为何值时,△BDE的面积S有最大值,最大值为多少?
科目:czsx 来源: 题型:
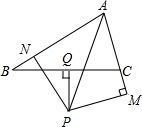 如图,已知在三角形ABC中,角BAC的平分线与BC的垂直平分线PQ相交于点P,过点P分别作PN垂直于AB于点N,PM垂直于AC于点M,求证:BN=CM.
如图,已知在三角形ABC中,角BAC的平分线与BC的垂直平分线PQ相交于点P,过点P分别作PN垂直于AB于点N,PM垂直于AC于点M,求证:BN=CM.科目:czsx 来源:新教材完全解读 八年级数学 (下册) (配人教版新课标) 人教版新课标 题型:013
如图所示,在三角形ABC中,∠C=90°,两直角边AC=6,BC=8,在三角形有一点P,它到各边的距离相等,则这个距离是

A.1
B.2
C.3
D.无法确定
科目:czsx 来源:新课标 1+1轻巧夺冠·优化训练 (人教版)七年级数学(下) 人教版 新课标 银版 题型:044
在三角形ABC中,∠C=90°,则AB2=AC2+BC2,如当AC=6,BC=8时,AB2=62+82=100
∴AB=10(如图)
现已知x轴上一点A(3,0),y轴上一点B(0,-4),连结AB.

求①AB的长②三角形AOB的面积.
科目:czsx 来源: 题型:
(本题满分8分)通过学习三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.类似的,可以在等腰三角形中建立边角之间的联系.我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sad).如图①在△ABC中,AB=AC,顶角A的正对记作sad A,这时sad A![]() .容易知道一个角的大小与这个角的正对值也是相互唯一确定的.根据上述角的正对定义,解下列问题:
.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.根据上述角的正对定义,解下列问题:
(1)sad 60°= .
(2)对于0°<A<180°,∠A的正对值sadA的取值范围是
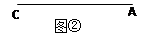
(3)如图②,在Rt△ABC中,∠C=90°,sin A![]() ,试求sad A的值
,试求sad A的值
|
| ||||||||
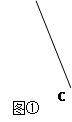 | ||||||||
| ||||||||
科目:czsx 来源: 题型:
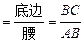 .容易知道一个角的大小与这个角的正对值也是相互唯一确定的.根据上述角的正对定义,解下列问题:
.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.根据上述角的正对定义,解下列问题: ,试求sad A的值
,试求sad A的值
|
 | |||
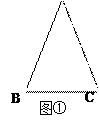 | |||
科目:czsx 来源:2012届江苏省苏州工业园区九年级上学期期中测试数学卷 题型:解答题
(本题满分8分)通过学习三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.类似的,可以在等腰三角形中建立边角之间的联系.我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sad).如图①在△ABC中,AB=AC,顶角A的正对记作sad A,这时sad A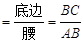 .容易知道一个角的大小与这个角的正对值也是相互唯一确定的.根据上述角的正对定义,解下列问题:
.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.根据上述角的正对定义,解下列问题:
(1)sad 60°= .
(2)对于0°<A<180°,∠A的正对值sad A的取值范围是
(3)如图②,在Rt△ABC中,∠C=90°,sin A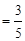 ,试求sad A的值
,试求sad A的值
|
|
||||||||
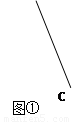 |
||||||||
 |
||||||||
 |
||||||||
|
||||||||
科目:czsx 来源:2011~2012学年江苏省苏州工业园区九年级上学期期中测试数学卷 题型:解答题
(本题满分8分)通过学习三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.类似的,可以在等腰三角形中建立边角之间的联系.我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sad).如图①在△ABC中,AB=AC,顶角A的正对记作sad A,这时sad A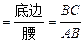 .容易知道一个角的大小与这个角的正对值也是相互
.容易知道一个角的大小与这个角的正对值也是相互 唯一确定的.根据上述角的正对定义,解下列问题:
唯一确定的.根据上述角的正对定义,解下列问题:
(1)sad 60°= .
(2)对于0°<A<180°,∠A的正对值sad A的取值范围是
(3)如图②,在Rt△ABC中,∠C=90°,sin A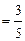 ,试求sad A的值
,试求sad A的值
|
 | |||
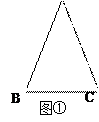 | |||
科目:czsx 来源:学习周报 数学 沪科八年级版 2009-2010学年 第19~26期 总175~182期 沪科版 题型:013
下列说法正确的是
A.在△ABC中,射线AD平分∠BAC,则AD是△ABC的角平分线
B.在△ABC中,M是BC边上的中点,那么直线AM是△ABC的一条中线
C.在Rt△ABC中,∠C=90°,则直角边AC、BC是这个直角三角形的两条高
D.任何三角形的三条高的交点都不可能在这个三角形的外部
科目:czsx 来源:学习周报 数学 沪科九年级版 2009-2010学年 第9期 总第165期 沪科版 题型:022
如图
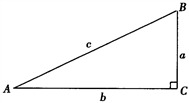
1,在Rt△ABC中,∠C=90°,∠A=30°,∠B=60°.若BC=1,则根据在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半及勾股定理容易得到AB=________,AC=________.因此,含30°角的直角三角形三边(从小到大)之比为________;同样,如图2,含45°角的直角三角形三边(从小到大)之比为________.这样结合三角函数的定义可以推导得到30°、45°、60°角的三角函数值.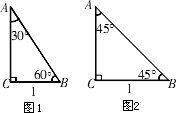
科目:czsx 来源:学习周报 数学 北师大九年级版 2009-2010学年 第14期 总第170期 北师大版 题型:022
如图
1,在Rt△ABC中,∠C=90°,∠A=30°,∠B=60°.若BC=1,则根据“在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半”以及勾股定理容易得到AB=________,AC=________.因此,含30°角的直角三角形三边(从小到大)之比为________;同样,如图2,含45°角的直角三角形三边(从小到大)之比为________.这样结合三角函数的定义可以推导得到30°、45°、60°角的三角函数值.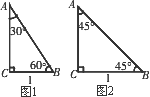
科目:czsx 来源:2008年北京市大兴区初三二模数学试题 题型:044
我们知道:将一条线段AB分割成大小两条线段AC、CB,若小线段CB与大线段AC的长度之比等于大线段AC与线段AB的长度之比,即![]() 这种分割称为黄金分割,点C叫做线段AB的黄金分割点.
这种分割称为黄金分割,点C叫做线段AB的黄金分割点.
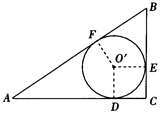
(1)类似地我们可以定义,顶角为36°的等腰三角形叫黄金三角形,其底与腰之比为黄金数,底角平分线与腰的交点为腰的黄金分割点.如图,在△ABC中,∠A=36°,AB=AC,∠ACB的角平分线CD交腰AB于点D,请你说明D为腰AB的黄金分割点的理由.
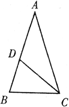
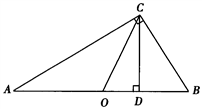
(2)若腰和上底相等,对角线和下底相等的等腰梯形叫作黄金梯形,其对角线的交点为对角线的黄金分割点.如图,AD∥BC,AB=AD=DC,AC=BD=BC,试说明O为AC的黄金分割点.

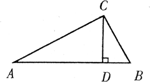
(3)如图,在Rt△ABC中,∠ACB=90°,CD为斜边AB上的高,∠A、∠B、∠ACB的对边分别为a、b、c.若D是AB的黄金分割点,那么a、b、c之间的数量关系是什么?并证明你的结论.
科目:czsx 来源:北京同步题 题型:填空题
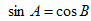 =( )
=( ) 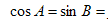 ( )
( )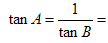 ( )
( )  ( )
( )
科目:czsx 来源:中华题王 数学 七年级上 (人教版) 人教版 题型:044
如图,在三角形ABC中,CD⊥AB于D,∠1+∠3=90°,∠2+∠4=90°,∠1+∠2=90°,请指出图中所有相等的角.

科目:czsx 来源:重庆市重庆一中初2011届九年级3月月考数学试题 题型:044
在Rt△ABC中,∠BAC=90°,三角形的角平分线CE和高AD相交于点F,过F作FG∥BC交AB于点G,求证:(1)AE=BG.(2)若∠B=30°,FD=5,求四边形EBDF的面积.
