精英家教网 >
试题搜索列表 >已知,∠bac=90°,ab=ac,ae=cf,ad⊥be于o,df交be于g.问△efg是什么三角形
已知,∠bac=90°,ab=ac,ae=cf,ad⊥be于o,df交be于g.问△efg是什么三角形答案解析
科目:czsx
来源:
题型:
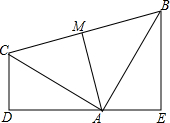
如图所示,已知∠CDA=∠AEB=90°,且CD=AE,AD=BE.问:
(1)AC与AB相等吗?清说明理由;
(2)△ABC是什么三角形?请说明理由;
(3)如果AM⊥BC,则
AM=BC吗?请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:

已知:∠A=90°,AB=AC,BD平分∠ABC,CE⊥BD,垂足为E.求证:BD=2CE.
查看答案和解析>>
科目:czsx
来源:
题型:
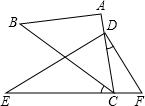
(2013•威海)将一副直角三角板如图摆放,点C在EF上,AC经过点D.已知∠A=∠EDF=90°,AB=AC.∠E=30°,∠BCE=40°,则∠CDF=
25°
25°
.
查看答案和解析>>
科目:czsx
来源:2013年初中毕业升学考试(山东威海卷)数学(解析版)
题型:填空题
将一副直角三角板如图摆放,点C在EF上,AC经过点D.已知∠A=∠EDF=90°,AB=AC.∠E=30°,∠BCE=40°,则∠CDF=
.

查看答案和解析>>
科目:czsx
来源:
题型:解答题
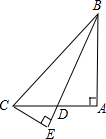 已知:∠A=90°,AB=AC,BD平分∠ABC,CE⊥BD,垂足为E.求证:BD=2CE.
已知:∠A=90°,AB=AC,BD平分∠ABC,CE⊥BD,垂足为E.求证:BD=2CE.
查看答案和解析>>
科目:czsx
来源:甘肃省期中题
题型:证明题
已知:∠A=90°,AB=AC,BD平分∠ABC,CE⊥BD,垂足为E.求证:BD=2CE.
查看答案和解析>>
科目:czsx
来源:
题型:填空题
 将一副直角三角板如图摆放,点C在EF上,AC经过点D.已知∠A=∠EDF=90°,AB=AC.∠E=30°,∠BCE=40°,则∠CDF=________.
将一副直角三角板如图摆放,点C在EF上,AC经过点D.已知∠A=∠EDF=90°,AB=AC.∠E=30°,∠BCE=40°,则∠CDF=________.
查看答案和解析>>
科目:czsx
来源:
题型:
如图(1),已知在△ABC中,AB=AC=10,AD为底边BC上的高,且AD=6.将△ACD沿箭头所示的方向平移,得到△A′CD′.如图(2),A′D′交AB于E,A′C分别交AB、AD于G、F.以D′D为直径作⊙O,设BD′的长为x,⊙O的面积为y.
(1)求y与x之间的函数关系式及自变量x的取值范围;
(2)连接EF,求EF与⊙O相切时x的值;
(3)设四边形ED′DF的面积为S,试求S关于x的函数表达式,并求x为何值时,S的值最大,最大值是多少?
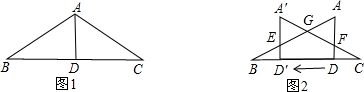
查看答案和解析>>
科目:czsx
来源:
题型:
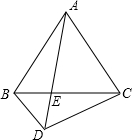
如图,已知四边形ABDC中,AB=AC,对角线AD和BC相交于点E,∠BDA=∠ACB.求证:AB
2=AE•AD.
查看答案和解析>>
科目:czsx
来源:
题型:
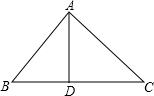
如图,在△ABC中,∠BAC=90°,AB=AC=a,AD是△ABC的高,则AD的长为
.
查看答案和解析>>
科目:czsx
来源:2008年山东省滨州市中考数学试卷(解析版)
题型:解答题
(2008•滨州)如图(1),已知在△ABC中,AB=AC=10,AD为底边BC上的高,且AD=6.将△ACD沿箭头所示的方向平移,得到△A′CD′.如图(2),A′D′交AB于E,A′C分别交AB、AD于G、F.以D′D为直径作⊙O,设BD′的长为x,⊙O的面积为y.
(1)求y与x之间的函数关系式及自变量x的取值范围;
(2)连接EF,求EF与⊙O相切时x的值;
(3)设四边形ED′DF的面积为S,试求S关于x的函数表达式,并求x为何值时,S的值最大,最大值是多少?

查看答案和解析>>
科目:czsx
来源:2013年浙江省中考数学模拟试卷(二)(解析版)
题型:解答题
如图,已知四边形ABDC中,AB=AC,对角线AD和BC相交于点E,∠BDA=∠ACB.求证:AB
2=AE•AD.

查看答案和解析>>
科目:czsx
来源:
题型:
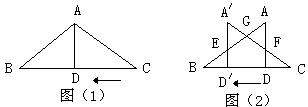
如图(1),已知在△ABC中,AB=AC=10,AD为底边BC上的高,且AD=6。将△ACD沿箭头所示的方向平移,得到△ 。如图(2),
。如图(2), 交AB于E,
交AB于E, 分别交AB.AD于G、F。以
分别交AB.AD于G、F。以 为直径作⊙O,设
为直径作⊙O,设 的长为x,⊙O的面积为y。
的长为x,⊙O的面积为y。
(1)求y与x之间的函数关系式及自变量x的取值范围;
(2)连结EF,求EF与⊙O相切时x的值;
(3)设四边形 的面积为S,试求S关于x的函数表达式,并求x为何值时,S的值最大,最大值是多少?
的面积为S,试求S关于x的函数表达式,并求x为何值时,S的值最大,最大值是多少?
查看答案和解析>>
科目:czsx
来源:专项题
题型:解答题
如图(1),已知在△ABC中,AB=AC=10,AD为底边BC上的高,且AD=6。将△ACD沿箭头所示的方向平移,得到△A′CD′。如图(2),A′D′交AB于E,A′C分别交AB、AD于G、F。以D′D为直径作⊙O,设BD′的长为x,⊙O的面积为y。
(1)求y与x之间的函数关系式及自变量x的取值范围;
(2)连结EF,求EF与⊙O相切时x的值;
(3)设四边形ED′DF的面积为S,试求S关于x的函数表达式,并求x为何值时,S的值最大,最大值是多少?
查看答案和解析>>
科目:czsx
来源:2007年广东省广州市天河区中考数学二模试卷(解析版)
题型:解答题
如图,已知四边形ABDC中,AB=AC,对角线AD和BC相交于点E,∠BDA=∠ACB.求证:AB
2=AE•AD.
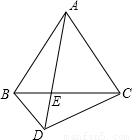
查看答案和解析>>
科目:czsx
来源:第23章《二次函数与反比例函数》中考题集(37):23.5 二次函数的应用(解析版)
题型:解答题
如图(1),已知在△ABC中,AB=AC=10,AD为底边BC上的高,且AD=6.将△ACD沿箭头所示的方向平移,得到△A′CD′.如图(2),A′D′交AB于E,A′C分别交AB、AD于G、F.以D′D为直径作⊙O,设BD′的长为x,⊙O的面积为y.
(1)求y与x之间的函数关系式及自变量x的取值范围;
(2)连接EF,求EF与⊙O相切时x的值;
(3)设四边形ED′DF的面积为S,试求S关于x的函数表达式,并求x为何值时,S的值最大,最大值是多少?

查看答案和解析>>
科目:czsx
来源:第27章《二次函数》中考题集(39):27.3 实践与探索(解析版)
题型:解答题
如图(1),已知在△ABC中,AB=AC=10,AD为底边BC上的高,且AD=6.将△ACD沿箭头所示的方向平移,得到△A′CD′.如图(2),A′D′交AB于E,A′C分别交AB、AD于G、F.以D′D为直径作⊙O,设BD′的长为x,⊙O的面积为y.
(1)求y与x之间的函数关系式及自变量x的取值范围;
(2)连接EF,求EF与⊙O相切时x的值;
(3)设四边形ED′DF的面积为S,试求S关于x的函数表达式,并求x为何值时,S的值最大,最大值是多少?

查看答案和解析>>
科目:czsx
来源:2008年全国中考数学试题汇编《二次函数》(09)(解析版)
题型:解答题
(2008•滨州)如图(1),已知在△ABC中,AB=AC=10,AD为底边BC上的高,且AD=6.将△ACD沿箭头所示的方向平移,得到△A′CD′.如图(2),A′D′交AB于E,A′C分别交AB、AD于G、F.以D′D为直径作⊙O,设BD′的长为x,⊙O的面积为y.
(1)求y与x之间的函数关系式及自变量x的取值范围;
(2)连接EF,求EF与⊙O相切时x的值;
(3)设四边形ED′DF的面积为S,试求S关于x的函数表达式,并求x为何值时,S的值最大,最大值是多少?

查看答案和解析>>
科目:czsx
来源:2011-2012学年四川省泸州市泸县九中九年级(上)期中数学试卷(解析版)
题型:填空题
如图,已知∠ABC=∠ADE=90°,AC=AE,要证△ABC≌△ADE,需补充的条件是
.

查看答案和解析>>
科目:czsx
来源:第2章《二次函数》中考题集(39):2.3 二次函数的应用(解析版)
题型:解答题
如图(1),已知在△ABC中,AB=AC=10,AD为底边BC上的高,且AD=6.将△ACD沿箭头所示的方向平移,得到△A′CD′.如图(2),A′D′交AB于E,A′C分别交AB、AD于G、F.以D′D为直径作⊙O,设BD′的长为x,⊙O的面积为y.
(1)求y与x之间的函数关系式及自变量x的取值范围;
(2)连接EF,求EF与⊙O相切时x的值;
(3)设四边形ED′DF的面积为S,试求S关于x的函数表达式,并求x为何值时,S的值最大,最大值是多少?

查看答案和解析>>

 如图所示,已知∠CDA=∠AEB=90°,且CD=AE,AD=BE.问:
如图所示,已知∠CDA=∠AEB=90°,且CD=AE,AD=BE.问: (2013•威海)将一副直角三角板如图摆放,点C在EF上,AC经过点D.已知∠A=∠EDF=90°,AB=AC.∠E=30°,∠BCE=40°,则∠CDF=
(2013•威海)将一副直角三角板如图摆放,点C在EF上,AC经过点D.已知∠A=∠EDF=90°,AB=AC.∠E=30°,∠BCE=40°,则∠CDF=
 将一副直角三角板如图摆放,点C在EF上,AC经过点D.已知∠A=∠EDF=90°,AB=AC.∠E=30°,∠BCE=40°,则∠CDF=________.
将一副直角三角板如图摆放,点C在EF上,AC经过点D.已知∠A=∠EDF=90°,AB=AC.∠E=30°,∠BCE=40°,则∠CDF=________.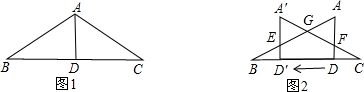


![]() 。如图(2),
。如图(2),![]() 交AB于E,
交AB于E,![]() 分别交AB.AD于G、F。以
分别交AB.AD于G、F。以![]() 为直径作⊙O,设
为直径作⊙O,设![]() 的长为x,⊙O的面积为y。
的长为x,⊙O的面积为y。![]() 的面积为S,试求S关于x的函数表达式,并求x为何值时,S的值最大,最大值是多少?
的面积为S,试求S关于x的函数表达式,并求x为何值时,S的值最大,最大值是多少?






