科目:czsx
来源:
题型:
已知,如图7所示,DE∥BC, BE平分∠ABC,且∠ABC=∠ACB,∠AED=72°,求 ∠CEB的度数.

查看答案和解析>>
科目:czsx
来源:
题型:
已知:如图15所示,CD⊥AB,BE⊥AC,垂足分别为D、E,BE、CD相交于点O,∠1=∠2,图中全等的三角形共有( )
 A.1对 B.2对 C.3对
A.1对 B.2对 C.3对  D.4对
D.4对

查看答案和解析>>
科目:czsx
来源:
题型:
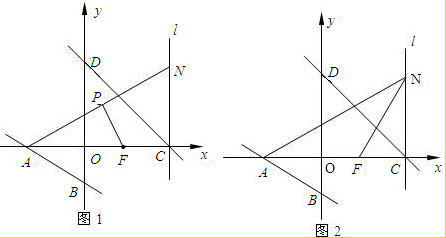
已知:如图1所示,直线x+y=9与x轴、y轴相交于C、D两点,直线2x+3y+12=0与x轴、y轴相交于A、B两点,F(4,0)是x轴上一点,过C点的直线l垂直于x轴,N是直线l上一点(N点与C点不重合),连接AN.
(1)求A、D两点的坐标;
(2)若P是AN的中点,PF=5,猜想∠APF的度数,并说明理由;
(3)如图2所示,连接NF,求△AFN外接圆面积的最小值,并求△AFN外接圆面积的最小时,圆心G的坐标.
查看答案和解析>>
科目:czsx
来源:
题型:
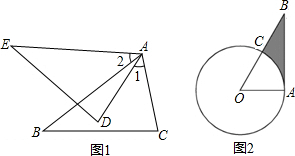
(2013•历城区二模)(1)已知:如图1所示,AB=AE,∠1=∠2,∠B=∠E.求证:BC=ED.
(2)如图2所示,AB是⊙O的切线,切点为A,OA=1,∠AOB=60°,求图中阴影部分的面积.
查看答案和解析>>
科目:czsx
来源:
题型:
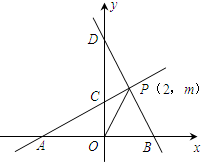
已知,如图1所示,直线PA与x轴交于点A,与y轴交于点C(0,2),且S
△AOC=4,直线BD与x轴交于点B,与y轴交于点D,直线PA与直线BD交于点P(2,m),点P在第一象限,连接OP.
(1)求点A的坐标;
(2)求直线PA的函数表达式;
(3)求m的值;
(4)若S
△BOP=S
△DOP,请你直接写出直线BD的函数表达式.
查看答案和解析>>
科目:czsx
来源:
题型:
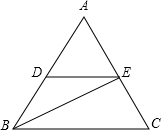
已知,如图所示,DE∥BC,BE平分∠ABC,且∠ABC=∠ACB,∠AED=72°,求∠CEB的度数.
查看答案和解析>>
科目:czsx
来源:
题型:
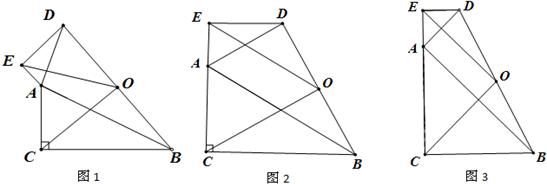
26、已知:如图1所示,Rt△ABC与Rt△ADE中,∠ACB=∠AED=90°,AC=kBC,AE=kDE,点O为线段BD的中点.探索∠COE、∠ADE之间有怎样的数量关系,证明你的结论.
说明:如果你反复探索没有解决问题,可以选取(1)和(2)中的条件,选(1)中的条件完成解答满分为7分;选(2)中的条件完成解答满分为4分.
(1)点E在CA延长线上(如图2);
(2)k=1,点E在CA延长线上(如图3).
查看答案和解析>>
科目:czsx
来源:2010年河北省石家庄市中考数学一模试卷(解析版)
题型:解答题
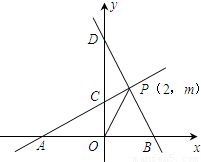
已知,如图1所示,直线PA与x轴交于点A,与y轴交于点C(0,2),且S
△AOC=4,直线BD与x轴交于点B,与y轴交于点D,直线PA与直线BD交于点P(2,m),点P在第一象限,连接OP.
(1)求点A的坐标;
(2)求直线PA的函数表达式;
(3)求m的值;
(4)若S
△BOP=S
△DOP,请你直接写出直线BD的函数表达式.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
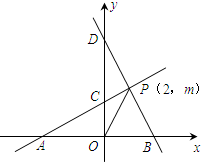 已知,如图1所示,直线PA与x轴交于点A,与y轴交于点C(0,2),且S△AOC=4,直线BD与x轴交于点B,与y轴交于点D,直线PA与直线BD交于点P(2,m),点P在第一象限,连接OP.
已知,如图1所示,直线PA与x轴交于点A,与y轴交于点C(0,2),且S△AOC=4,直线BD与x轴交于点B,与y轴交于点D,直线PA与直线BD交于点P(2,m),点P在第一象限,连接OP.
(1)求点A的坐标;
(2)求直线PA的函数表达式;
(3)求m的值;
(4)若S△BOP=S△DOP,请你直接写出直线BD的函数表达式.
查看答案和解析>>
科目:czsx
来源:2009年江苏省泰州市泰兴市四校联考试卷(解析版)
题型:解答题
(2009•泰兴市模拟)已知:如图1所示,直线x+y=9与x轴、y轴相交于C、D两点,直线2x+3y+12=0与x轴、y轴相交于A、B两点,F(4,0)是x轴上一点,过C点的直线l垂直于x轴,N是直线l上一点(N点与C点不重合),连接AN.
(1)求A、D两点的坐标;
(2)若P是AN的中点,PF=5,猜想∠APF的度数,并说明理由;
(3)如图2所示,连接NF,求△AFN外接圆面积的最小值,并求△AFN外接圆面积的最小时,圆心G的坐标.

查看答案和解析>>
科目:czsx
来源:2013年山东省济南市历城区中考数学二模试卷(解析版)
题型:解答题
(1)已知:如图1所示,AB=AE,∠1=∠2,∠B=∠E.求证:BC=ED.
(2)如图2所示,AB是⊙O的切线,切点为A,OA=1,∠AOB=60°,求图中阴影部分的面积.

查看答案和解析>>
科目:czsx
来源:
题型:解答题
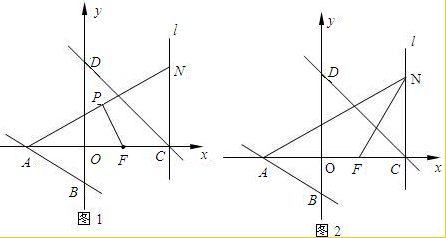
已知:如图1所示,直线x+y=9与x轴、y轴相交于C、D两点,直线2x+3y+12=0与x轴、y轴相交于A、B两点,F(4,0)是x轴上一点,过C点的直线l垂直于x轴,N是直线l上一点(N点与C点不重合),连接AN.
(1)求A、D两点的坐标;
(2)若P是AN的中点,PF=5,猜想∠APF的度数,并说明理由;
(3)如图2所示,连接NF,求△AFN外接圆面积的最小值,并求△AFN外接圆面积的最小时,圆心G的坐标.
查看答案和解析>>
科目:czsx
来源:新课标 读想练同步测试 七年级数学(下) 北师大版
题型:059
|
|
已知:如图甲所示,△ABC中,∠BAC=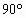 ,AB=AC,AE是过A点的一条直线,且B点和C点在AE的异侧,BD⊥AE于D点,CE⊥AE于E点.试说明: ,AB=AC,AE是过A点的一条直线,且B点和C点在AE的异侧,BD⊥AE于D点,CE⊥AE于E点.试说明:

| (1) |
|
(2) |
|
若直线AE绕点A旋转到如图乙所示的位置时(BD<CE),其余条件不变,问BD与DE、CE的关系如何?请予以证明;
|
|
(3) |
|
若直线AE绕点A旋转到如图丙所示的位置时(BD>CE),其余条件不变,BD与DE、CE的关系如何?直接写出结果,不需证明;
|
|
(4) |
|
归纳前三小题,用简捷的语言表述BD、DE、CE的关系.
|
|
|
查看答案和解析>>
科目:czsx
来源:
题型:047
(2005·四川成都)已知:如图a所示,△ABC是等边三角形,过AB边上的点D作DG∥BC,交AC于点G,在GD的延长线上取点E,使DE=DB,连接AE、CD.
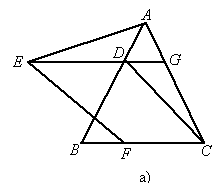
(1)求证:△AGE≌△DAC;
(2)过点E作EF∥DC,交BC于点F,请你连接AF,并判断△AEF是怎样的三角形,并证明你的结论.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
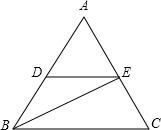 已知,如图所示,DE∥BC,BE平分∠ABC,且∠ABC=∠ACB,∠AED=72°,求∠CEB的度数.
已知,如图所示,DE∥BC,BE平分∠ABC,且∠ABC=∠ACB,∠AED=72°,求∠CEB的度数.
查看答案和解析>>
科目:czsx
来源:新教材 同步练 数学 七年级下册 配人教版
题型:044
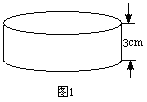
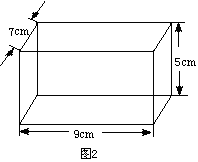
已知:如图1所示的圆柱形物体的底面积为9πcm2,若将其水平放入如图2所示的长方形盒子中,依据图中的数据,请你判断该圆柱形物体能放进盒子中吗?并说明理由.
查看答案和解析>>
科目:czsx
来源:2009年江苏省盐城市大丰市中考数学一模试卷(解析版)
题型:解答题
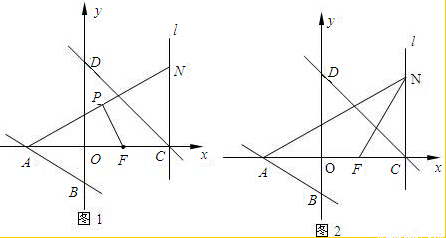
(2009•泰兴市模拟)已知:如图1所示,直线x+y=9与x轴、y轴相交于C、D两点,直线2x+3y+12=0与x轴、y轴相交于A、B两点,F(4,0)是x轴上一点,过C点的直线l垂直于x轴,N是直线l上一点(N点与C点不重合),连接AN.
(1)求A、D两点的坐标;
(2)若P是AN的中点,PF=5,猜想∠APF的度数,并说明理由;
(3)如图2所示,连接NF,求△AFN外接圆面积的最小值,并求△AFN外接圆面积的最小时,圆心G的坐标.
查看答案和解析>>
科目:czsx
来源:2011年辽宁省大连市中山区中考数学一模试卷(解析版)
题型:解答题
已知:如图1所示,Rt△ABC与Rt△ADE中,∠ACB=∠AED=90°,AC=kBC,AE=kDE,点O为线段BD的中点.探索∠COE、∠ADE之间有怎样的数量关系,证明你的结论.
说明:如果你反复探索没有解决问题,可以选取(1)和(2)中的条件,选(1)中的条件完成解答满分为7分;选(2)中的条件完成解答满分为4分.
(1)点E在CA延长线上(如图2);
(2)k=1,点E在CA延长线上(如图3).

查看答案和解析>>
科目:czsx
来源:
题型:解答题
已知:如图1所示,Rt△ABC与Rt△ADE中,∠ACB=∠AED=90°,AC=kBC,AE=kDE,点O为线段BD的中点.探索∠COE、∠ADE之间有怎样的数量关系,证明你的结论.
(1)点E在CA延长线上(如图2);
(2)k=1,点E在CA延长线上(如图3).
查看答案和解析>>
科目:czsx
来源:2012年江苏省无锡市蠡园中学中考适应性练习数学试卷(一)(解析版)
题型:解答题
已知:如图1所示,直线x+y=9与x轴、y轴相交于C、D两点,直线2x+3y+12=0与x轴、y轴相交于A、B两点,F(4,0)是x轴上一点,过C点的直线l垂直于x轴,N是直线l上一点(N点与C点不重合),连接AN.
(1)求A、D两点的坐标;
(2)若P是AN的中点,PF=5,猜想∠APF的度数,并说明理由;
(3)如图2所示,连接NF,求△AFN外接圆面积的最小值,并求△AFN外接圆面积的最小时,圆心G的坐标.

查看答案和解析>>

![]() A.1对 B.2对 C.3对
A.1对 B.2对 C.3对 ![]() D.4对
D.4对


 已知,如图1所示,直线PA与x轴交于点A,与y轴交于点C(0,2),且S△AOC=4,直线BD与x轴交于点B,与y轴交于点D,直线PA与直线BD交于点P(2,m),点P在第一象限,连接OP.
已知,如图1所示,直线PA与x轴交于点A,与y轴交于点C(0,2),且S△AOC=4,直线BD与x轴交于点B,与y轴交于点D,直线PA与直线BD交于点P(2,m),点P在第一象限,连接OP.

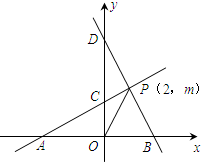 已知,如图1所示,直线PA与x轴交于点A,与y轴交于点C(0,2),且S△AOC=4,直线BD与x轴交于点B,与y轴交于点D,直线PA与直线BD交于点P(2,m),点P在第一象限,连接OP.
已知,如图1所示,直线PA与x轴交于点A,与y轴交于点C(0,2),且S△AOC=4,直线BD与x轴交于点B,与y轴交于点D,直线PA与直线BD交于点P(2,m),点P在第一象限,连接OP.








