
科目:czsx 来源: 题型:
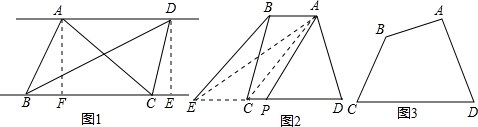
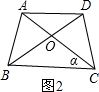
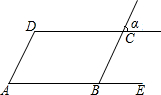 如图,若AD∥BC,∠A=∠α,则AB∥CD,说出说理过程.
如图,若AD∥BC,∠A=∠α,则AB∥CD,说出说理过程.科目:czsx 来源: 题型:
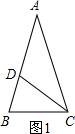
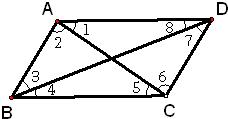 16、如图,若AD∥BC,则
16、如图,若AD∥BC,则科目:czsx 来源: 题型:
科目:czsx 来源: 题型:阅读理解
| 1 |
| 2 |
| 1 |
| 2 |
科目:czsx 来源: 题型:
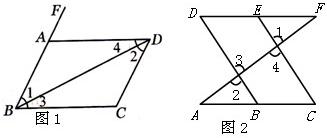 18、补全下列各题解题过程.
18、补全下列各题解题过程.科目:czsx 来源: 题型:
科目:czsx 来源: 题型:
| 1 | ||||
|
| 5 |
| 10 |
| 1 |
| 2 |
| 3 |
| 6 |
| 1 |
| 3 |
| 3 |
科目:czsx 来源: 题型:
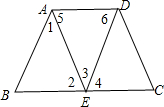
 已知点D是等边△ABC的边BC上一点,以AD为边向右作等边△ADF,DF、AC交于点N.
已知点D是等边△ABC的边BC上一点,以AD为边向右作等边△ADF,DF、AC交于点N.科目:czsx 来源: 题型:
 解答题
解答题 科目:czsx 来源: 题型:
科目:czsx 来源: 题型:
| CB |
| AC |
| AC |
| AB |
| ||
| 2 |
科目:czsx 来源: 题型:
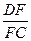 的值.
的值. 科目:czsx 来源:2011届北京市门头沟区初三第一学期期末数学卷 题型:解答题
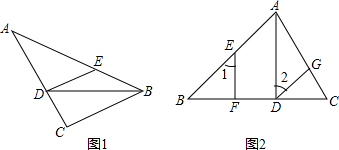
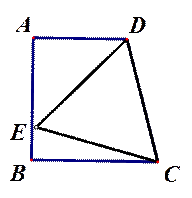
如图1,AD∥BC,AB ⊥BC于B,∠DCB=75°,以CD为边的等边△DCE的另一顶点E在线段AB上.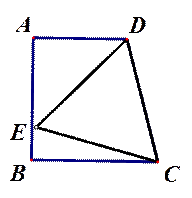
(1)填空:∠ADE=____°;
(2)求证: AB=BC;
(3)如图2所示,若F为线段CD上一点,∠FBC=30°,求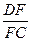 的值.
的值.
科目:czsx 来源:2011-2012学年重庆万州区岩口复兴学校九年级下第一次月考数学试卷(解析版) 题型:解答题
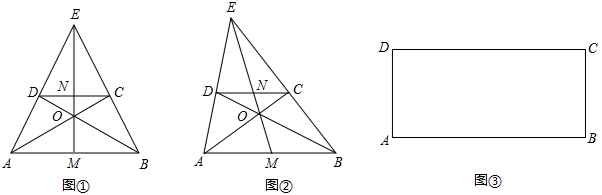
尺规作图:学校决定在植物园内开辟一块梯形土地ABCD培植草皮(如图),AD∥BC.其中MN是园林里的一条主水管,点B、点C在MN上.如今要在BC上的P点接一条与BC垂直的水管 ,并在这条新接水管的某处安置喷淋器E,喷淋器位于草坪内,且到AB、BC的距离相等.请你运用尺规作图,在原图中帮助确定点E的位置.(要求:不写已知、求作及作法;保留作图痕迹)

科目:czsx 来源:2010-2011学年北京市门头沟区初三第一学期期末数学卷 题型:解答题
如图1,AD∥BC,AB ⊥BC于B,∠DCB=75°,以CD为边的等边△DCE的另一顶点E在线段AB上.
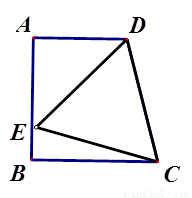
(1)填空:∠ADE=____°;
(2)求证: AB=BC;
(3)如图2所示,若F为线段CD上一点,∠FBC=30°,求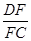 的值.
的值.
科目:czsx 来源:浙教版初一数学认识时间的可能性专项训练 题型:填空题
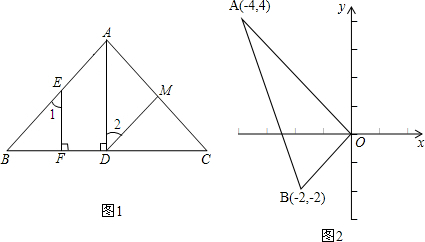
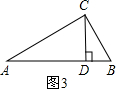
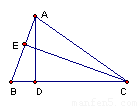
.如图,△ABC中,AD⊥BC于D,CE⊥AB于E,且BE=2AE,已知AD=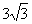 , tan∠BCE=
, tan∠BCE=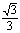 ,那么CE=
,那么CE=
科目:czsx 来源: 题型:
如图1,AD∥BC,AB ⊥BC于B,∠DCB=75°,以CD为边的等边△DCE的另一顶点E在线段AB上.
(1)填空:∠ADE=____°;
(2)求证: AB=BC;
(3)如图2所示,若F为线段CD上一点,∠FBC=30°,求的值.