请直接写出S=|x-1|+|x-2|+...|x-99|的值答案解析

科目：czsx 来源： 题型：

24、某校为了解九年级男生1000米长跑的成绩，从中随机抽取了50名男生进行测试，根据测试评分标准，将他们的得分进行统计后分为A、B、C、D四等，并绘制成下面的频数分布表和扇形统计图：

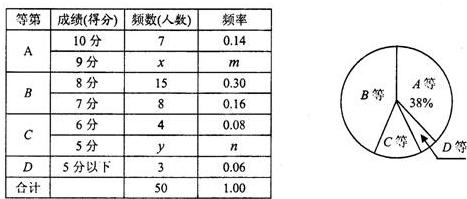
（1）请直接写出x，y，m，n的值：x=

12

，y=

1

，m=

0.24

，n=

0.02

；
（2）求出表示得分为C等的扇形的圆心角的度数．

科目：czsx 来源：江苏期末题 题型：解答题

某校为了解九年级男生1000米长跑的成绩，从中随机抽取了50名男生进行测试，根据测试评分标准，将他们的得分进行统计后分为A、B、C、D四等，并绘制成下面的频数分布表和扇形统计图：

（1）请直接写出x，y，m，n的值：x=____，y=____，m=____，n=____；
（2）求出表示得分为C等的扇形的圆心角的度数。

科目：czsx 来源：江苏省期末题 题型：解答题

某校为了解九年级男生1000米长跑的成绩，从中随机抽取了50名男生进行测试，根据测试评分标准，将他们的得分进行统计后分为A、B、C、D四等，并绘制成下面的频数分布表和扇形统计图：

（1）请直接写出x，y，m，n的值：x=（    ），y=（    ），m=（    ），n=（    ）；
（2）求出表示得分为C等的扇形的圆心角的度数。

科目：czsx 来源： 题型：

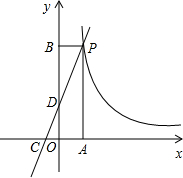
如图，一次函数y=kx+2的图象与反比例函数y=

m

x

的图象交于点P，点P在第一象限，PA⊥x轴于点A，PB⊥y轴于点B．一次函数的图象分别交x轴、y轴于点C、D，且S_△PBD=4，

OC

OA

=

1

2

．
（1）求点D的坐标及BD长；
（2）求一次函数与反比例函数的解析式；
（3）根据图象直接写出当x＞0时，一次函数的值大于反比例函数值的x的取值范围；
（4）若双曲线上存在一点Q，使以B、D、P、Q为顶点的四边形是直角梯形，请直接写出符合条件的Q点的坐标．

科目：czsx 来源： 题型：

如图，一次函数y=kx+b的图象与反比例函数y=

m

x

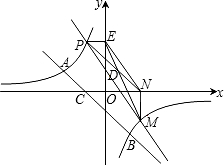
的图象相交于点A（-2，1）、点B（1，n）．
（1）求此一次函数和反比例函数的解析式；
（2）请直接写出满足不等式kx+b-

m

x

＞0的解集；
（3）若点P是双曲线左支上一动点，过点P的直线与双曲线另一支交于点M，过点P作PE⊥y轴，过点M作MN⊥x轴，垂足分别为E、N，PN与ME交于点D，请判断△PDE与△MDN面积的大小关系，并说明理由．

科目：czsx 来源： 题型：

图1，线段AB、CD相交于点O，连接AD、CB，我们把形如图1的图形称之为“8字形”．如图2，在图1的条件下，∠DAB和∠BCD的平分线AP和CP相交于点P，并且与CD、AB分别相交于M、N．试解答下列问题：
（1）在图1中，请直接写出∠A、∠B、∠C、∠D之间的数量关系：

∠A+∠D=∠C+∠B

∠A+∠D=∠C+∠B

；
（2）仔细观察，在图2中“8字形”的个数：

6

6

个；
（3）图2中，当∠D=50度，∠B=40度时，求∠P的度数．

科目：czsx 来源： 题型：

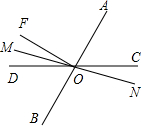
如图，直线AB、CD、MN相交于O，∠DOB=60°，BO⊥FO，OM平分∠DOF．
（1）求∠MOF的度数；
（2）求∠AON的度数；
（3）请直接写出图中所有与∠AON互余的角．

科目：czsx 来源： 题型：

科目：czsx 来源： 题型：

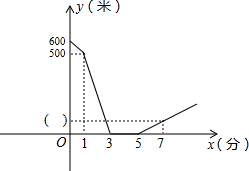
（2013•海门市二模）五一假期中，小明和小亮相约晨练跑步．小明比小亮早1分钟离开家门，3分钟后迎面遇到从家跑来的小亮．两人沿滨江路并行跑了2分钟后，决定进行直线长跑比赛，比赛时小明的速度始终是250米/分，小亮的速度始终是300米/分．下图是两人之间的距离y（米）与小明离开家的时间x（分钟）之间的函数图象，根据图象回答下列问题：
（1）请直接写出小明和小亮比赛前的速度，并说出图中点A（1，500）的实际意义；
（2）请在图中的

100

100

内填上正确的值，并求两人比赛过程中y与x之间的函数关系式；
（3）若小亮从家出门跑了11分钟时，立即按原路以比赛时的速度返回，则小亮再经过多少分钟时两人相距75米？

科目：czsx 来源： 题型：

已知四边形OABC是边长为4的正方形，分别以OA、OC所在的直线为x轴、y轴，建立如图1所示的平面直角坐标系，直线l经过A、C两点．
（1）求直线l的函数表达式；
（2）若P是直线l上的一个动点，请直接写出当△OPA是等腰三角形时点P的坐标；
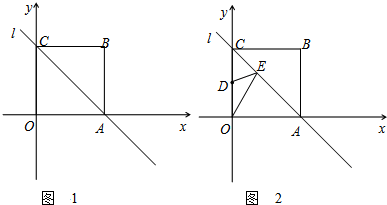
（3）如图2，若点D是OC的中点，E是直线l上的一个动点，求使OE+DE取得最小值时点E的坐标．

科目：czsx 来源： 题型：

25、图1，线段AB、CD相交于点O，连接AD、CB，我们把形如图1的图形称之为“8字形”．如图2，在图1的条件下，∠DAB和∠BCD的平分线AP和CP相交于点P，并且与CD、AB分别相交于M、N．试解答下列问题：
（1）在图1中，请直接写出∠A、∠B、∠C、∠D之间的数量关系：

∠A+∠D=∠C+∠B

；
（2）仔细观察，在图2中“8字形”的个数：

3

个；
（3）图2中，当∠D=50度，∠B=40度时，求∠P的度数．
（4）图2中∠D和∠B为任意角时，其他条件不变，试问∠P与∠D、∠B之间存在着怎样的数量关系．说明理由．（直接写出结果，不必证明）．

科目：czsx 来源： 题型：

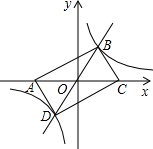
如图，在平面直角坐标系中，正比例函数y=kx（k≠0）的图象与反比例函数y=

3

x

的图象分别交于第一、三象限的点B、D，已知点A（-m，0）、C（m，0）．连接AB、BC、CD、DA．
（1）四边形ABCD的形状一定是

 

．
（2）若m=2且四边形ABCD是矩形，求点B的坐标．
（3）试探究：当直线y=kx绕原点O旋转时，四边形ABCD能不能是菱形？若能，请直接写出A、B、C、D的坐标；若不能，请说明理由．

科目：czsx 来源： 题型：

如图1，在△ABC中，∠ACB=90°，AC=BC，直线MN经过点C，且AD⊥MN于D，BE⊥MN于E．易得DE=AD+BE（不需证明）．
（1）若直线CE绕C点旋转到图2的位置时，其余条件不变，你认为上述结论是否成立？若成立，写出证明过程；若不成立，请写出此时DE、AD、BE之间的数量关系，并说明理由；
（2）若直线CE绕C点旋转到图3的位置时，其余条件不变，请直接写出此时DE、AD、BE之间的数量关系（不需证明）．

科目：czsx 来源： 题型：

如图，在Rt△ABC中，∠ABC=90°，AB=8，BC=6，点D为AC边上的动点，点D从点C出发，沿边CA往A运动，当运动到点A时停止，若设点D运动的时间为t秒，点D运动的速度为每秒1个单位长度
（1）当t=2时，CD=

2

2

，AD=

8

8

；（请直接写出答案）
（2）当△CBD是直角三角形时，t=

3.6或10秒

3.6或10秒

；（请直接写出答案）
（3）求当t为何值时，△CBD是等腰三角形？并说明理由．

科目：czsx 来源： 题型：

如图，A、B、C为一个平行四边形的三个顶点，且A、B、C三点的坐标分别为（3，3）、（6，4）、（4，6）
（1）请直接写出这个平行四边形第四个顶点的坐标；
（2）在△ABC中，试求出AB边上的高．

科目：czsx 来源： 题型：

已知：如图1，线段AB、CD相交于点O，连接AD、CB，我们把形如图1的图形称之为“8字形”．试解答下列问题：
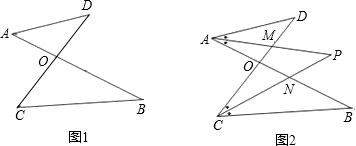
（1）在图1中，请直接写出∠A、∠B、∠C、∠D之间的数量关

∠A+∠D=∠B+∠C

∠A+∠D=∠B+∠C

；
（2）仔细观察，在图2中“8字形”的个数：

6

6

个；
（3）在图2中，若∠D=40°，∠B=36°，∠DAB和∠BCD的平分线AP和CP相交于点P，并且与CD、AB分别相交于M、N．利用（1）的结论，试求∠P的度数；
（4）如果图2中∠D和∠B为任意角时，其他条件不变，试问∠P与∠D、∠B之间存在着怎样的数量关系．（直接写出结论即可）

科目：czsx 来源： 题型：

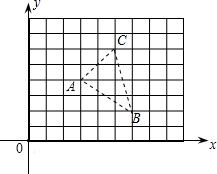
如图，A、B、C为一个平行四边形的三个顶点，且A、B、C三点的坐标分别为（3，4）、（6，2）、（5，6）．
（1）请直接写出这个平行四边形第四个顶点的坐标；
（2）求此平行四边形的周长．

科目：czsx 来源： 题型：

已知如图1，线段AB、CD相交于点O，连接AD、CB，我们把形如图1的图形称之为“8字形”．如图2，在图1的条件下，∠DAB和∠BCD的平分线AP和CP相交于点P，并且与CD、AB分别相交于M、N．试解答下列问题：

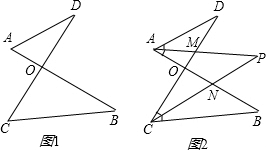
（1）在图1中，请直接写出∠A、∠B、∠C、∠D之间的数量关系：

 

；
（2）仔细观察，在图2中“8字形”的个数：

 

个；
（3）在图2中，若∠D=40°，∠B=36°，试求∠P的度数；
（4）如果图2中∠D和∠B为任意角时，其他条件不变，试问∠P与∠D、∠B之间存在着怎样的数量关系．（直接写出结论即可）

科目：czsx 来源： 题型：

28、已知：如图1，线段AB、CD相交于点O，连接AD、CB、如图2，在图1的条件下，∠DAB和∠BCD的平分线AP和CP相交于点P，并且与CD、AB分别相交于M、N．试解答下列问题：
（1）在图1中，请直接写出∠A、∠B、∠C、∠D之间的数量关系：

∠A+∠D=∠B+∠C

；
（2）在图2中，若∠D=40°，∠B=30°，试求∠P的度数；（写出解答过程）
（3）如果图2中∠D和∠B为任意角，其他条件不变，试写出∠P与∠D、∠B之间数量关系．（直接写出结论即可）

科目：czsx 来源： 题型：

如图，把一张标准纸一次又一次对开，得到“2开”纸，“4开”纸，“8开”纸，“16开”纸…．已知标准纸的短边长为a．
（1）如图2，把这张标准纸对开得到的“16开”张纸按如下步骤折叠：
第一步：将矩形的短边AB与长边AD对齐折叠，点B落在AD上的点B'处，铺平后得折痕AE；
第二步：将长边AD与折痕AE对齐折叠，点D正好与点E重合，铺平后得折痕AF．
则AD：AB的值是

 

，AD，AB的长分别是

 

，

 

；
（2）“2开”纸，“4开”纸，“8开”纸的长与宽之比是否都相等？若相等，直接写出这个比值；若不相等，请分别计算它们的比值；
（3）如图3，由8个大小相等的小正方形构成“L”型图案，它的四个顶点E，F，G，H分别在“16开”纸的边AB，BC，CD，DA上，求DG的长；
（4）已知梯形MNPQ中，MN∥PQ，∠M=90°，MN=MQ=2PQ，且四个顶点M，N，P，Q都在“4开”纸的边上，请直接写出2个符合条件且大小不同的直角梯形的面积．