
科目:czsx 来源: 题型:
 如图下列条件
如图下列条件科目:czsx 来源: 题型:
| BD |
| CD |
| 1 |
| 2 |
| AE |
| AF |
| BD |
| CD |
| m |
| n |
| AE |
| AF |
科目:czsx 来源:69领航·单元同步训练 八年级(上册) 数学(人教版) 题型:022
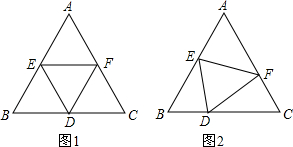
如图,BA⊥AC,CD∥AB,AB=CE,∠ABC=∠DEC,则△CDE≌________,理由是________;且有∠ACB=________,∠ABC=________,故BC与DE互相垂直.

科目:czsx 来源: 题型:
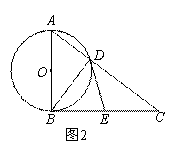
已知Rt△ABC中,∠ABC=90°,以AB为直径作⊙O交AC于点D,连结BD.
(1)如图1,若BD∶CD=3∶4,AD=3,求⊙O的直径 AB的长;
(2)如图2,若E是BC的中点,连结ED![]() ,请你判断直线ED与⊙O的位置关系,并证明你的结论
,请你判断直线ED与⊙O的位置关系,并证明你的结论
 .
.
科目:czsx 来源:同步题 题型:填空题

科目:czsx 来源: 题型:单选题
 如图下列条件
如图下列条件科目:czsx 来源: 题型:
| PE |
| PB |
| 1 |
| 2 |
| 1 |
| 2 |

科目:czsx 来源: 题型:
科目:czsx 来源: 题型:

科目:czsx 来源: 题型:
科目:czsx 来源: 题型:
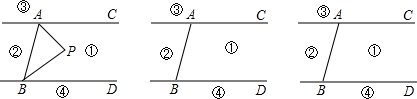
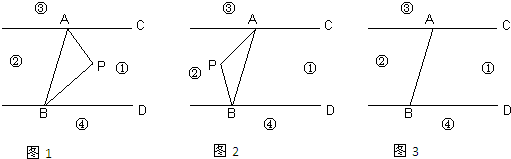
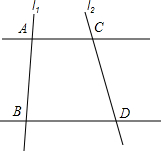 如图,直线AC∥BD,直线l1、l2分别交AC、BD于点A、C、B、D,点P在直线l2上(异于C、D两点).设∠PAC=α、∠PBD=β、∠APB=γ.
如图,直线AC∥BD,直线l1、l2分别交AC、BD于点A、C、B、D,点P在直线l2上(异于C、D两点).设∠PAC=α、∠PBD=β、∠APB=γ.