精英家教网 >
试题搜索列表 >第一象限内的点p(x,y)为直线y=-2x+4上的一个动点,pa垂直x轴,pb垂直y轴,垂直分别是a,b
第一象限内的点p(x,y)为直线y=-2x+4上的一个动点,pa垂直x轴,pb垂直y轴,垂直分别是a,b答案解析
科目:czsx
来源:
题型:
双曲线y=
上一点P,过P作x轴,y轴的垂线,垂足分别为A、B,矩形OAPB的面积为2,则双曲线与直线在y=kx-4交点在第一象限内的点的坐标为
.
查看答案和解析>>
科目:czsx
来源:
题型:

两个反比例函数
y=,
y=在第一象限内的图象如图所示,点P
1、P
2在反比例函数图象上,过点P
1作x轴的平行线与过点P
2作y轴的平行线相交于点N,若点N(m,n)恰好在
y=的图象上,则NP
1与NP
2的乘积是
3
3
.
查看答案和解析>>
科目:czsx
来源:
题型:
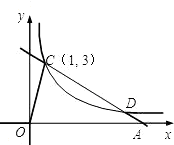
如图,反比例函数
y=图象在第一象限的分支上有一点C(1,3),过点C的直线y=k
2x+b(k
2<0,b为常数)与x轴交于点A(a,0).
(1)求反比例函数的解析式;
(2)求A点横坐标a和k
2之间的函数关系式;
(3)当直线与反比例函数的图象在第一象限内的另一交点的横坐标为3时,求△COA的面积.
查看答案和解析>>
科目:czsx
来源:
题型:

如图,在平面直角坐标系中,已知A(0,4)、B(2,0),在第一象限内的点C,使△ABC为等腰直角三角形,则点C的坐标为
(6,2)或(4,6)或(3,3)
(6,2)或(4,6)或(3,3)
.
查看答案和解析>>
科目:czsx
来源:
题型:
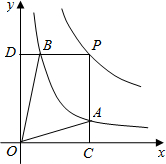
(2013•眉山模拟)函数y=
和y=
在第一象限内的图象如图,点P是y=
的图象上一动点,PC⊥x轴于点C,交y=
的图象于点B.给出如下结论:①△ODB与△OCA的面积相等;②PA与PB始终相等;③四边形PAOB的面积大小不会发生变化;④CA=
AP.其中所有正确结论的序号是( )
查看答案和解析>>
科目:czsx
来源:
题型:

反比例函数
y=(k>0)在第一象限内的图象如图,点M是图象上一点,MP垂直x轴于点P,如果△MOP的面积为8,那么k的值等于
.
查看答案和解析>>
科目:czsx
来源:
题型:
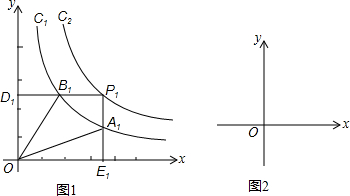
如图,两个反比例函数
y1=和
y2=在第一象限内的图象依次是C
1和C
2,设点p
1在c
2上,p
1E
1⊥x轴于点E
1,p
1D
1⊥y轴与点D
1,交C
1于点A
1交c
1与点B
1.
(1)求出四边形P
1A
1OB
1的面积S
1;
(2)若
y3=在第一象限的图象是c
3,p
2是C
3上的点,P
2E
2⊥x轴于点E
2,交C
2于点A
2,P
2D
2⊥y轴于点D
2,交C
2于点B
2,则四边形P
2A
2OB
2的面积S
2=
1
1
.
(3)按此类推,试猜想四边形P
nA
nOB
n的面积S
n=
1
1
,在所给坐标系中画出草图,并验证你的猜想.
查看答案和解析>>
科目:czsx
来源:
题型:

(2013•莆田模拟)函数y=
和y=
在第一象限内的图象如图,点P是y=
的图象上一动点,PC⊥x轴于C,交y=
的图象于点A,PD⊥y轴于D,交y=
的图象于点B.
给出如下结论:①△ODB与△OCA的面积相等;②PA与PB始终相等;③四边形PAOB的面积大小不会发生变化;④
=.
其中所有正确结论的序号是
①③④
①③④
.
查看答案和解析>>
科目:czsx
来源:
题型:
(2011•宁德)直线y=x-6与x轴、y轴分别交于点A、B,点E从B点,出发以每秒1个单位的速度沿线段BO向O点移动(与B、O点不重合),过E作EF∥AB,交x轴于F.将四边形ABEF沿EF折叠,得到四边形DCEF,设点E的运动时间为t秒.
(1)①直线y=x-6与坐标轴交点坐标是A(
6
6
,
0
0
),B(
0
0
,
-6
-6
);
②画出t=2时,四边形ABEF沿EF折叠后的图形(不写画法);
(2)若CD交y轴于H点,求证:四边形DHEF为平行四边形;并求t为何值时,四边形DHEF为菱形(计算结果不需化简);
(3)设四边形DCEF落在第一象限内的图形面积为S,求S关于t的函数
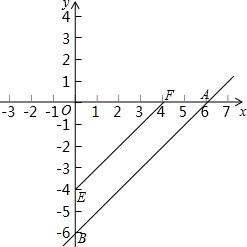
表达式,并求出S的最大值.
查看答案和解析>>
科目:czsx
来源:
题型:
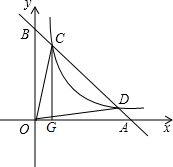
如图,已知C、D是双曲线
y=在第一象限内的分支上的两点,直线CD分别交x轴,y轴于A、B两点,过点C作CG⊥x轴于点G,设C、D的坐标分别为(x
1,y
1),(x
2,y
2),连结OC、OD.
(1)求证:
y1<OC<y1+;
(2)若
OC=,==,求直线CD的解析式.
查看答案和解析>>
科目:czsx
来源:
题型:
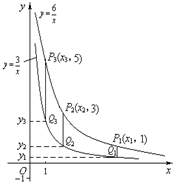
两个反比例函数
y=,
y=在第一象限内的图象如图所示,点P
1,P
2,P
3,…,P
2009在反比例函数
y=图象上,它们的横坐标分别是x
1,x
2,x
3,…,x
2009,纵坐标分别是1,3,5,…,共2009个连续奇数,过点P
1,P
2,P
3,…,P
2009分别作y轴的平行线,与
y=的图象交点依次是Q
1(x
1,y
1),Q
2(x
2,y
2),Q
3(x
3,y
3),…,Q
2009(x
2009,y
2009),则y
2009=
.
查看答案和解析>>
科目:czsx
来源:
题型:
如图1,已知直线y=kx与抛物线
y=-x2+交于点A(3,6).
(1)求k的值;
(2)点P为抛物线第一象限内的动点,过点P作直线PM,交x轴于点M(点M、O不重合),交直线OA于点Q,再过点Q作直线PM的垂线,交y轴于点N.试探究:线段QM与线段QN的长度之比是否为定值?如果是,求出这个定值;如果不是,说明理由;
(3)如图2,若点B为抛物线上对称轴右侧的点,点E在线段OA上(与点O、A不重合),点D(m,0)是x轴正半轴上的动点,且满足∠BAE=∠BED=∠AOD.继续探究:m在什么范围时,符合条件的E点的个数分别是1个、2个?
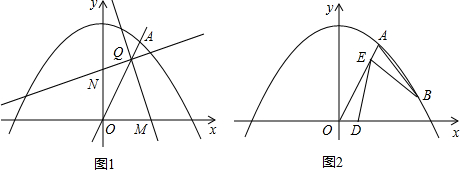
查看答案和解析>>
科目:czsx
来源:
题型:
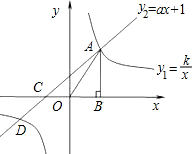
如图,已知反比例函数
y1=和一次函数y
2=ax+1的图象相交于第一象限内的点A,且点A的横坐标为1.过点A作AB⊥x轴于点B,△AOB的面积为1.
(1)求反比例函数和一次函数的解析式;
(2)若一次函数y
2=ax+1的图象与x轴相交于点C,求∠ACO的度数;
(3)结合图象直接写出:当y
1>y
2>0时,x的取值范围.
查看答案和解析>>
科目:czsx
来源:
题型:
已知P(x1,y1)、Q(x2,y2)是直角坐标系第一象限内的点,给出下列说法:①P、Q必定在同一抛物线上;②P、Q必定在同一双曲线上;③P、Q必定在同一直线上.其中正确的个数是( )
查看答案和解析>>
科目:czsx
来源:
题型:
如图,在平面直角坐标系中,点P(x,y)是直线y=-x+8上在第一象限内的点,点A(6,0),O
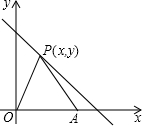
是坐标原点,△PAO的面积为S.
(1)求S与x的函数关系式,并写出x的取值范围,画出S关于x的函数图象;
(2)当P点运动到什么位置时△PAO的面积为15;
(3)当P点运动到什么位置时,点P到两坐标轴的距离相等.
查看答案和解析>>
科目:czsx
来源:
题型:
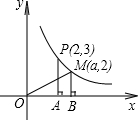
如图,在第一象限内,点P,M(a,2)是双曲线
y=(k≠0)上的两点,PA⊥x轴于点A,MB⊥x轴于点B,PA与OM交于点C,则△OAC的面积为
.
查看答案和解析>>
科目:czsx
来源:
题型:

如图,⊙C经过原点且与两坐标轴分别交于点A(0,2)和点B,D为⊙C在第一象限内的一点,且∠ODB=60°,求⊙C的半径、线段AB的长、B点坐标及圆心C的坐标.
查看答案和解析>>
科目:czsx
来源:
题型:

如图,一次函数y=k
1x+b的图象经过A(0,-2),B(1,0)两点,与反比例函数
y=的图象在第一象限内的交点为M,若△OBM的面积为2.
(1)求一次函数和反比例函数的表达式;
(2)在x轴上是否存在点P,使AM⊥MP?若存在,求出点P的坐标;若不存在,说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
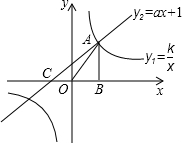
如图,已知反比例函数
y1=和一次函数y
2=ax+1的图象相交于第一象限内的点A,且点A的横坐标为1.过点A作AB⊥x轴于点B,△AOB的面积为1.
(1)求反比例函数和一次函数的解析式.
(2)若一次函数的图象与x轴相交于点C,求线段AC的长度.
(3)直接写出:当y
1>y
2>0时,x的取值范围.
(4)在y轴上是否存在一点P,使△PAO为等腰三角形?若存在,请直接写出p点坐标;若不存在,请说明理由.(要求至少写两个)
查看答案和解析>>
科目:czsx
来源:
题型:
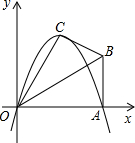
(2012•定西)在Rt△OAB中,∠OAB=90°,∠BOA=30°,AB=2,若以O为坐标原点,OA所在直线为x轴,建立如图所示的平面之间坐标系,点B在第一象限内,将Rt△OAB沿OB折叠后,点A落在第一象限内的点C处.
(1)点C的坐标为
;
(2)若抛物线y=ax
2+bx经过C,A两点,求此抛物线的解析式;
(3)若抛物线的对称轴与OB交于点D,点P为线段DB上一点,过P作y轴的平行线,交抛物线于点M,问:是否存在这样的点P,使得四边形CDPM为等腰梯形?若存在,求出此时点P的坐标,若不存在,请说明理由.
查看答案和解析>>

 两个反比例函数y=
两个反比例函数y= 如图,反比例函数y=
如图,反比例函数y= 如图,在平面直角坐标系中,已知A(0,4)、B(2,0),在第一象限内的点C,使△ABC为等腰直角三角形,则点C的坐标为
如图,在平面直角坐标系中,已知A(0,4)、B(2,0),在第一象限内的点C,使△ABC为等腰直角三角形,则点C的坐标为 (2013•眉山模拟)函数y=
(2013•眉山模拟)函数y=
 (2013•莆田模拟)函数y=
(2013•莆田模拟)函数y=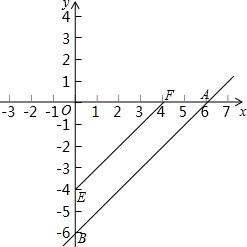 表达式,并求出S的最大值.
表达式,并求出S的最大值. 如图,已知C、D是双曲线y=
如图,已知C、D是双曲线y= 两个反比例函数y=
两个反比例函数y=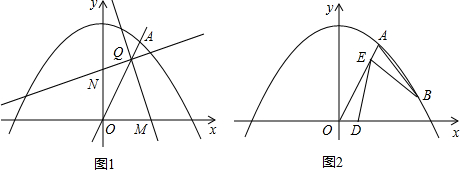
 如图,已知反比例函数y1=
如图,已知反比例函数y1= 是坐标原点,△PAO的面积为S.
是坐标原点,△PAO的面积为S. 如图,在第一象限内,点P,M(a,2)是双曲线y=
如图,在第一象限内,点P,M(a,2)是双曲线y= 如图,⊙C经过原点且与两坐标轴分别交于点A(0,2)和点B,D为⊙C在第一象限内的一点,且∠ODB=60°,求⊙C的半径、线段AB的长、B点坐标及圆心C的坐标.
如图,⊙C经过原点且与两坐标轴分别交于点A(0,2)和点B,D为⊙C在第一象限内的一点,且∠ODB=60°,求⊙C的半径、线段AB的长、B点坐标及圆心C的坐标. 如图,一次函数y=k1x+b的图象经过A(0,-2),B(1,0)两点,与反比例函数y=
如图,一次函数y=k1x+b的图象经过A(0,-2),B(1,0)两点,与反比例函数y= 如图,已知反比例函数y1=
如图,已知反比例函数y1= (2012•定西)在Rt△OAB中,∠OAB=90°,∠BOA=30°,AB=2,若以O为坐标原点,OA所在直线为x轴,建立如图所示的平面之间坐标系,点B在第一象限内,将Rt△OAB沿OB折叠后,点A落在第一象限内的点C处.
(2012•定西)在Rt△OAB中,∠OAB=90°,∠BOA=30°,AB=2,若以O为坐标原点,OA所在直线为x轴,建立如图所示的平面之间坐标系,点B在第一象限内,将Rt△OAB沿OB折叠后,点A落在第一象限内的点C处.