精英家教网 >
试题搜索列表 >如图,已知在△ABC中,角A=40°角B=75°,图中各三角形与△ABC相似的是
如图,已知在△ABC中,角A=40°角B=75°,图中各三角形与△ABC相似的是答案解析
科目:czsx
来源:
题型:
26、
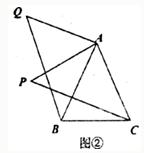
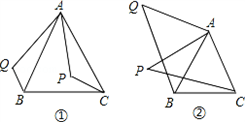
复习“全等三角形”的知识时,老师布置了一道作业题:“如下图①,已知在△ABC中,AB=AC,P是△ABC内部任意一点,将AP绕A顺时针旋转至AQ,使得∠QAP=∠BAC,连接BQ、CP,则BQ=CP.”
(1)小亮是个爱动脑筋的同学,他通过对图①的分析,证明了△ABQ≌△ACP,从而证得BQ=CP.请你帮小亮完成证明.
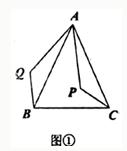
(2)之后,小亮又将点P移到等腰三角形ABC之外,原题中的条件不变,“BQ=CP”仍然成立吗?若成立,请你就图②给出证明.若不成立,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
复习“全等三角形”的知识时,老师布置了一道作业题:“如下图①,已知在△ABC中,AB=AC,P是△ABC内部任意一点,将AP绕A顺时针旋转至AQ,使得∠QAP=∠BAC,连接BQ、CP,则BQ=CP。”

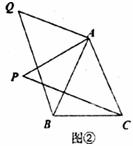
(1)小亮是个爱动脑筋的同学,他通过对图①的分析,证明了△ABQ≌△ACP,从而证得BQ=CP。请你帮小亮完成证明。
(2)之后,小亮又将点P移到等腰三角形ABC之外,原题中的条件不变,“BQ=CP”仍然成立吗?若成立,请你就图②给出证明。若不成立,请说明理由。
查看答案和解析>>
科目:czsx
来源:数学教研室
题型:044
请阅读下列材料,并回答所提出的问题。
三角形内角平分线性质定理:三角形的内角平分线分对边所得的线段与两
边对应成比例。
已知:如图,在△ABC中,AD是角平分线。
求证: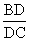 =
=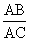 。
。

分析:要证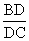 =
= ,一般只要证BD、DC与AB、AC
,一般只要证BD、DC与AB、AC
或BD、AB与DC、AC所在的三角形相似即可,现在点B、D、C
在一条直线上,△ABD与△ADC不相似,需要考虑用别的方法换比。在比例式
= 中,AC恰是BD、DC、AB的第四比例项,所以考虑过点C作CE//AD,交
中,AC恰是BD、DC、AB的第四比例项,所以考虑过点C作CE//AD,交
BA的延长线于点E,从而得到BD、DC、AB的第四比例项AE,这样,证明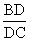 =
=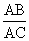
就可以转化成证AE=AC。
证明:过点C作CE//DA交BA的延长线于点E。
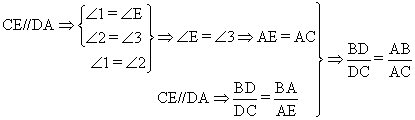 。
。
(1)在上述证明过程中,用到了哪些定理?(写对两个定理即可)
(2)在上述分析、证明过程中,主要利用到了下列三种数学思想中的哪一种?选出一
个填在后面的括号内………………………………………………………………( )
A. 数形结合思想
B. 转化思想
C. 分类讨论思想
(3)用三角形内角平分线性质定理解答问题。
如下图,已知在△ABC中,AD是角平分线,AB=5cm,AC=4cm,
BC=7cm,求BD的长。
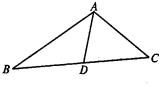
查看答案和解析>>
科目:czsx
来源:北京期中题
题型:证明题
复习“全等三角形”的知识时,老师布置了一道作业题:“如下图①,已知在△ABC中,AB=AC,P是△ABC内部任意一点,将AP绕A顺时针旋转至AQ,使得∠QAP=∠BAC,连接BQ、CP,则BQ=CP.”
(1)小亮是个爱动脑筋的同学,他通过对图①的分析,证明了△ABQ≌△ACP,从而证得BQ=CP.请你帮小亮完成证明.
(2)之后,小亮又将点P移到等腰三角形ABC之外,原题中的条件不变,“BQ=CP”仍然成立吗?若成立,请你就图②给出证明.若不成立,请说明理由.
查看答案和解析>>
科目:czsx
来源:2008-2009学年北京市八一中学九年级(上)期中数学模拟试卷(解析版)
题型:解答题
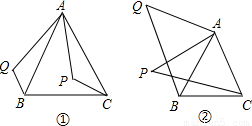
复习“全等三角形”的知识时,老师布置了一道作业题:“如下图①,已知在△ABC中,AB=AC,P是△ABC内部任意一点,将AP绕A顺时针旋转至AQ,使得∠QAP=∠BAC,连接BQ、CP,则BQ=CP.”
(1)小亮是个爱动脑筋的同学,他通过对图①的分析,证明了△ABQ≌△ACP,从而证得BQ=CP.请你帮小亮完成证明.
(2)之后,小亮又将点P移到等腰三角形ABC之外,原题中的条件不变,“BQ=CP”仍然成立吗?若成立,请你就图②给出证明.若不成立,请说明理由.
查看答案和解析>>
科目:czsx
来源:数学教研室
题型:044
如下图,已知在△ABC中,AD=DC,∠AFE=∠ADE,∠C=∠BAD.求证:ED=DF.

查看答案和解析>>
科目:czsx
来源:2009年浙江省湖州市中考数学试题
题型:047
如下图:已知在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E,F.
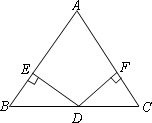
(1)求证:△BED≌△CFD;
(2)若∠A=90°,求证:四边形DFAE是正方形.
查看答案和解析>>
科目:czsx
来源:四川省期末题
题型:填空题
如下图,已知在△ABC中,AD、AE分别是边BC上的高线和中线,AB=9cm,AC=7cm,BC=8cm则DE的长为( )。
查看答案和解析>>
科目:czsx
来源:
题型:

如图,已知在△ABC中,AB=AC,∠A=30°,则外角∠BCD=
105
105
度.
查看答案和解析>>
科目:czsx
来源:
题型:
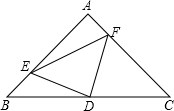
已知在△ABC中,∠A=90°,AB=AC,D为BC的中点.
(1)如图,E、F分别是AB,AC上的动点,且BE=AF,求证:△DEF为等腰直角三角形;
(2)在(1)的条件下,四边形AEDF的面积是否变化,证明你的结论;
(3)若E、F分别为AB,CA延长线上的点,仍有BE=AF,其他条件不变,那么△DEF是否仍为等腰直角三角形?证明你的结论.
查看答案和解析>>
科目:czsx
来源:
题型:

如图,已知在△ABC中,EF平行于CD,G在AC边上,∠1=∠2,求证:∠AGD=∠ACB.
查看答案和解析>>
科目:czsx
来源:
题型:

如图,已知在△ABC中,点D为AC上一点,∠C=∠ABD,BD=3,BC=4,S
△ABD=27,则S
△BCD=
21
21
.
查看答案和解析>>
科目:czsx
来源:
题型:
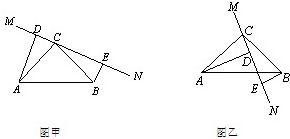
26、如图甲,已知在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.
(1)说明△ADC≌△CEB.
(2)说明AD+BE=DE.
(3)已知条件不变,将直线MN绕点C旋转到图乙的位置时,若DE=3、AD=5.5,则BE=
2.5
.
查看答案和解析>>
科目:czsx
来源:
题型:
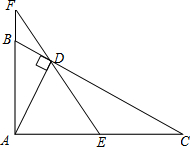
如图所示,已知在△ABC中,∠BAC=90°,AD⊥BC,E是AC的中点,ED交AB延长线于F,求证:
=
.
查看答案和解析>>
科目:czsx
来源:
题型:
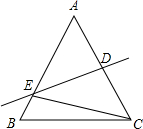
(2013•金山区二模)如图,已知在△ABC中,DE是AC的垂直平分线,交AC于点D,AB于点E,若BC=8,△BCE的周长为
21,cos∠B=
.
求:(1)AB的长;
(2)AC的长.
查看答案和解析>>
科目:czsx
来源:
题型:阅读理解
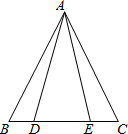
阅读并填空:如图,已知在△ABC中,AB=AC,点D、E在边BC上,且AD=AE.试说明BD=CE的理由.
解:因为AB=AC,
所以
∠B=∠C
∠B=∠C
(等边对等角).
因为
AD=AE
AD=AE
,
所以∠AED=∠ADE(等边对等角).
在△ABE与△ACD中,
| | _____________ | | ∠AED=∠ADE | | AB=AC. |
| |
所以△ABE≌△ACD(
AAS
AAS
)
所以
BE=CD
BE=CD
(全等三角形对应边相等),
所以
BE-DE=CD-DE
BE-DE=CD-DE
(等式性质).
即BD=CE.
查看答案和解析>>
科目:czsx
来源:
题型:

如图,已知在△ABC中,∠A=∠B
(1)请你添加一个与直线AB有关的条件,由此可推得CE是∠ACD的角平分线(只添加条件,不说理由);
(2)请你添加一个与∠A有关的条件,由此可推得CE是∠ACD的角平分线.(要写出理由)
查看答案和解析>>
科目:czsx
来源:
题型:
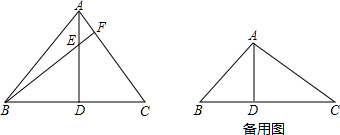
已知在△ABC中,AD⊥BC,垂足为D点在边BC上,BF⊥AC分别交射线DA、射线CA于点E、F,若BD=4,∠BAD=45°.
(1)如图:若∠BAC是锐角,则点F在边AC上,
①求证:△BDE≌△ADC;
②若DC=3,求AE的长;
(2)若∠BAC是钝角,AE=1,求AC的长.
查看答案和解析>>
科目:czsx
来源:
题型:

如图,已知在△ABC中,AB=AC,∠BAC=90°,点D是BC上的任意一点,探究:BD
2+CD
2与AD
2的关系,并证明你的结论.
查看答案和解析>>
科目:czsx
来源:
题型:
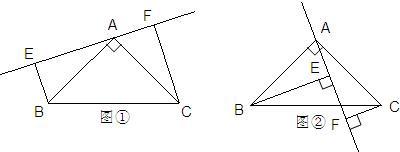
24、如图,已知在△ABC中,AB=AC,∠BAC=90°,分别过B、C向过A的直线作垂线,垂足分别为E、F.
(1)如图①过A的直线与斜边BC不相交时,求证:EF=BE+CF;
(2)如图②过A的直线与斜边BC相交时,其他条件不变,若BE=10,CF=3,求:FE长.
查看答案和解析>>

 26、
26、 复习“全等三角形”的知识时,老师布置了一道作业题:“如下图①,已知在△ABC中,AB=AC,P是△ABC内部任意一点,将AP绕A顺时针旋转至AQ,使得∠QAP=∠BAC,连接BQ、CP,则BQ=CP.”
复习“全等三角形”的知识时,老师布置了一道作业题:“如下图①,已知在△ABC中,AB=AC,P是△ABC内部任意一点,将AP绕A顺时针旋转至AQ,使得∠QAP=∠BAC,连接BQ、CP,则BQ=CP.”

![]() =
=![]() 。
。
![]() =
=![]() ,一般只要证BD、DC与AB、AC
,一般只要证BD、DC与AB、AC![]()
![]() 中,AC恰是BD、DC、AB的第四比例项,所以考虑过点C作CE//AD,交
中,AC恰是BD、DC、AB的第四比例项,所以考虑过点C作CE//AD,交![]() =
=![]()
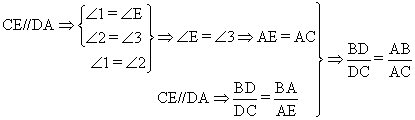 。
。


 已知在△ABC中,∠A=90°,AB=AC,D为BC的中点.
已知在△ABC中,∠A=90°,AB=AC,D为BC的中点.
 (2013•金山区二模)如图,已知在△ABC中,DE是AC的垂直平分线,交AC于点D,AB于点E,若BC=8,△BCE的周长为
(2013•金山区二模)如图,已知在△ABC中,DE是AC的垂直平分线,交AC于点D,AB于点E,若BC=8,△BCE的周长为 阅读并填空:如图,已知在△ABC中,AB=AC,点D、E在边BC上,且AD=AE.试说明BD=CE的理由.
阅读并填空:如图,已知在△ABC中,AB=AC,点D、E在边BC上,且AD=AE.试说明BD=CE的理由. 如图,已知在△ABC中,∠A=∠B
如图,已知在△ABC中,∠A=∠B
