
科目:czsx 来源: 题型:
我市水产养殖专业户王大爷承包了30亩水塘,分别养殖甲鱼和鳜鱼.有关成本和销售额见下表:

1.2011年,王大爷养殖甲鱼20亩,鳜鱼10亩.王大爷这一年共收益多少万元?(收益=销售额-成本)
2.2011年,王大爷继续用这30亩水塘全部养殖甲鱼和鳜鱼,计划投入成本不超过70万元,若每亩养殖的成本、销售额与2011年相同,要获得最大收益,则他应养殖甲鱼和鳜鱼各多少亩?
3.已知甲鱼每亩需要饲料500 kg,鳜鱼每亩需要饲料700 kg.根据(2)中的养殖亩数,为了节约运输成本,实际使用的运输车辆每次装载饲料的总量是原计划每次装载总量的2倍,结果运输养殖所需全部饲料比原计划减少了2次,王大爷原定的运输车辆每次可装载多少饲料?
科目:czsx 来源: 题型:
如图①,已知抛物线y=ax2+bx+3(a≠0)与x轴交于点A(1,0)和点B(-3,0),与y轴交于点C.
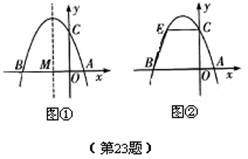
1.求抛物线的解析式;
2.设抛物线的对称轴与x轴交于点M,问在对称轴上是否存在点P,使△CMP为等腰三角形?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
3.如图②,若点E为第二象限抛物线上一动点,连接BE、CE,求四边形BOCE面积的最大值,并求此时的点E的坐标.
科目:czsx 来源: 题型:
如图,在△ABC中,AB=5,BC=3,AC=4,动点E(与点A、C不重合)在AC边上,EF∥AB交BC于点F.
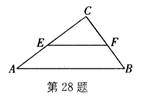
1.当△ECF的面积与四边形EABF的面积相等时,求CE的长
2.当△ECF的周长与四边形EABF的周长相等时,求CE的长
3.试问在AB上是否存在点P,使得△EFP为等腰直角三角形?若不存在,请简要说明理由;若存在,请求出EF的长.
科目:czsx 来源: 题型:
如图,正方形ABCD内接于⊙O,⊙O的半径为2,以圆心O为顶点作 ∠MON,使∠MON=90°,OM、ON分别与⊙O交于点E、F,与正方形ABCD的边交于点G、H, 则由OE、OF、及正方形ABCD的边围成的图形(阴影部分)的面积S= .
科目:czsx 来源: 题型:
如图,在下列矩形ABCD中,已知:AB=a,BC=b(a<b),假定顶点在矩形边上的菱形叫做矩形的内接菱形,现给出(Ⅰ)、(Ⅱ)、(Ⅲ)三个命题:
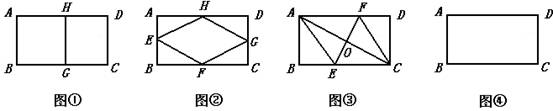
命题(Ⅰ):图①中,若AH=BG=AB,则四边形ABGH是矩形ABCD的内接菱形;
命题(Ⅱ):图②中,若点E、F、G和H分别是AB、BC、CD和DE的中点,则四边形EFGH是矩形ABCD的内接菱形;
命题(Ⅲ):图③中,若EF垂直平分对角线AC,变BC于点E,交AD于点F,交AC于点O,则四边形AECF是矩形ABCD的内接菱形.
请解决下列问题:
1.命题(Ⅰ)、(Ⅱ)、(Ⅲ)都是真命题吗?请你在其中选择一个,并证明它是真命题或假命题;
2.画出一个新的矩形内接菱形(即与你在(1)中所确认的,但不全等的内接菱形).
3.试探究比较图①,②,③中的四边形ABGH、EFGH、AECF的面积大小关系
科目:czsx 来源: 题型:
如图, 已知抛物线![]() 与y轴相交于C,与x轴相交于A、B,点A的坐标为(-1,0),点C的坐标为(0,-3),抛物线的顶点为D.
与y轴相交于C,与x轴相交于A、B,点A的坐标为(-1,0),点C的坐标为(0,-3),抛物线的顶点为D.
1.求抛物线的解析式和顶点D的坐标
2.二次函数的图像上是否存在点P,使得S△PAB=8S△ABD?若存在,求出P点坐标;若不存在,请说明理由;
3.若抛物线的对称轴与x轴交于E点,点F在直线BC上,点M在的二次函数图像上,如果以点F、M、D、E为顶点的四边形是平行四边形,请你求出符合条件的点M的坐标.
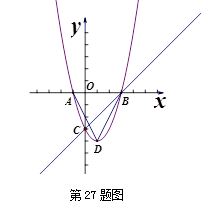
科目:czsx 来源: 题型:
某地区准备修建一座高AB=6m的过街天桥,已知天桥的坡面AC与地面BC的夹角∠ACB的余弦值为![]() ,则坡面AC的长度为( )
,则坡面AC的长度为( )

A.8 B.9 C.10 D.12
科目:czsx 来源: 题型:
如图,两颗树的高度分别为AB=6m,CD=8m,两树的根部间的距离AC=4m,小强沿着 正对这两棵树的方向从左向右前进,如果小强的眼睛与地面的距离为1.6m,当小强与树AB的距离小于多少时,就不能看到树CD的树顶D?

科目:czsx 来源: 题型:
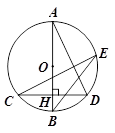
如图,在⊙O中,直径AB⊥弦CD于点H,E是⊙O上的点,若∠BEC=25°,则∠BAD的度数为
A. 65° B. 50°![]() C. 25° D. 12.5°
C. 25° D. 12.5°
科目:czsx 来源: 题型:
如图,在直角坐标系中,直线![]() 分别与x轴、y轴交于点M、N,点A、B分别在y轴、x轴上,且∠B=30°,AB=4,将△ABO绕原点O顺时针转动一周,当AB与直线MN平行时点A的坐标为 ▲ .
分别与x轴、y轴交于点M、N,点A、B分别在y轴、x轴上,且∠B=30°,AB=4,将△ABO绕原点O顺时针转动一周,当AB与直线MN平行时点A的坐标为 ▲ .

科目:czsx 来源: 题型:
小亮和小刚进行赛跑训练,他们选择了一个土坡,按同一路线同时出发,从坡底跑到坡顶再原路返回坡底.他们俩上坡的平均速度不同,下坡的平均速度则是各自上坡平均速度的1.5倍.设两人出发x min后距出发点的距离为y m.图中折线表示小亮在整个训练中y与x的函数关系,其中A点在x轴上,M点坐标为(2,0).

1.小亮下坡的速度是 ▲ m/min;= ▲
2.求出AB所在直线的函数关系式
3.如果小刚上坡平均速度是小亮上坡平均速度的一半,那么两人出发后多长时间第一次相遇?
科目:czsx 来源: 题型:
如图,在直角梯形ABCD中,AB∥CD,∠A=90°,∠B=45°,AB=4![]() , BC=3,F是DC上一点,且CF=
, BC=3,F是DC上一点,且CF= , E,是线段AB上一动点,将射线EF绕点E顺时针旋转45°交BC边于点G.
, E,是线段AB上一动点,将射线EF绕点E顺时针旋转45°交BC边于点G.
1.直接写出线段AD和CD的长;
2.设AE=x,当x为何值时△BEG是等腰三角形;
3.当△BEG是等腰三角形时,将△BEG沿EG折叠,得到△B’EG,求△B’EG与五边形AEGCD重叠部分的面积.
