
科目:czsx 来源:2013届江苏省无锡市八年级下学期期中考试数学卷(解析版) 题型:解答题
如图(1),△ABC与△EFD为等腰直角三角形,AC与DE重合,AB=AC=EF=3,∠BAC=∠DEF=90º,固定△ABC,将△DEF绕点A顺时针旋转,当DF边与AB边重合时,旋转中止.现不考虑旋转开始和结束时重合的情况,设DE,DF(或它们的延长线)分别交BC(或它的延长线) 于G,H点,如图(2)
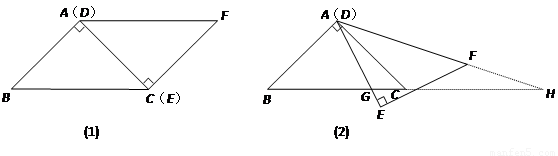
(1)问:始终与△AGC相似的三角形有 及 ;
(2)设CG=x,BH=y,求y关于x的函数关系式(只要求根据图(2)的情形说明理由);
(3)问:当x为何值时,△AGH是等腰三角形。
【解析】(1)根据△ABC与△EFD为等腰直角三角形,AC与DE重合,利用相似三角形的判定定理即可得出结论.
(2)由△AGC∽△HAB,利用其对应边成比例列出关于x、y的关系式:3:y=x:3即可.
(3)此题要采用分类讨论的思想,当CG<1/2BC时,当CG=1/2BC时,当CG>1/2BC时分别得出即可
科目:czsx 来源: 题型:
如图(1),△ABC与△EFD为等腰直角三角形,AC与DE重合,AB=AC=EF=3,∠BAC=∠DEF=90º,固定△ABC,将△DEF绕点A顺时针旋转,当DF边与AB边重合时,旋转中止.现不考虑旋转开始和结束时重合的情况,设DE,DF(或它们的延长线)分别交BC(或它的延长线) 于G,H点,如图(2)

(1)问:始终与△AGC相似的三角形有 及 ;
(2)设CG=x,BH=y,求y关于x的函数关系式(只要求根据图(2)的情形说明理由);
(3)问:当x为何值时,△AGH是等腰三角形。
【解析】(1)根据△ABC与△EFD为等腰直角三角形,AC与DE重合,利用相似三角形的判定定理即可得出结论.
(2)由△AGC∽△HAB,利用其对应边成比例列出关于x、y的关系式:3:y=x:3即可.
(3)此题要采用分类讨论的思想,当CG<1/2BC时,当CG=1/2BC时,当CG>1/2BC时分别得出即可
科目:czsx 来源: 题型:
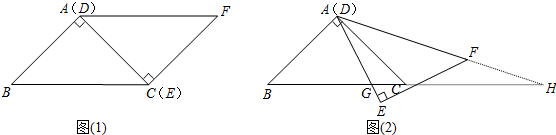
科目:czsx 来源: 题型:

科目:czsx 来源: 题型:

科目:czsx 来源: 题型:

科目:czsx 来源: 题型:
如图(1),△ABC与△EFD为等腰直角三角形,AC与DE重合,AB=AC=EF=9,∠BAC=∠DEF=90º,固定△ABC,将△DEF绕点A顺时针旋转,当DF边与AB边重合时,旋转中止.现不考虑旋转开始和结束时重合的情况,设DE,DF(或它们的延长线)分别交BC(或它的延长线) 于G,H点,如图(2)
(1)问:始终与△AGC相似的三角形有 及 ;
(2)设CG=x,BH=y,求y关于x的函数关系式(只要求根据图(2)的情形说明理由)
(3)问:当x为何值时,△AGH是等腰三角形.
科目:czsx 来源: 题型:

科目:czsx 来源: 题型:
如图(1),△ABC与△EFD为等腰直角三角形,AC与DE重合,AB=AC=EF=9,∠BAC=∠DEF=90º,固定△ABC,将△DEF绕点A顺时针旋转,当DF边与AB边重合时,旋转中止.现不考虑旋转开始和结束时重合的情况,设DE,DF(或它们的延长线)分别交BC(或它的延长线) 于G,H点,如图(2)

(1)问:始终与△AGC相似的三角形有 及 ;
(2)设CG=x,BH=y,求y关于x的函数关系式(只要求根据图(2)的情形说明理由)
(3)问:当x为何值时,△AGH是等腰三角形.
科目:czsx 来源:2011年河北省衡水市五校九年级下学期第三次月考数学卷 题型:解答题
如图(1),△ABC与△EFD为等腰直角三角形,AC与DE重合,AB=EF=9,∠BAC=∠DEF=90°,固定△ABC,将△EFD绕点A 顺时针旋转,当DF边与AB边重合时,旋转中止。不考虑旋转开始和结束时重合的情况,设DE、DF(或它们的延长线)分别交BC(或它的延长线)于G、H点,如图(2)。
1.问:始终与△AGC相似的三角形有 及 ;
2.设CG=x,BH=y,求y关于x的函数关系式(只要求根据2的情况说明理由);
3.问:当x为何值时,△AGH是等腰三角形?

科目:czsx 来源:2011年广东省东莞市中考数学真题试卷 题型:选择题
如图(1),△ABC与△EFD为等腰直角三角形,AC与DE重合,AB=AC=EF=9,∠BAC=∠DEF=90º,固定△ABC,将△DEF绕点A顺时针旋转,当DF边与AB边重合时,旋转中止.现不考虑旋转开始和结束时重合的情况,设DE,DF(或它们的延长线)分别交BC(或它的延长线) 于G,H点,如图(2)

(1)问:始终与△AGC相似的三角形有 及 ;
(2)设CG=x,BH=y,求y关于x的函数关系式(只要求根据图(2)的情形说明理由)
(3)问:当x为何值时,△AGH是等腰三角形.
科目:czsx 来源:2011-2012年河北省衡水市五校九年级第三次联考数学卷 题型:解答题
(本小题满分12分)
如图(1),△ABC与△EFD为等腰直角三角形,AC与DE重合,AB=EF=9,∠BAC=∠DEF=90°,固定△ABC,将△EFD绕点A 顺时针旋转,当DF边与AB边重合时,旋转中止。不考虑旋转开始和结束时重合的情况,设DE、DF(或它们的延长线)分别交BC(或它的延长线)于G、H点,如图(2)。
【小题1】(1)问:始终与△AGC相似的三角形有 及 ;
【小题2】(2)设CG=x,BH=y,求y关于x的函数关系式(只要求根据2的情况说明理由);
【小题3】(3)问:当x为何值时,△AGH是等腰三角形?
科目:czsx 来源:2013年初中数学单元提优测试卷-相似的判定(解析版) 题型:解答题
如图(1),△ABC与△EFD为等腰直角三角形,AC与DE重合,AB=EF,∠BAC=∠DEF=90°,固定△ABC,将△EFD绕点A 顺时针旋转,当DF边与AB边重合时,旋转中止.不考虑旋转开始和结束时重合的情况,设DE、DF(或它们的延长线)分别交BC(或它的延长线)于G、H点,如图(2).

(1)问:始终与△AGC相似的三角形有 ;
(2)请选择(1)中的一组相似三角形加以证明.
科目:czsx 来源:2013年初中数学单元提优测试卷-相似的判定(带解析) 题型:解答题
如图(1),△ABC与△EFD为等腰直角三角形,AC与DE重合,AB=EF,∠BAC=∠DEF=90°,固定△ABC,将△EFD绕点A 顺时针旋转,当DF边与AB边重合时,旋转中止.不考虑旋转开始和结束时重合的情况,设DE、DF(或它们的延长线)分别交BC(或它的延长线)于G、H点,如图(2).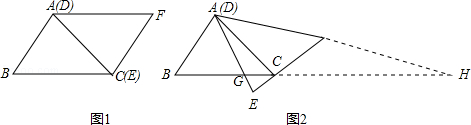
(1)问:始终与△AGC相似的三角形有 ;
(2)请选择(1)中的一组相似三角形加以证明.
科目:czsx 来源: 题型:
科目:czsx 来源: 题型:
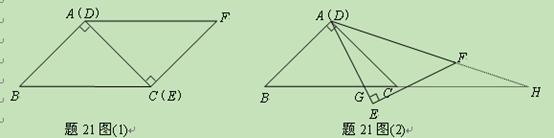
如图(1),△ABC与△EFD为等腰直角三角形,AC与DE重合,AB=AC=EF=9,∠BAC=∠DEF=90º,固定△ABC,将△DEF绕点A顺时针旋转,当DF边与AB边重合时,旋转中止.现不考虑旋转开始和结束时重合的情况,设DE,DF(或它们的延长线)分别交BC(或它的延长线) 于G,H点,如图(2)
(1)问:始终与△AGC相似的三角形有 及 ;
(2)设CG=x,BH=y,求y关于x的函数关系式(只要求根据图(2)的情形说明理由)
(3)问:当x为何值时,△AGH是等腰三角形.
科目:czsx 来源:2011年初中毕业升学考试(湖南娄底卷)数学 题型:解答题
如图(1),△ABC与△EFD为等腰直角三角形,AC与DE重合,AB=AC=EF=9,∠BAC=∠DEF=90º,固定△ABC,将△DEF绕点A顺时针旋转,当DF边与AB边重合时,旋转中止.现不考虑旋转开始和结束时重合的情况,设DE,DF(或它们的延长线)分别交BC(或它的延长线) 于G,H点,如图(2)

(1)问:始终与△AGC相似的三角形有 及 ;
(2)设CG=x,BH=y,求y关于x的函数关系式(只要求根据图(2)的情形说明理由)
(3)问:当x为何值时,△AGH是等腰三角形.
科目:czsx 来源:2011-2012学年江苏省无锡市羊尖中学八年级下学期期中考试数学卷(带解析) 题型:解答题
如图(1),△ABC与△EFD为等腰直角三角形,AC与DE重合,AB=AC=EF=3,∠BAC=∠DEF=90º,固定△ABC,将△DEF绕点A顺时针旋转,当DF边与AB边重合时,旋转中止.现不考虑旋转开始和结束时重合的情况,设DE,DF(或它们的延长线)分别交BC(或它的延长线) 于G,H点,如图(2)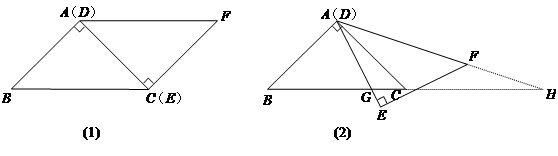
(1)问:始终与△AGC相似的三角形有 及 ;
(2)设CG=x,BH=y,求y关于x的函数关系式(只要求根据图(2)的情形说明理由);
(3)问:当x为何值时,△AGH是等腰三角形。
科目:czsx 来源:2012届浙江金华十八中九年级上期期中调研数学试卷(带解析) 题型:解答题
如图(1)△ABC与△EFD为等腰直角三角形,AC与DE重合,AB=AC=EF=9,∠BAC=∠DEF=90º,固定△ABC,将△DEF绕点A顺时针旋转,当DF边与AB边重合时,旋转中止.现不考虑旋转开始和结束时重合的情况,设DE,DF(或它们的延长线)分别交BC(或它的延长线) 于G,H点,如图(2)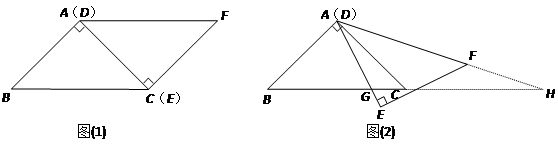
(1)问:始终与△AGC相似的三角形有 及 ;
(2)设CG=x,BH=y,求y关于x的函数关系式(只要求根据图(2)的情形说明理由)
(3)问:当x为何值时,△AGH是等腰三角形.
科目:czsx 来源:2011年初中毕业升学考试(广东卷)数学 题型:解答题
如图(1),△ABC与△EFD为等腰直角三角形,AC与DE重合,AB=AC=EF=9,∠BAC=∠DEF=90º,固定△ABC,将△DEF绕点A顺时针旋转,当DF边与AB边重合时,旋转中止.现不考虑旋转开始和结束时重合的情况,设DE,DF(或它们的延长线)分别交BC(或它的延长线) 于G,H点,如图(2)

(1)问:始终与△AGC相似的三角形有 及 ;
(2)设CG=x,BH=y,求y关于x的函数关系式(只要求根据图(2)的情形说明理由)
(3)问:当x为何值时,△AGH是等腰三角形.