精英家教网 >
试题搜索列表 >已知在△ABC中,∠ACB=90°,CA=CB=6√2,CD⊥AB于D,点E在直线
已知在△ABC中,∠ACB=90°,CA=CB=6√2,CD⊥AB于D,点E在直线答案解析
科目:czsx
来源:
题型:
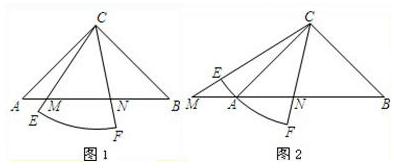
25、已知Rt△ABC中,∠ACB=90°,CA=CB,有一个圆心角为45°,半径的长等于CA的扇形CEF绕点C旋转,且直线CE,CF分别与直线AB交于点M,N.
(Ⅰ)当扇形CEF绕点C在∠ACB的内部旋转时,如图1,求证:MN
2=AM
2+BN
2;
(思路点拨:考虑MN
2=AM
2+BN
2符合勾股定理的形式,需转化为在直角三角形中解决.可将△ACM沿直线CE对折,得△DCM,连DN,只需证DN=BN,∠MDN=90°就可以了.请你完成证明过程.)
(Ⅱ)当扇形CEF绕点C旋转至图2的位置时,关系式MN
2=AM
2+BN
2是否仍然成立?若成立,请证明;若不成立,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
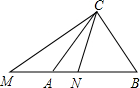
已知Rt△ABC中,∠ACB=90°,CA=CB,M在BA延长线上,N在AB上,且∠MCN=45°,AM=2,BN=3,则MN=
.
查看答案和解析>>
科目:czsx
来源:
题型:

20、如图,已知Rt△ABC中,∠ACB=90°,CA=CB,D是AC上一点,E在BC的延长线上,且AE=BD,BD的延长线与AE交于点F.试通过观察、测量、猜想等方法来探索BF与AE有何特殊的位置关系,并说明你猜想的正确性.
查看答案和解析>>
科目:czsx
来源:
题型:
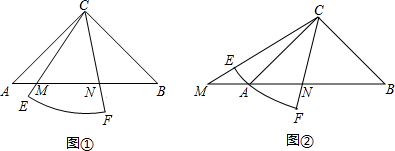
(2013•桥西区模拟)已知Rt△ABC中,∠ACB=90°,CA=CB,有一个圆心角为45°,半径的长等于CA的扇形CEF绕点C旋转,且直线CE,CF分别与直线AB交于点M,N.
(1)当扇形CEF绕点C在∠ACB的内部旋转时,如图①,求证:MN
2=AM
2+BN
2;
思路点拨:考虑MN
2=AM
2+BN
2符合勾股定理的形式,需转化为在直角三角形中解决.可将△ACM沿直线CE对折,得△DCM,连DN,只需证DN=BN,∠MDN=90°就可以了.
请你完成证明过程:
(2)当扇形CEF绕点C旋转至图②的位置时,关系式MN
2=AM
2+BN
2是否仍然成立?若成立,请证明;若不成立,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
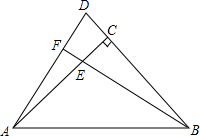
已知Rt△ABC中,∠ACB=90°,CA=CB,点D在BC的延长线上,点E在AC上,且CD=CE,延长BE交AD于点F,求证:BF⊥AD.
查看答案和解析>>
科目:czsx
来源:
题型:
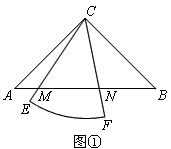
已知Rt△ABC中,∠ACB=90°,CA=CB,有一个圆心角为45°,半径长等于CA的扇形CEF绕点C旋转,直线CE、CF分别与直线AB交于点M、N.
(1)如图①,当AM=BN时,将△ACM沿CM折叠,点A落在弧EF的中点P处,再将△BCN沿CN折叠,点B也恰好落在点P处,此时,PM=AM,PN=BN,△PMN的形状是
.线段AM、BN、MN之间的数量关系是
;
(2)如图②,当扇形CEF绕点C在∠ACB内部旋转时,线段MN、AM、BN之间的数量关系是
.试证明你的猜想;
(3)当扇形CEF绕点C旋转至图③的位置时,线段MN、AM、BN之间的数量关系是
.(不要求证明)

查看答案和解析>>
科目:czsx
来源:期末题
题型:解答题
如图,已知Rt△ABC中,∠ACB=90°,CA=CB,D是AC上一点,E在BC的延长线上,且AE=BD,BD的延长线与AE交于点F.试通过观察、测量、猜想等方法来探索BF与AE有何特殊的位置关系,并说明你猜想的正确性.
查看答案和解析>>
科目:czsx
来源:天津中考真题
题型:解答题
已知Rt△ABC中,∠ACB=90°,CA=CB,有一个圆心角为45°,半径的长等于CA的扇形CEF绕点C旋转,且直线CE,CF分别与直线AB交于点M,N。
(1)当扇形CEF绕点C在∠ACB的内部旋转时,如图1,求证:MN2=AM2+BN2;(思路点拨:考虑MN2=AM2+BN2符合勾股定理的形式,需转化为在直角三角形中解决,可将△ACM沿直线CE对折,得△DCM,连DN,只需证DN=BN,∠MDN=90°就可以了,请你完成证明过程。)
(2)当扇形CEF绕点C旋转至图2的位置时,关系式MN2=AM2+BN2是否仍然成立?若成立,请证明;若不成立,请说明理由。
查看答案和解析>>
科目:czsx
来源:不详
题型:解答题
如图,已知Rt△ABC中,∠ACB=90°,CA=CB,D是AC上一点,E在BC的延长线上,且AE=BD,BD的延长线与AE交于点F.试通过观察、测量、猜想等方法来探索BF与AE有何特殊的位置关系,并说明你猜想的正确性.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
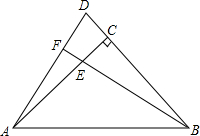 已知Rt△ABC中,∠ACB=90°,CA=CB,点D在BC的延长线上,点E在AC上,且CD=CE,延长BE交AD于点F,求证:BF⊥AD.
已知Rt△ABC中,∠ACB=90°,CA=CB,点D在BC的延长线上,点E在AC上,且CD=CE,延长BE交AD于点F,求证:BF⊥AD.
查看答案和解析>>
科目:czsx
来源:期末题
题型:解答题
如图,已知Rt△ABC中,∠ACB=90°,CA=CB,D是AC上一点,E在BC的延长线上,且AE=BD,BD的延长线与AE交于点F.试通过观察、测量、猜想等方法来探索BF与AE有何特殊的位置关系,并说明你猜想的正确性.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
 如图,已知Rt△ABC中,∠ACB=90°,CA=CB,D是AC上一点,E在BC的延长线上,且AE=BD,BD的延长线与AE交于点F.试通过观察、测量、猜想等方法来探索BF与AE有何特殊的位置关系,并说明你猜想的正确性.
如图,已知Rt△ABC中,∠ACB=90°,CA=CB,D是AC上一点,E在BC的延长线上,且AE=BD,BD的延长线与AE交于点F.试通过观察、测量、猜想等方法来探索BF与AE有何特殊的位置关系,并说明你猜想的正确性.
查看答案和解析>>
科目:czsx
来源:
题型:填空题
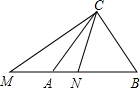 已知Rt△ABC中,∠ACB=90°,CA=CB,M在BA延长线上,N在AB上,且∠MCN=45°,AM=2,BN=3,则MN=________.
已知Rt△ABC中,∠ACB=90°,CA=CB,M在BA延长线上,N在AB上,且∠MCN=45°,AM=2,BN=3,则MN=________.
查看答案和解析>>
科目:czsx
来源:
题型:
已知在△ABC中,∠ACB=90°,∠B=30°,AB=2,则AC=
.
查看答案和解析>>
科目:czsx
来源:
题型:
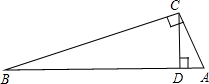
如图,已知在△ABC中,∠ACB=90°,CD⊥AB,垂足为D,AC=5,BC=12,求:
(1)AB的长;
(2)△ABC的面积;
(3)CD的长.
查看答案和解析>>
科目:czsx
来源:
题型:
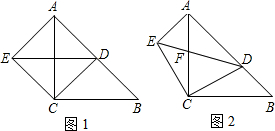
已知在△ABC中,∠ACB=90°,AC=BC,点D是边AB上一点,AE⊥AB,且AE=BD,DE与AC相交于点F.
(1)若点D是AB的中点(如图1),试判断△CDE的形状,并证明你的结论;
(2)若点D不是AB的中点(如图2),那么(1)中的结论是否仍然成立?如果一定成立,请加以证明;如果不一定成立,请说明理由;
(3)若AD=AC,那么△AEF是
三角形.
查看答案和解析>>
科目:czsx
来源:
题型:
数形结合作为一种数学思想方法,数形结合的应用大致又可分为两种情形:或者借助于数的精确性来阐明形的某些属性,即“以数解形”;或者借助形的几何直观性来阐明数之间的某种关系,即“以形助数”.
如浙教版九上课本第109页作业题第2题:如图1,已知在△ABC中,∠ACB=90°,CD⊥AB,D为垂足.易证得两个结论:(1)AC•BC=AB•CD (2)AC
2=AD•AB
(1)请你用数形结合的“以数解形”思想来解:如图2,已知在△ABC中(AC>BC),∠ACB=90°,CD⊥AB,D为垂足,CM平分∠ACB,且BC、AC是方程x
2-14x+48=0的两个根,求AD、MD的长.
(2)请你用数形结合的“以形助数”思想来解:设a、b、c、d都是正数,满足a:b=c:d,且a最大.求证:a+d>b+c(提示:不访设AB=a,CD=d,AC=b,BC=c,构造图1)
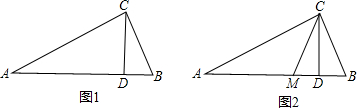
查看答案和解析>>
科目:czsx
来源:
题型:

如图,已知在△ABC中,∠ACB=90°,在AB上截取AE=AC,BD=BC.求证:∠DCE=45°.
查看答案和解析>>
科目:czsx
来源:
题型:
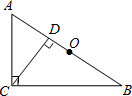
如图,已知在△ABC中,∠ACB=90゜,AB=10,BC=8,CD⊥AB于D,O为AB的中点.
(1)以C为圆心,6为半径作圆C,试判断点A、D、B与⊙C的位置关系;
(2)⊙C的半径为多少时,点D在⊙C上?
查看答案和解析>>
科目:czsx
来源:
题型:

如图,已知在△ABC中,∠ACB=90°,CD为AB边上的高,AD=4,BD=
,则AC的长为
,CD的长为
.
查看答案和解析>>


 20、如图,已知Rt△ABC中,∠ACB=90°,CA=CB,D是AC上一点,E在BC的延长线上,且AE=BD,BD的延长线与AE交于点F.试通过观察、测量、猜想等方法来探索BF与AE有何特殊的位置关系,并说明你猜想的正确性.
20、如图,已知Rt△ABC中,∠ACB=90°,CA=CB,D是AC上一点,E在BC的延长线上,且AE=BD,BD的延长线与AE交于点F.试通过观察、测量、猜想等方法来探索BF与AE有何特殊的位置关系,并说明你猜想的正确性.





 如图,已知Rt△ABC中,∠ACB=90°,CA=CB,D是AC上一点,E在BC的延长线上,且AE=BD,BD的延长线与AE交于点F.试通过观察、测量、猜想等方法来探索BF与AE有何特殊的位置关系,并说明你猜想的正确性.
如图,已知Rt△ABC中,∠ACB=90°,CA=CB,D是AC上一点,E在BC的延长线上,且AE=BD,BD的延长线与AE交于点F.试通过观察、测量、猜想等方法来探索BF与AE有何特殊的位置关系,并说明你猜想的正确性. 已知Rt△ABC中,∠ACB=90°,CA=CB,M在BA延长线上,N在AB上,且∠MCN=45°,AM=2,BN=3,则MN=________.
已知Rt△ABC中,∠ACB=90°,CA=CB,M在BA延长线上,N在AB上,且∠MCN=45°,AM=2,BN=3,则MN=________.
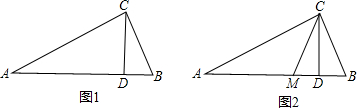
 如图,已知在△ABC中,∠ACB=90゜,AB=10,BC=8,CD⊥AB于D,O为AB的中点.
如图,已知在△ABC中,∠ACB=90゜,AB=10,BC=8,CD⊥AB于D,O为AB的中点.