已知cd为三角形abc的高ac cd=bc ad答案解析
科目:czsx
来源:
题型:
(2013•沈阳)已知等边三角形ABC的高为4,在这个三角形所在的平面内有一点P,若点P到AB的距离是1,点P到AC的距离是2,则点P到BC的最小距离和最大距离分别是
1,7
1,7
.
查看答案和解析>>
科目:czsx
来源:
题型:
15、规定三角形的三条内角平分线的交点叫三角形的内心.
(1)已知I为三角形ABC的内心,连接AI交三角形ABC的外接圆于点D,如图所示,连接BD和CD,求证:BD=CD=ID.

(2)己知三角形ABC,AD平分∠BAC且与它的外接圆交于点D,在线段AD上有一点I满足BD=ID.试问点I是否是三角形ABC的内心?若是加以证明;若不是,说明理由.

查看答案和解析>>
科目:czsx
来源:2013年初中毕业升学考试(辽宁沈阳卷)数学(解析版)
题型:填空题
已知等边三角形ABC的高为4,在这个三角形所在的平面内有一点P,若点P到AB的距离是1,点P到AC的距离是2,则点P到BC的最小距离和最大距离分别是 .
查看答案和解析>>
科目:czsx
来源:2013年辽宁省辽阳市高级中等学校招生考试数学
题型:022
已知等边三角形ABC的高为4,在这个三角形所在的平面内有一点P,若点P到AB的距离是1,点P到AC的距离是2,则点P到BC的最小距离和最大距离分别是________.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
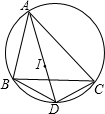
规定三角形的三条内角平分线的交点叫三角形的内心.
(1)已知I为三角形ABC的内心,连接AI交三角形ABC的外接圆于点D,如图所示,连接BD和CD,求证:BD=CD=ID.
(2)己知三角形ABC,AD平分∠BAC且与它的外接圆交于点D,在线段AD上有一点I满足BD=ID.试问点I是否是三角形ABC的内心?若是加以证明;若不是,说明理由.
查看答案和解析>>
科目:czsx
来源:2013年辽宁省沈阳市中考数学试卷(解析版)
题型:填空题
已知等边三角形ABC的高为4,在这个三角形所在的平面内有一点P,若点P到AB的距离是1,点P到AC的距离是2,则点P到BC的最小距离和最大距离分别是 .
查看答案和解析>>
科目:czsx
来源:2006年浙江省宁波市北仑中学保送生招生数学试卷(解析版)
题型:解答题
规定三角形的三条内角平分线的交点叫三角形的内心.
(1)已知I为三角形ABC的内心,连接AI交三角形ABC的外接圆于点D,如图所示,连接BD和CD,求证:BD=CD=ID.

(2)己知三角形ABC,AD平分∠BAC且与它的外接圆交于点D,在线段AD上有一点I满足BD=ID.试问点I是否是三角形ABC的内心?若是加以证明;若不是,说明理由.

查看答案和解析>>
科目:czsx
来源:
题型:
已知等边三角形ABC的高为4,在这个三角形所在的平面内有一点P,若点P到AB的距离是1,点P到AC的距离是2,则点P到BC的最小距离和最大距离分别是 _________
查看答案和解析>>
科目:czsx
来源:
题型:填空题
已知等边三角形ABC的高为4,在这个三角形所在的平面内有一点P,若点P到AB的距离是1,点P到AC的距离是2,则点P到BC的最小距离和最大距离分别是________.
查看答案和解析>>
科目:czsx
来源:
题型:
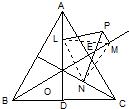
如图所示,已知O为正三角形ABC的高AD、BE、CF的交点,P是△ABC所在平面上的任一点,作PL⊥AD于L,PM⊥BE于M,PN⊥CF于N.试证:PL、PM、PN中较大的一条线段等于其它两条线段的和.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
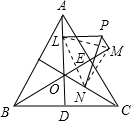 如图所示,已知O为正三角形ABC的高AD、BE、CF的交点,P是△ABC所在平面上的任一点,作PL⊥AD于L,PM⊥BE于M,PN⊥CF于N.试证:PL、PM、PN中较大的一条线段等于其它两条线段的和.
如图所示,已知O为正三角形ABC的高AD、BE、CF的交点,P是△ABC所在平面上的任一点,作PL⊥AD于L,PM⊥BE于M,PN⊥CF于N.试证:PL、PM、PN中较大的一条线段等于其它两条线段的和.
查看答案和解析>>
科目:czsx
来源:
题型:
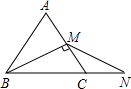
如图所示,已知等边三角形ABC的周长是2a,BM是AC边上的高,N为BC延长线上的一点,且CN=CM,则BN=
.
查看答案和解析>>
科目:czsx
来源:
题型:
如图,已知等边三角形ABC的边长为2,AD是BC边上的高.
(1)在△ABC内部作一个矩形EFGH(如图①),其中E、H分别在边AB、AC上,FG在边BC上.
①设矩形的一边FG=x,那么EF=
;(用含有x的代数式表示)
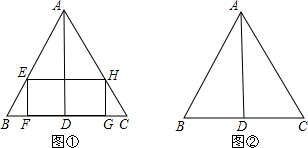
②设矩形的面积为y,当x取何值时,y的值最大,最大值是多少?
(2)当矩形EFGH面积最大时,请在图②中画出此时点E的位置.(要求尺规作图,保留作图痕迹,并简要说明确定点E的方法)
查看答案和解析>>
科目:czsx
来源:
题型:
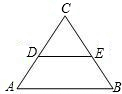
如图,已知等边三角形ABC的边长为2,DE是它的中位线,则下面四个结论:
(1)DE=1;
(2)AB边上的高为
;
(3)△CDE∽△CAB;
(4)△CDE的面积与△CAB面积之比为1:4.
其中正确的有( )
查看答案和解析>>
科目:czsx
来源:
题型:
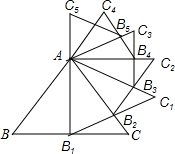
(2013•黑龙江)已知等边三角形ABC的边长是2,以BC边上的高AB
1为边作等边三角形,得到第一个等边三角形AB
1C
1,再以等边三角形AB
1C
1的B
1C
1边上的高AB
2为边作等边三角形,得到第二个等边三角形AB
2C
2,再以等边三角形AB
2C
2的边B
2C
2边上的高AB
3为边作等边三角形,得到第三个等边AB
3C
3;…,如此下去,这样得到的第n个等边三角形AB
nC
n的面积为
.
查看答案和解析>>
科目:czsx
来源:2013年初中毕业升学考试(黑龙江龙东地区卷)数学(解析版)
题型:填空题
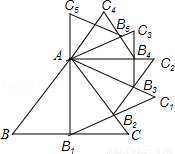
已知等边三角形ABC的边长是2,以BC边上的高AB1为边作等边三角形,得到第一个等边三角形AB1C1,再以等边三角形AB1C1的B1C1边上的高AB2为边作等边三角形,得到第二个等边三角形AB2C2,再以等边三角形AB2C2的边B2C2边上的高AB3为边作等边三角形,得到第三个等边AB3C3;…,如此下去,这样得到的第n个等边三角形ABnCn的面积为 .
查看答案和解析>>
科目:czsx
来源:2010年贵州省黔南州中考数学试卷(解析版)
题型:选择题
(2010•黔南州)如图,已知等边三角形ABC的边长为2,DE是它的中位线,则下面四个结论:
(1)DE=1;
(2)AB边上的高为

;
(3)△CDE∽△CAB;
(4)△CDE的面积与△CAB面积之比为1:4.
其中正确的有( )

A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:czsx
来源:2009年上海市周浦中学初中毕业生升学文化课模拟考试(解析版)
题型:选择题
(2010•黔南州)如图,已知等边三角形ABC的边长为2,DE是它的中位线,则下面四个结论:
(1)DE=1;
(2)AB边上的高为

;
(3)△CDE∽△CAB;
(4)△CDE的面积与△CAB面积之比为1:4.
其中正确的有( )

A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:czsx
来源:第24章《相似形》中考题集(07):24.3 相似三角形的性质(解析版)
题型:选择题
如图,已知等边三角形ABC的边长为2,DE是它的中位线,则下面四个结论:
(1)DE=1;
(2)AB边上的高为

;
(3)△CDE∽△CAB;
(4)△CDE的面积与△CAB面积之比为1:4.
其中正确的有( )

A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:czsx
来源:《第27章 相似》2010年同步学习检测(二)(解析版)
题型:选择题
如图,已知等边三角形ABC的边长为2,DE是它的中位线,则下面四个结论:
(1)DE=1;
(2)AB边上的高为

;
(3)△CDE∽△CAB;
(4)△CDE的面积与△CAB面积之比为1:4.
其中正确的有( )

A.1个
B.2个
C.3个
D.4个
查看答案和解析>>







 如图所示,已知O为正三角形ABC的高AD、BE、CF的交点,P是△ABC所在平面上的任一点,作PL⊥AD于L,PM⊥BE于M,PN⊥CF于N.试证:PL、PM、PN中较大的一条线段等于其它两条线段的和.
如图所示,已知O为正三角形ABC的高AD、BE、CF的交点,P是△ABC所在平面上的任一点,作PL⊥AD于L,PM⊥BE于M,PN⊥CF于N.试证:PL、PM、PN中较大的一条线段等于其它两条线段的和. 如图所示,已知O为正三角形ABC的高AD、BE、CF的交点,P是△ABC所在平面上的任一点,作PL⊥AD于L,PM⊥BE于M,PN⊥CF于N.试证:PL、PM、PN中较大的一条线段等于其它两条线段的和.
如图所示,已知O为正三角形ABC的高AD、BE、CF的交点,P是△ABC所在平面上的任一点,作PL⊥AD于L,PM⊥BE于M,PN⊥CF于N.试证:PL、PM、PN中较大的一条线段等于其它两条线段的和.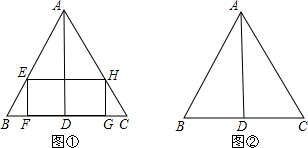
 如图,已知等边三角形ABC的边长为2,DE是它的中位线,则下面四个结论:
如图,已知等边三角形ABC的边长为2,DE是它的中位线,则下面四个结论: (2013•黑龙江)已知等边三角形ABC的边长是2,以BC边上的高AB1为边作等边三角形,得到第一个等边三角形AB1C1,再以等边三角形AB1C1的B1C1边上的高AB2为边作等边三角形,得到第二个等边三角形AB2C2,再以等边三角形AB2C2的边B2C2边上的高AB3为边作等边三角形,得到第三个等边AB3C3;…,如此下去,这样得到的第n个等边三角形ABnCn的面积为
(2013•黑龙江)已知等边三角形ABC的边长是2,以BC边上的高AB1为边作等边三角形,得到第一个等边三角形AB1C1,再以等边三角形AB1C1的B1C1边上的高AB2为边作等边三角形,得到第二个等边三角形AB2C2,再以等边三角形AB2C2的边B2C2边上的高AB3为边作等边三角形,得到第三个等边AB3C3;…,如此下去,这样得到的第n个等边三角形ABnCn的面积为
 ;
;
 ;
;
 ;
;
 ;
;