精英家教网 >
试题搜索列表 >如图,在平面直角坐标系中,将直角三角形的直角顶点放在P(4,4)处,两直角边与坐标轴交于点A和点B
如图,在平面直角坐标系中,将直角三角形的直角顶点放在P(4,4)处,两直角边与坐标轴交于点A和点B答案解析
科目:czsx
来源:
题型:
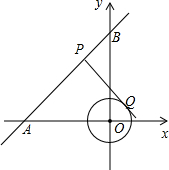
(2012•镇江)如图,在平面直角坐标系xOy中,直线AB经过点A(-4,0)、B(0,4),⊙O的半径为1(O为坐标原点),点P在直线AB上,过点P作⊙O的一条切线PQ,Q为切点,则切线长PQ的最小值为
.
查看答案和解析>>
科目:czsx
来源:
题型:
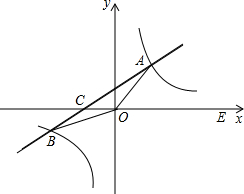
(2013•巴中)如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数y=
的图象交于一、三象限内的A、B两点,直线AB与x轴交于点C,点B的坐标为(-6,n),线段OA=5,E为x轴正半轴上一点,且tan∠AOE=
(1)求反比例函数的解析式;
(2)求△AOB的面积.
查看答案和解析>>
科目:czsx
来源:
题型:
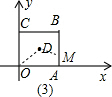
如图,在平面直角坐标系中,正方形OABC的面积是16.
(1)求正方形OABC的对角线的交点D的坐标;
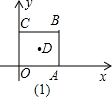
(2)直线y=2x+8交x轴于E,交y轴于F,它沿x轴正方向以每秒移动1个单位长度的速度平移,设平移的时间为t秒,问是否存在t的
值,使直线EF平分正方形OABC的面积?若存在,请求出t的值;若不存在,请说明理由;
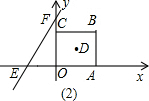
(3)如图,点P为正方形OABC的对角线AC上的动点(端点A、C除外),PM⊥PO,交直线AB于M,给出下列两个结论:①
的值不变;②
的值不变;其中有且只有一个结论是正确的,请你选出正确的结论,予以证明并求其值.
查看答案和解析>>
科目:czsx
来源:
题型:
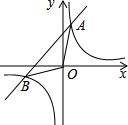
如图,在平面直角坐标系xOy中,反比例函数y=
的图象与直线y=ax+2的图象交于点A(m,3),
(1)试确定a的值.
(2)若反比例函数的图象y=
与直线y=ax+2另一个交点为B,求△AOB的面积.
查看答案和解析>>
科目:czsx
来源:
题型:

(2013•宝应县模拟)如图,在平面直角坐标系中,一次函数y=
-x+8的图象与x轴,y轴交于A、B两点,OD=
OB,AC=
AB,过点C作CE⊥OA于点E,点M从点C出发,沿CD方向运动,过点M作MN⊥OA于点N,过点N作NP∥AB,交OB于点P,当点N与点O重合时点M停止运动.设AN=a.
(1)求点C的坐标;
(2)用含a的代数式表示NP;
(3)是否存在点M,使△MNP为等腰三角形?若存在,请求出所有满足要求的a的值;若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:

(2013•平遥县模拟)如图,在平面直角坐标系中,将一块等腰直角三角板ABC放在第二象限,斜靠在两坐标轴上,点C坐标为(-1,0),tan∠ACO=2.一次函数y=kx+b的图象经过点B、C,反比例函数y=
的图象经过点B.
(1)求一次函数和反比例函数的关系式;
(2)直接写出当x<0时,kx+b-
<0的解集;
(3)在x轴上找一点M,使得AM+BM的值最小,并求出点M的坐标和AM+BM的最小值.
查看答案和解析>>
科目:czsx
来源:
题型:

如图,在平面直角坐标系中,四边形OABC是梯形,OA∥BC,点A的坐标为(6,0),点B的坐标为(3,4),点C在y轴的正半轴上.动点M在OA上运动,从O点出发到A点;动点N在AB上运动,从A点出发到B点.两个动点同时出发,速度都是每秒1个单位长度,当其中一个点到达终点时,另一个点也随即停止,设两个点的运动时间为t(秒).
(1)求线段AB的长;当t为何值时,MN∥OC;
(2)设△CMN的面积为S,求S与t之间的函数解析式,并指出自变量t的取值范围;S是否有最小值?若有最小值,最小值是多少?
(3)连接AC,那么是否存在这样的t,使MN与AC互相垂直?若存在,求出这时的t值;若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
如图,在平面直角坐标系中,一抛物线的对称轴为直线x=1,与y轴负半轴交
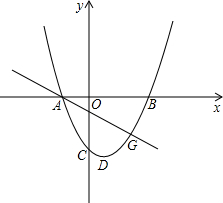
于C点,与x轴交于A、B两点,其中B点的坐标为(3,0),C点坐标为(0,-3).
(1)求此抛物线的解析式;
(2)若点G(2,-3)是该抛物线上一点,点E是直线AG下方的抛物线上一动点,当点E运动到什么位置时,△AEG的面积最大?求出此时E点的坐标和△AEG的最大面积;
(3)若平行于x轴的直线与该抛物线交于M、N两点(其中点M在点N的右侧),在x轴上是否存在点Q,使△MNQ为等腰直角三角形?若存在,请求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
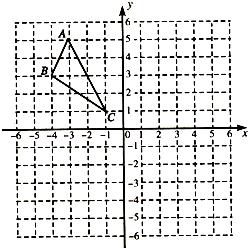
22、如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(-3,5),B(-4,3),C(-1,1).
(1)作出△ABC向右平移5个单位的△A
1B
1C
1;
(2)作出△ABC关于y轴对称的△A
2B
2C
2,并写出点C
2的坐标.
查看答案和解析>>
科目:czsx
来源:
题型:
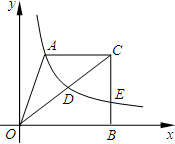
(2013•江北区模拟)如图,在平面直角坐标系中,梯形AOBC的边OB在x轴的正半轴上,AC∥OB,BC⊥OB,过点A的双曲线y=
的一支在第一象限交梯形对角线OC于点D,交边BC于点E.若
=
,S
△OAC=2,则k的值为
.
查看答案和解析>>
科目:czsx
来源:
题型:
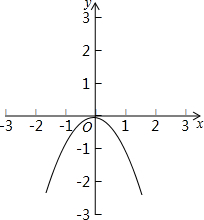
(2007•海淀区一模)已知,如图,在平面直角坐标系xOy中,抛物线l
1的解析式为y=-x
2,将抛物线l
1平移后得到抛物线l
2,若抛物线l
2经过点(0,2),且其顶点A的横坐标为最小正整数.
(1)求抛物线l
2的解析式;
(2)说明将抛物线l
1如何平移得到抛物线l
2;
(3)若将抛物线l
2沿其对称轴继续上下平移,得到抛物线l
3,设抛物线l
3的顶点为B,直线OB与抛物线l
3的另一个交点为C.当OB=OC时,求点C的坐标.
查看答案和解析>>
科目:czsx
来源:
题型:
如图,在平面直角坐标系中,抛物线与x轴交于A、B两点(A在B的左侧),与y轴交于点C(0,4),顶点为(1,
).
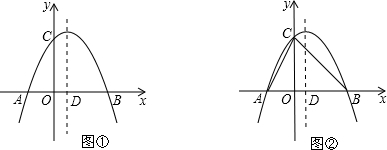
(1)求抛物线的函数关系式;
(2)如图①,设该抛物线的对称轴与x轴交于点D,试在对称轴上找出点P,使△CDP为等腰三角形,请直接写出满足条件的所有点P的坐标;
(3)如图②,连结AC、BC,若点E是线段AB上的一个动点(与点A、B不重合),过点E作EF∥AC交线段BC于点F,连结CE,记△CEF的面积为S,求出S的最大值及此时E点的坐标.
查看答案和解析>>
科目:czsx
来源:
题型:

如图,在平面直角坐标系中,直线y=-2x+2与x轴y轴分别相交于点A,B,四边形ABCD是正方形,曲线
y=在第一象限经过点D.
(1)求正方形ABCD的面积;
(2)求双曲线的函数解析式.
查看答案和解析>>
科目:czsx
来源:
题型:
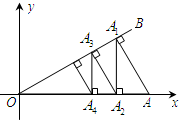
(2013•平遥县模拟)如图,在平面直角坐标系中,∠AOB=30°,点A坐标为(2,0).过A作AA
1⊥OB,垂足为A
1;过A
1作A
1A
2⊥x轴,垂足为A
2;再过点A
2作A
2A
3⊥OB,垂足为点A
3;再过点A
3作A
3A
4⊥x轴,垂足为A
4…;这样一直作下去,则A
2013的纵坐标为
.
查看答案和解析>>
科目:czsx
来源:
题型:
如图,在平面直角坐标系中,O为坐标原点,⊙C的圆心坐标为(-2,-2),半径为
.函数y=-x+2的图象与x轴交于点A,与y轴交于点B,点P为线段AB上一动点.
(1)连接CO,求证:CO⊥AB;
(2)若△POA是等腰三角形,求点P的坐标;
(3)当直线PO与⊙C相切时,求∠POA的度数;当直线PO与⊙C相交时,设交点
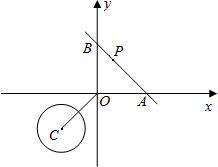
为E、F,点M为线段EF的中点,令PO=t,MO=s,求s与t之间的函数关系,并写出t的取值范围.
查看答案和解析>>
科目:czsx
来源:
题型:
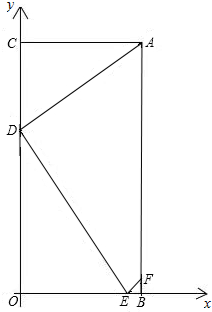
如图:在平面直角坐标系中,矩形ABCD的顶点A的坐标为(4,8),D是OC上一点,且CD:OD=3:5,连接AD,过D点作DE⊥AD交OB于E,过E作EF∥AD,交AB于F
(1)求经过A、D两点的直线解析式;
(2)求EF的长.
查看答案和解析>>
科目:czsx
来源:
题型:
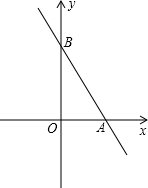
已知:如图,在平面直角坐标系xOy中,一次函数y=-2x+4的图象分别与x、y轴交于点A、B,点P在x轴上,若S
△ABP=6,求直线PB的函数解析式.
查看答案和解析>>
科目:czsx
来源:
题型:
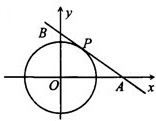
18、如图,在平面直角坐标系中,以坐标原点O为圆心,2为半径画⊙O,P是⊙O是一动点且P在第一象限内,过P作⊙O切线与x轴相交于点A,与y轴相交于点B.则线段AB的最小值是
4.
.
查看答案和解析>>
科目:czsx
来源:
题型:
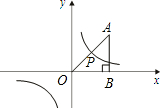
如图,在平面直角坐标系中,Rt△AOB的面积是4,双曲线
y=的图象过斜边OA的中点P,则k等于( )
查看答案和解析>>
科目:czsx
来源:
题型:
如图,在平面直角坐标系中,点A是动点且纵坐标为4,点B是线段OA上的一个动点,过点B作直线MN平行于x轴,设MN分别交射线OA与x轴所成的两个角的平分线于点E、F.
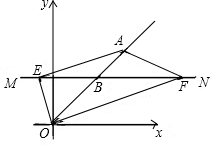
(1)求证:EB=BF;
(2)当
为何值时,四边形AEOF是矩形?证明你的结论;
(3)是否存在点A、B,使四边形AEOF为正方形?若存在,求点A与B的坐标;若不存在,说明理由.
查看答案和解析>>

 (2012•镇江)如图,在平面直角坐标系xOy中,直线AB经过点A(-4,0)、B(0,4),⊙O的半径为1(O为坐标原点),点P在直线AB上,过点P作⊙O的一条切线PQ,Q为切点,则切线长PQ的最小值为
(2012•镇江)如图,在平面直角坐标系xOy中,直线AB经过点A(-4,0)、B(0,4),⊙O的半径为1(O为坐标原点),点P在直线AB上,过点P作⊙O的一条切线PQ,Q为切点,则切线长PQ的最小值为 (2013•巴中)如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数y=
(2013•巴中)如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数y=


 如图,在平面直角坐标系xOy中,反比例函数y=
如图,在平面直角坐标系xOy中,反比例函数y= (2013•宝应县模拟)如图,在平面直角坐标系中,一次函数y=-
(2013•宝应县模拟)如图,在平面直角坐标系中,一次函数y=- (2013•平遥县模拟)如图,在平面直角坐标系中,将一块等腰直角三角板ABC放在第二象限,斜靠在两坐标轴上,点C坐标为(-1,0),tan∠ACO=2.一次函数y=kx+b的图象经过点B、C,反比例函数y=
(2013•平遥县模拟)如图,在平面直角坐标系中,将一块等腰直角三角板ABC放在第二象限,斜靠在两坐标轴上,点C坐标为(-1,0),tan∠ACO=2.一次函数y=kx+b的图象经过点B、C,反比例函数y= 如图,在平面直角坐标系中,四边形OABC是梯形,OA∥BC,点A的坐标为(6,0),点B的坐标为(3,4),点C在y轴的正半轴上.动点M在OA上运动,从O点出发到A点;动点N在AB上运动,从A点出发到B点.两个动点同时出发,速度都是每秒1个单位长度,当其中一个点到达终点时,另一个点也随即停止,设两个点的运动时间为t(秒).
如图,在平面直角坐标系中,四边形OABC是梯形,OA∥BC,点A的坐标为(6,0),点B的坐标为(3,4),点C在y轴的正半轴上.动点M在OA上运动,从O点出发到A点;动点N在AB上运动,从A点出发到B点.两个动点同时出发,速度都是每秒1个单位长度,当其中一个点到达终点时,另一个点也随即停止,设两个点的运动时间为t(秒). 于C点,与x轴交于A、B两点,其中B点的坐标为(3,0),C点坐标为(0,-3).
于C点,与x轴交于A、B两点,其中B点的坐标为(3,0),C点坐标为(0,-3). 22、如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(-3,5),B(-4,3),C(-1,1).
22、如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(-3,5),B(-4,3),C(-1,1). (2013•江北区模拟)如图,在平面直角坐标系中,梯形AOBC的边OB在x轴的正半轴上,AC∥OB,BC⊥OB,过点A的双曲线y=
(2013•江北区模拟)如图,在平面直角坐标系中,梯形AOBC的边OB在x轴的正半轴上,AC∥OB,BC⊥OB,过点A的双曲线y=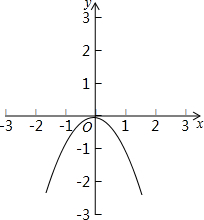 (2007•海淀区一模)已知,如图,在平面直角坐标系xOy中,抛物线l1的解析式为y=-x2,将抛物线l1平移后得到抛物线l2,若抛物线l2经过点(0,2),且其顶点A的横坐标为最小正整数.
(2007•海淀区一模)已知,如图,在平面直角坐标系xOy中,抛物线l1的解析式为y=-x2,将抛物线l1平移后得到抛物线l2,若抛物线l2经过点(0,2),且其顶点A的横坐标为最小正整数.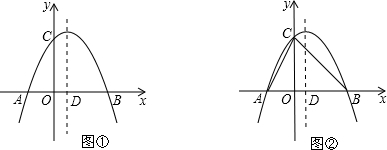
 如图,在平面直角坐标系中,直线y=-2x+2与x轴y轴分别相交于点A,B,四边形ABCD是正方形,曲线y=
如图,在平面直角坐标系中,直线y=-2x+2与x轴y轴分别相交于点A,B,四边形ABCD是正方形,曲线y= (2013•平遥县模拟)如图,在平面直角坐标系中,∠AOB=30°,点A坐标为(2,0).过A作AA1⊥OB,垂足为A1;过A1作A1A2⊥x轴,垂足为A2;再过点A2作A2A3⊥OB,垂足为点A3;再过点A3作A3A4⊥x轴,垂足为A4…;这样一直作下去,则A2013的纵坐标为
(2013•平遥县模拟)如图,在平面直角坐标系中,∠AOB=30°,点A坐标为(2,0).过A作AA1⊥OB,垂足为A1;过A1作A1A2⊥x轴,垂足为A2;再过点A2作A2A3⊥OB,垂足为点A3;再过点A3作A3A4⊥x轴,垂足为A4…;这样一直作下去,则A2013的纵坐标为 为E、F,点M为线段EF的中点,令PO=t,MO=s,求s与t之间的函数关系,并写出t的取值范围.
为E、F,点M为线段EF的中点,令PO=t,MO=s,求s与t之间的函数关系,并写出t的取值范围.  如图:在平面直角坐标系中,矩形ABCD的顶点A的坐标为(4,8),D是OC上一点,且CD:OD=3:5,连接AD,过D点作DE⊥AD交OB于E,过E作EF∥AD,交AB于F
如图:在平面直角坐标系中,矩形ABCD的顶点A的坐标为(4,8),D是OC上一点,且CD:OD=3:5,连接AD,过D点作DE⊥AD交OB于E,过E作EF∥AD,交AB于F 已知:如图,在平面直角坐标系xOy中,一次函数y=-2x+4的图象分别与x、y轴交于点A、B,点P在x轴上,若S△ABP=6,求直线PB的函数解析式.
已知:如图,在平面直角坐标系xOy中,一次函数y=-2x+4的图象分别与x、y轴交于点A、B,点P在x轴上,若S△ABP=6,求直线PB的函数解析式.  18、如图,在平面直角坐标系中,以坐标原点O为圆心,2为半径画⊙O,P是⊙O是一动点且P在第一象限内,过P作⊙O切线与x轴相交于点A,与y轴相交于点B.则线段AB的最小值是
18、如图,在平面直角坐标系中,以坐标原点O为圆心,2为半径画⊙O,P是⊙O是一动点且P在第一象限内,过P作⊙O切线与x轴相交于点A,与y轴相交于点B.则线段AB的最小值是
 (1)求证:EB=BF;
(1)求证:EB=BF;