科目：czsx 来源： 题型：
探究问题
(1)阅读理解：
①如图1，在△ABC所在平面上存在一点P，使它到三角形三顶点的距离之和最小，则称点P为△ABC的费马点，此时PA＋PB＋PC的值为△ABC的费马距离．
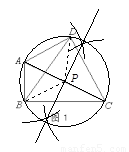
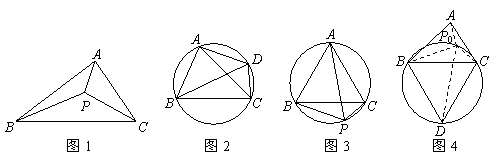②如图2，若四边形ABCD的四个顶点在同一个圆上，则有AB·CD＋BC·AD＝AC·BD．此为托勒密定理．
(2)知识迁移：
①请你利用托勒密定理，解决如下问题：
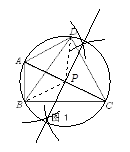
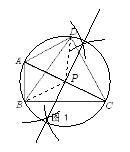
如图3，已知点P为等边△ABC外接圆的弧BC上任意一点．求证：PB＋PC＝PA．
②根据(2)①的结论，我们有如下探寻△ABC(其中∠A、∠B、∠C均小于120º)的费马点和费马距离的方法：
第一步：如图4，在△ABC的外部以BC为边长作等边△BCD及其外接圆；
第二步：在弧BC上取一点P0，连接P0A、P0B、P0C、P0D．
易知P0A＋P0B＋P0C＝P0A＋(P0B＋P0C)＝P0A＋ ；
第三步：请你根据(1)①中定义，在图4中找出△ABC的费马点P，线段 的长度即为△ABC的费马距离．
(3)知识应用：
2010年4月，我国西南地区出现了罕见的持续干旱现象，许多村庄出现了人、畜饮水困难．为解决老百姓饮水问题，解放军某部到云南某地打井取水．
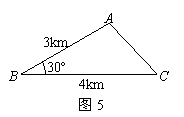已知三村庄A、B、C构成了如图5所示的△ABC(其中∠A、∠B、∠C均小于120º)，现选取一点P打水井，使水井P到三村庄A、B、C所铺设的输水管总长度最小．求输水管总长度的最小值．
科目：czsx 来源： 题型：
| 2 |
科目：czsx 来源： 题型：
定义：只有一组对角是直角的四边形叫做损矩形，连结它的两个非直角顶点的线段叫做这个损矩形的直径.
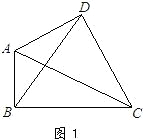
1.如图1，损矩形ABCD，∠ABC=∠ADC=90°，则该损矩形的直径是线段 .
2.在线段AC上确定一点P，使损矩形的四个顶点都在以P为圆心的同一圆上(即损矩形的四个顶点在同一个圆上)，请作出这个圆，并说明你的理由. 友情提醒：“尺规作图”不要求写作法，但要保留作图痕迹．
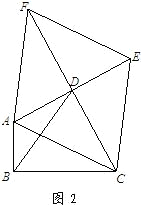
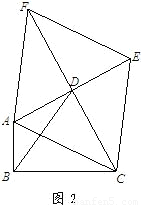
3.如图2，△ABC中，∠ABC＝90°，以AC为一边向形外作菱形ACEF，D为菱形ACEF的中心，连结BD，当BD平分∠ABC时，判断四边形ACEF为何种特殊的四边形？请说明理由. 若此时AB＝3，BD＝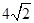
，求BC的长.
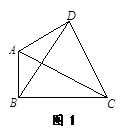
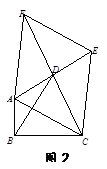
科目：czsx 来源：2012-2013学年江苏扬州江都区麾村中学九年级上学期期中考试数学试卷（解析版） 题型：解答题
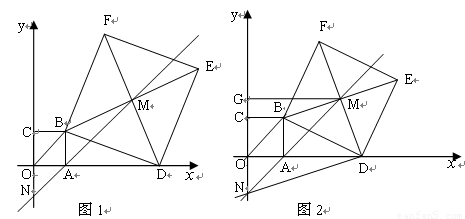
如图1，在直角坐标系中，点A的坐标为(1，0)，以OA为边在第一象限内作正方形OABC，点D是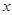
轴正半轴上一动点（OD＞1）,连结BD，以BD为边在第一象限内作正方形DBFE，设M为正方形DBFE的中心，直线MA交
轴于点N．如果定义：只有一组对角是直角的四边形叫做损矩形．
（1）试找出图1中的一个损矩形；
（2）试说明(1)中找出的损矩形的四个顶点在同一个圆上；
（3）随着点D位置的变化，点N的位置是否会发生变化？若没有发生变化，求出点N的坐标；若发生变化，请说明理由；
（4）在图2中，过点M作MG⊥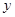轴于点G，连结DN，若四边形DMGN为损矩形，求D点坐标．
科目：czsx 来源：2011-2012学年江苏省泰兴市黄桥区九年级中考一模数学试卷（解析版） 题型：解答题
定义：只有一组对角是直角的四边形叫做损矩形，连结它的两个非直角顶点的线段叫做这个损矩形的直径.
1.如图1，损矩形ABCD，∠ABC=∠ADC=90°，则该损矩形的直径是线段 .
2.在线段AC上确定一点P，使损矩形的四个顶点都在以P为圆心的同一圆上(即损矩形的四个顶点在同一个圆上)，请作出这个圆，并说明你的理由. 友情提醒：“尺规作图”不要求写作法，但要保留作图痕迹．
3.如图2，△ABC中，∠ABC＝90°，以AC为一边向形外作菱形ACEF，D为菱形ACEF的中心，连结BD，当BD平分∠ABC时，判断四边形ACEF为何种特殊的四边形？请说明理由. 若此时AB＝3，BD＝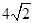
，求BC的长.
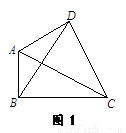
科目：czsx 来源： 题型：
，求BC的长.
科目：czsx 来源：2012届江苏省泰兴市黄桥区九年级中考一模数学试卷（带解析） 题型：解答题
定义：只有一组对角是直角的四边形叫做损矩形，连结它的两个非直角顶点的线段叫做这个损矩形的直径.
【小题1】如图1，损矩形ABCD，∠ABC=∠ADC=90°，则该损矩形的直径是线段 .
【小题2】在线段AC上确定一点P，使损矩形的四个顶点都在以P为圆心的同一圆上(即损矩形的四个顶点在同一个圆上)，请作出这个圆，并说明你的理由. 友情提醒：“尺规作图”不要求写作法，但要保留作图痕迹．
【小题3】如图2，△ABC中，∠ABC＝90°，以AC为一边向形外作菱形ACEF，D为菱形ACEF的中心，连结BD，当BD平分∠ABC时，判断四边形ACEF为何种特殊的四边形？请说明理由. 若此时AB＝3，BD＝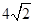
，求BC的长.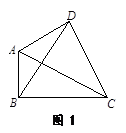
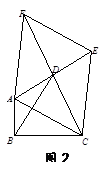
科目：czsx 来源：2013届江苏扬州江都区麾村中学九年级上学期期中考试数学试卷（带解析） 题型：解答题
如图1，在直角坐标系中，点A的坐标为(1，0)，以OA为边在第一象限内作正方形OABC，点D是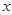
轴正半轴上一动点（OD＞1）,连结BD，以BD为边在第一象限内作正方形DBFE，设M为正方形DBFE的中心，直线MA交
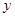轴于点N．如果定义：只有一组对角是直角的四边形叫做损矩形．
（1）试找出图1中的一个损矩形；
（2）试说明(1)中找出的损矩形的四个顶点在同一个圆上；
（3）随着点D位置的变化，点N的位置是否会发生变化？若没有发生变化，求出点N的坐标；若发生变化，请说明理由；
（4）在图2中，过点M作MG⊥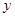轴于点G，连结DN，若四边形DMGN为损矩形，求D点坐标．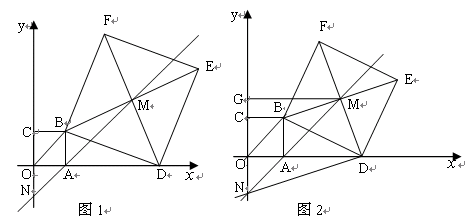 
科目：czsx 来源： 题型：
定义：只有一组对角是直角的四边形叫做损矩形，连结它的两个非直角顶点的线段叫做这个损矩形的直径.
⑴如图1，损矩形ABCD，∠ABC=∠ADC=90°，则该损矩形的直径是线段 .
⑵在线段AC上确定一点P，使损矩形的四个顶点都在以P为圆心的同一圆上(即损矩形的四个顶点在同一个圆上)，请作出这个圆，并说明你的理由. 友情提醒：“尺规作图”不要求写作法，但要保留作图痕迹．
⑶如图2，△ABC中，∠ABC＝90°，以AC为一边向形外作菱形ACEF，D为菱形ACEF的中心，连结BD，当BD平分∠ABC时，判断四边形ACEF为何种特殊的四边形？请说明理由. 若此时AB＝3，BD＝
，求BC的长.
 |
科目：czsx 来源：2011-2012学年江苏省南京市旭东中学九年级（上）月考数学试卷（10月份）（解析版） 题型：解答题
，求BC的长．
科目：czsx 来源：2009年江苏省无锡市中考数学模拟卷（解析版） 题型：解答题
，求BC的长．
科目：czsx 来源：江苏省无锡市天一实验学校2012届九年级一模数学试题 题型：044
定义：只有一组对角是直角的四边形叫做损矩形，连结它的两个非直角顶点的线段叫做这个损矩形的直径．
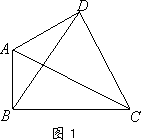
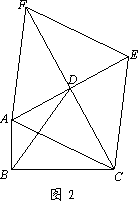
(1)如图1，损矩形ABCD，∠ABC＝∠ADC＝90°，则该损矩形的直径是线段________．
(2)在线段AC上确定一点P，使损矩形的四个顶点都在以P为圆心的同一圆上(即损矩形的四个顶点在同一个圆上)，请作出这个圆，并说明你的理由．友情提醒：“尺规作图”不要求写作法，但要保留作图痕迹．
(3)如图2，，△ABC中，∠ABC＝90°，以AC为一边向形外作菱形ACEF，D为菱形ACEF的中心，连结BD，当BD平分∠ABC时，判断四边形ACEF为何种特殊的四边形？请说明理由．若此时AB＝3，BD＝
，求BC的长．
科目：czsx 来源：2012年江苏省泰州市泰兴市黄桥区中考数学一模试卷（解析版） 题型：解答题
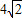，求BC的长．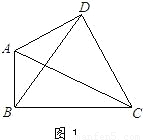
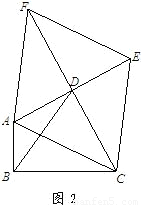
科目：czsx 来源：2013年陕西省中考数学模拟试卷（四）（解析版） 题型：解答题
，求BC的长．
科目：czsx 来源：2012年江苏省无锡市蠡园中学中考适应性练习数学试卷（二）（解析版） 题型：解答题
，求BC的长．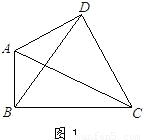
科目：czsx 来源：2012年江苏省无锡市天一实验学校中考数学一模试卷（解析版） 题型：解答题
，求BC的长．
科目：czsx 来源：2011年中考复习五校第二次模拟考试数学试卷（解析版） 题型：解答题
，求BC的长．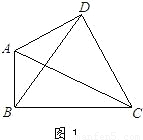
科目：czsx 来源：江苏省泰兴市黄桥区2012届九年级中考一模数学试题 题型：044
定义：只有一组对角是直角的四边形叫做损矩形，连结它的两个非直角顶点的线段叫做这个损矩形的直径．
(1)如图，损矩形ABCD，∠ABC＝∠ADC＝90°，则该损矩形的直径是线段________．
(2)在线段AC上确定一点P，使损矩形的四个顶点都在以P为圆心的同一圆上(即损矩形的四个顶点在同一个圆上)，请作出这个圆，并说明你的理由． 友情提醒：“尺规作图”不要求写作法，但要保留作图痕迹．
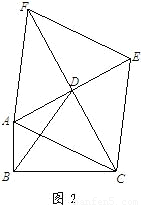
(3)如图，△ABC中，∠ABC＝90°，以AC为一边向形外作菱形ACEF，D为菱形ACEF的中心，连结BD，当BD平分∠ABC时，判断四边形ACEF为何种特殊的四边形？请说明理由．若此时AB＝3，BD＝
，求BC的长．
科目：czsx 来源： 题型：044
(1)大家知道：四个点不能确定一个圆，但是有些特殊四边形的四个顶点在同一个圆上．请说出这些特殊的四边形，并研究这些四边形的四个内角之间有什么特殊的大小关系．
(2)画一个圆，再在这个圆上任取四个点A、B、C、D，连接AB、BC、CD、DA，分别度量∠A、∠B、∠C、∠D的大小，你发现这四个角的度数之间又有怎样的关系?
(3)根据(1)(2)两题的结论，试猜想：一个四边形的四个角具有怎样的大小关系时，这个四边形的四个顶点在同一圆上?
科目：czsx 来源： 题型：