
科目:czsx 来源:2012-2013学年浙江杭州萧山党湾初级中学八年级10月月考数学试卷(解析版) 题型:解答题
画图题
①已知线段m和n,请用直尺和圆规作出等腰△ABC,使得AB=AC, BC=m,∠A的平分线等于n.(只保留作图痕迹,不写做法)
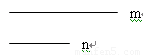
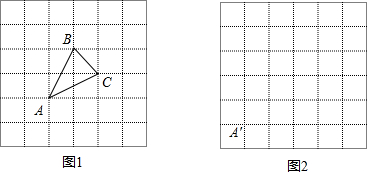
②如图,在 方格中画出所有以AB为一边的等腰Rt△ABC。(要求点C也在格点上)
方格中画出所有以AB为一边的等腰Rt△ABC。(要求点C也在格点上)
科目:czsx 来源:2012-2013学年浙江杭州萧山党湾初级中学八年级10月月考数学试卷(带解析) 题型:解答题
画图题
①已知线段m和n,请用直尺和圆规作出等腰△ABC,使得AB=AC, BC=m,∠A的平分线等于n.(只保留作图痕迹,不写做法)
②如图,在 方格中画出所有以AB为一边的等腰Rt△ABC。(要求点C也在格点上)
方格中画出所有以AB为一边的等腰Rt△ABC。(要求点C也在格点上)
科目:czsx 来源: 题型:
 24、如图,在△ABC中,D是BC的中点,E是AD的中点,过点A作AF∥BC,AF与CE的延长线相交于点F,连接BF.
24、如图,在△ABC中,D是BC的中点,E是AD的中点,过点A作AF∥BC,AF与CE的延长线相交于点F,连接BF.科目:czsx 来源: 题型:
科目:czsx 来源: 题型:
 23、如图所示,在△ABC中,AD⊥BC于点D,E,F分别是AB,AC边的中点,连接DE,EF,FD,当△ABC满足条件
23、如图所示,在△ABC中,AD⊥BC于点D,E,F分别是AB,AC边的中点,连接DE,EF,FD,当△ABC满足条件科目:czsx 来源: 题型:阅读理解
| 5 |
| 2 |
| 22+12 |
| 5 |
| 12+12 |
| 2 |
| 10 |
科目:czsx 来源: 题型:
 9、如图,已知线段a,h作等腰△ABC,使AB=AC,且BC=a,BC边上的高AD=h.张红的作法是:
9、如图,已知线段a,h作等腰△ABC,使AB=AC,且BC=a,BC边上的高AD=h.张红的作法是:科目:czsx 来源: 题型:
 (2013•集美区一模)如图,在△ABC中,D、E分别是边AB、AC的中点,F为CA延长线上一点,∠F=∠C.
(2013•集美区一模)如图,在△ABC中,D、E分别是边AB、AC的中点,F为CA延长线上一点,∠F=∠C.科目:czsx 来源: 题型:
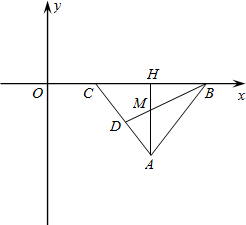 如图,在直角坐标系xOy中,点A的坐标为(12,-8),点B、C在x轴上,tan∠ABC=
如图,在直角坐标系xOy中,点A的坐标为(12,-8),点B、C在x轴上,tan∠ABC=| 4 | 3 |
科目:czsx 来源:2006年湖南省益阳市中考数学试卷(解析版) 题型:选择题

科目:czsx 来源:第24章《相似形》中考题集(20):24.3 相似三角形的性质(解析版) 题型:解答题
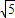 ,BC=
,BC= ;
; ,BC=
,BC=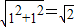 ,于是画出线段AB、AC、BC,从而画出格点△ABC.
,于是画出线段AB、AC、BC,从而画出格点△ABC. .(直接画出图形,不写过程);
.(直接画出图形,不写过程);
科目:czsx 来源:2011年云南省昭通市昭阳区二中中考数学模拟试卷(三)(解析版) 题型:解答题
 ,BC=
,BC= ;
;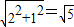 ,BC=
,BC= ,于是画出线段AB、AC、BC,从而画出格点△ABC.
,于是画出线段AB、AC、BC,从而画出格点△ABC. .(直接画出图形,不写过程);
.(直接画出图形,不写过程);
科目:czsx 来源:2010年江苏省连云港市中考数学二模试卷(解析版) 题型:解答题
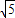 ,BC=
,BC=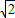 ;
;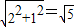 ,BC=
,BC=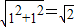 ,于是画出线段AB、AC、BC,从而画出格点△ABC.
,于是画出线段AB、AC、BC,从而画出格点△ABC.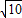 .(直接画出图形,不写过程);
.(直接画出图形,不写过程);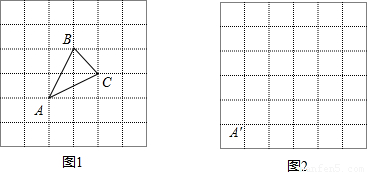
科目:czsx 来源:2013年云南省黔西南州册亨县中考数学模拟试卷(解析版) 题型:解答题
 ,BC=
,BC= ;
; ,BC=
,BC=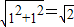 ,于是画出线段AB、AC、BC,从而画出格点△ABC.
,于是画出线段AB、AC、BC,从而画出格点△ABC. .(直接画出图形,不写过程);
.(直接画出图形,不写过程);
科目:czsx 来源:2012年上海市中考数学模拟试卷(一)(解析版) 题型:解答题
 ,BC=
,BC= ;
; ,BC=
,BC=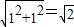 ,于是画出线段AB、AC、BC,从而画出格点△ABC.
,于是画出线段AB、AC、BC,从而画出格点△ABC. .(直接画出图形,不写过程);
.(直接画出图形,不写过程);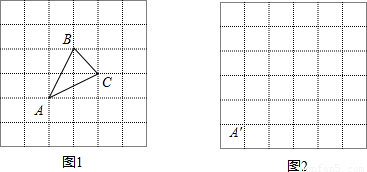
科目:czsx 来源: 题型:解答题
 点F,连接BF.
点F,连接BF.科目:czsx 来源:2012年江苏省南京市雨花台区中考数学一模试卷(解析版) 题型:解答题
 ,BC=
,BC= ;
; ,BC=
,BC= ,于是画出线段AB、AC、BC,从而画出格点△ABC.
,于是画出线段AB、AC、BC,从而画出格点△ABC. .(直接画出图形,不写过程);
.(直接画出图形,不写过程);
科目:czsx 来源:第24章《图形的相似》中考题集(17):24.3 相似三角形(解析版) 题型:解答题
 ,BC=
,BC= ;
; ,BC=
,BC= ,于是画出线段AB、AC、BC,从而画出格点△ABC.
,于是画出线段AB、AC、BC,从而画出格点△ABC. .(直接画出图形,不写过程);
.(直接画出图形,不写过程);