精英家教网 >
试题搜索列表 >初三数学人教版y=-4\1(x+2)的平方和y=-4\1(x-1)的平方在同一直角坐标系中描点画出下列二次函数的图像的出
初三数学人教版y=-4\1(x+2)的平方和y=-4\1(x-1)的平方在同一直角坐标系中描点画出下列二次函数的图像的出答案解析
科目:czsx
来源:
题型:044
为了了解一次初三数学竞赛成绩,从3000名学生的成绩中抽取得部分中有1人得100分,2人得95分,8人得90分,10人得80分,15人得70分.
(1)指出这个问题中的总体、个体、样本和样本容量.
(2)求样本的平均数.
查看答案和解析>>
科目:czsx
来源:
题型:
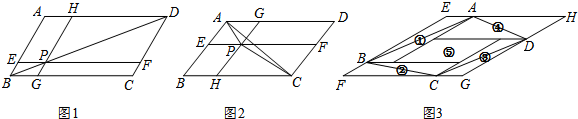
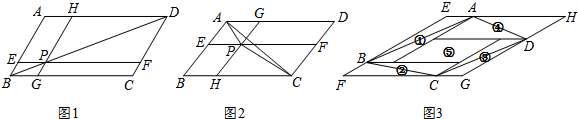
(1)人教版八年级数学下册92页第14题是这样叙述的:如图1,▱ABCD中,过对角线BD上一点P作EF∥BC,HG∥AB,图中哪两个平行四边形的面积相等?为什么?
根据习题背景,写出面积相等的一对平行四边形的名称为
▱AEPH
▱AEPH
和
▱PGCF
▱PGCF
;
(2)如图2,点P为▱ABCD内一点,过点P分别作AD、AB的平行线分别交▱ABCD的四边于点E、F、G、H.已知S
▱BHPE=3,S
▱PFDG=5,则S
△PAC=
1
1
;
(3)如图3,若①②③④⑤五个平行四边形拼成一个含30°内角的菱形EFGH(不重复、无缝隙).已知①②③④四个平行四边形面积的和为14,四边形ABCD的面积为11,则菱形EFGH的周长为
24
24
.
查看答案和解析>>
科目:czsx
来源:
题型:
现行人教版数学课本七年级(上)封面的面积大约为( )
查看答案和解析>>
科目:czsx
来源:
题型:
(1)新人教版初中数学教材中我们学习了:若关于x的一元二次方程ax
2+bx+c=0的两根为x
1,x
2,则
x1+x2=-,x1•x2=.根据这一性质,我们可以求出已知方程关于x
1,x
2的代数式的值.例如:已知x
1,x
2为方程x
2-2x-1=0的两根,则x
1+x
2=
,x
1•x
2=
.那么x
12+x
22=(x
1+x
2)
2-2x
1x
2=
.
请你完成以上的填空.
(2)阅读材料:已知m
2-m-1=0,n
2+n-1=0,且mn≠1.求
的值.
解:由n
2+n-1=0可知n≠0.
∴
1+-=0.∴
--1=0又m
2-m-1=0,且mn≠1,即
m≠.
∴m,
是方程x
2-x-1=0的两根.∴
m+=1.∴
=1.
(3)根据阅读材料所提供的方法及(1)的方法完成下题的解答.
已知2m
2-3m-1=0,n
2+3n-2=0,且mn≠1.求
m2+的值.
查看答案和解析>>
科目:czsx
来源:新教材新学案 数学 七年级下册
题型:044
在人教版教材七年级下册第10章“实数”的数学活动1中,教科书介绍了“对于任意一个直角三角形,都有两条直角边的平方和等于斜边的平方”,这就是著名的“勾股定理”.勾股定理是自然界最本质最基本的规律之一,很多文明古国对此都有所研究,古希腊科学家毕达哥拉斯在公元前550年左右发现了这个定理,而我国早在公元前1 100多年就有人在使用这个定理来解决实际问题.
在自然数中有很多数都符合这个定理的形式,例如,32+42=52,52+122=132,92+402=412,72+242=252……
如果把自然数的范围扩大为有理数(整数和分数),你还能找出符合上面形式的有理数吗?如果再把有理数范围扩大为实数(有理数和无理数)范围呢?
查看答案和解析>>
科目:czsx
来源:2010年广东省汕头市中考数学模拟试卷(二)(解析版)
题型:解答题
(1)新人教版初中数学教材中我们学习了:若关于x的一元二次方程ax
2+bx+c=0的两根为x
1,x
2,则
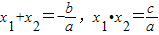
.根据这一性质,我们可以求出已知方程关于x
1,x
2的代数式的值.例如:已知x
1,x
2为方程x
2-2x-1=0的两根,则x
1+x
2=______,x
1•x
2=______.那么x
12+x
22=(x
1+x
2)
2-2x
1x
2=______.
请你完成以上的填空.
(2)阅读材料:已知m
2-m-1=0,n
2+n-1=0,且mn≠1.求
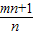
的值.
解:由n
2+n-1=0可知n≠0.
∴
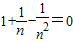
.∴
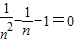
又m
2-m-1=0,且mn≠1,即
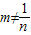
.
∴m,
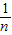
是方程x
2-x-1=0的两根.∴
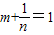
.∴
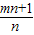
=1.
(3)根据阅读材料所提供的方法及(1)的方法完成下题的解答.
已知2m
2-3m-1=0,n
2+3n-2=0,且mn≠1.求
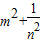
的值.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
(1)人教版八年级数学下册92页第14题是这样叙述的:如图1,▱ABCD中,过对角线BD上一点P作EF∥BC,HG∥AB,图中哪两个平行四边形的面积相等?为什么?
根据习题背景,写出面积相等的一对平行四边形的名称为______和______;
(2)如图2,点P为▱ABCD内一点,过点P分别作AD、AB的平行线分别交▱ABCD的四边于点E、F、G、H.已知S▱BHPE=3,S▱PFDG=5,则S△PAC=______;
(3)如图3,若①②③④⑤五个平行四边形拼成一个含30°内角的菱形EFGH(不重复、无缝隙).已知①②③④四个平行四边形面积的和为14,四边形ABCD的面积为11,则菱形EFGH的周长为______.
查看答案和解析>>
科目:czsx
来源:不详
题型:单选题
现行人教版数学课本七年级(上)封面的面积大约为( )
| A.480cm2 | B.200cm2 | C.48cm2 | D.20cm2 |
查看答案和解析>>
科目:czsx
来源:2011年广东省汕头市中考数学模拟试卷(解析版)
题型:解答题
(1)新人教版初中数学教材中我们学习了:若关于x的一元二次方程ax
2+bx+c=0的两根为x
1,x
2,则
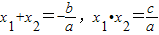
.根据这一性质,我们可以求出已知方程关于x
1,x
2的代数式的值.例如:已知x
1,x
2为方程x
2-2x-1=0的两根,则x
1+x
2=______,x
1•x
2=______.那么x
12+x
22=(x
1+x
2)
2-2x
1x
2=______.
请你完成以上的填空.
(2)阅读材料:已知m
2-m-1=0,n
2+n-1=0,且mn≠1.求
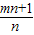
的值.
解:由n
2+n-1=0可知n≠0.
∴
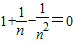
.∴
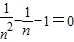
又m
2-m-1=0,且mn≠1,即
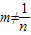
.
∴m,
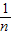
是方程x
2-x-1=0的两根.∴
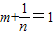
.∴
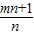
=1.
(3)根据阅读材料所提供的方法及(1)的方法完成下题的解答.
已知2m
2-3m-1=0,n
2+3n-2=0,且mn≠1.求
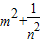
的值.
查看答案和解析>>
科目:czsx
来源:
题型:单选题
现行人教版数学课本七年级(上)封面的面积大约为
- A.
480cm2
- B.
200cm2
- C.
48cm2
- D.
20cm2
查看答案和解析>>
科目:czsx
来源:
题型:

20、某中学组织初三数学竞赛,要求每班各选出5名学生参加预选赛.如图是初三(1)班和初三(2)班学生参加数学预选赛成绩的统计图.
(1)根据统计图填写下表:
|
平均数(分) |
中位数(分) |
| 初三(1)班 |
85 |
|
| 初三(2)班 |
|
80 |
(2)如果在每班参加预选赛学生中取前3名学生参加决赛,结合两班预选赛成绩情况,你认为在决赛时哪个班级实力更强?请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:

13、花都区初三数学一模考试在2008年4月16日早上8:00开始(时钟指示如图).此时时钟的时针与分针的夹角为
120
度.
查看答案和解析>>
科目:czsx
来源:
题型:

3、(人教版)如图,用半径R=3cm,r=2cm的钢球测量口小内大的内孔的直径D.测得钢球顶点与孔口平面的距离分别为a=4cm,b=2cm,则内孔直径D的大小为( )
查看答案和解析>>
科目:czsx
来源:
题型:
为了了解某校500名初三毕业生的数学成绩,随机抽取若干名学生的数学成绩统
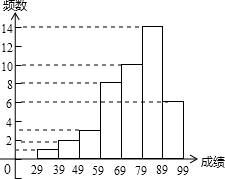
计整理后绘制如图的频数分布直方图,观察图形回答下列问题:
(1)本次随机抽查的学生人数是多少?
(2)随机抽取这些学生的平均成绩是多少?
(3)不及格的人数有多少占抽查人数的比例是多少?
(4)若80分以上的成绩为良好,试估计一下500名初三毕业生成绩良好的比例是多少?
查看答案和解析>>
科目:czsx
来源:
题型:
(人教版)计算:(-1)
2006-
(-)0+()-1
查看答案和解析>>
科目:czsx
来源:
题型:
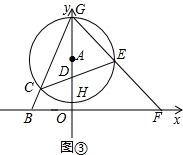
(人教版)已知平面直角坐标系中,B(-3,0),A为y轴正半轴上一动点,半径为
的⊙A交y轴于点G、H(点G在点H的上方),连接BG交⊙A于点C.
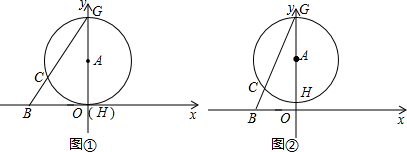
(1)如图①,当⊙A与x轴相切时,求直线BG的解析式;
(2)如图②,若CG=2BC,求OA的长;
(3)如图③,D为半径AH上一点,且AD=1,过点D作⊙A的弦CE,连接GE并延长交x轴于点F,当⊙A与x轴相离时,给出下列结论:①
的值不变;②OG•OF的值不变.其中有且只有一个结论是正确的,请你判断哪一个结论正确,证明正确的结论并求出其值.
查看答案和解析>>
科目:czsx
来源:
题型:
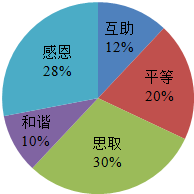
某校开展了以“人生观、价值观”为主题的班队活动.活动结束后,初三(2)班数学兴趣小组提出了5个主要观点并在本班50名学生中进行了调査(要求每位同学只选自己最认可的一项观点),并制成了如图所示的扇形统计图.
(1)该班学生选择“和谐”观点的有
人,在扇形统计图中,“和谐”观点所在扇形区域的圆心角是
.
(2)如果该校有1500名初三学生.利用样本估计选择“感恩”观点的初三学生约有
人.
(3)如果数学兴趣小组在这5个主要观点中任选两项观点在全校学生中进行调查.求恰好选到“和谐”和“感恩”观点的概率.
查看答案和解析>>
科目:czsx
来源:
题型:
某校开展了以“责任、感恩”为主题的班队活动,活动结束后,初三(2)班数学兴趣小组提出了5个主要观点并在本班学生中进行了调查(要求每位同学只选自己最认可的一项观点),并制成了如下扇形统计图,
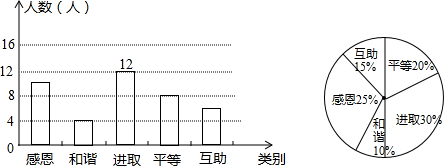
(1)该班有
40
40
人,学生选择“和谐”观点的有
4
4
人,在扇形统计图中,“和谐”观点所在扇形区域的圆心角是
36
36
度;
(2)如果该校有360名初三学生,利用样本估计选择“感恩”观点的初三学生约有
90
90
人;
(3)如果数学兴趣小组在这5个主要观点中任选两项观点在全校学生中进行调查,求恰好选到“和谐”和“感恩”观点的概率(用树状图或列表法分析解答).
查看答案和解析>>
科目:czsx
来源:
题型:

7、下图某校初三两个班100名学生参加初三数学会考所得成绩统计图,(均为整数)根据图中数据可得出该次考试优秀的(80分及80分以上)同学的人数是( )
查看答案和解析>>
科目:czsx
来源:
题型:
18、“在一次考试中,考生有2万多名,如果为了得到这些考生的数学成绩的平均水平,若将他们的成绩全部相加再除以考生的总数,那将是十分麻烦的,那么怎样才能了解这些考生的数学平均成绩呢”“通常,在考生很多的情况下,我们是从中抽取部分考生(比如500名)的成绩,用他们的平均成绩去估计所有考生的平均成绩.”
在上述文字表述中,提到了调查的两种方式是
抽样调查
和
全面调查
;反映了用样本估计总体的数学思想,其中,总体是
2万多名考生的数学平均成绩
,样本是
500名考生的数学平均成绩
,请用较简洁的语言,举一个在实际生活中,运用同种思想解决问题的例子,写在下面:
为了了解某市1万多名初三毕业生的数学平均成绩,从中抽取500名考生的数学成绩,用他们的平均成绩去估计所有考生的平均成绩.
.
查看答案和解析>>


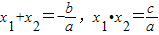 .根据这一性质,我们可以求出已知方程关于x1,x2的代数式的值.例如:已知x1,x2为方程x2-2x-1=0的两根,则x1+x2=______,x1•x2=______.那么x12+x22=(x1+x2)2-2x1x2=______.
.根据这一性质,我们可以求出已知方程关于x1,x2的代数式的值.例如:已知x1,x2为方程x2-2x-1=0的两根,则x1+x2=______,x1•x2=______.那么x12+x22=(x1+x2)2-2x1x2=______.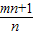 的值.
的值.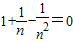 .∴
.∴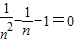
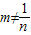 .
.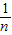 是方程x2-x-1=0的两根.∴
是方程x2-x-1=0的两根.∴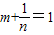 .∴
.∴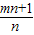 =1.
=1.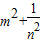 的值.
的值.
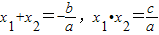 .根据这一性质,我们可以求出已知方程关于x1,x2的代数式的值.例如:已知x1,x2为方程x2-2x-1=0的两根,则x1+x2=______,x1•x2=______.那么x12+x22=(x1+x2)2-2x1x2=______.
.根据这一性质,我们可以求出已知方程关于x1,x2的代数式的值.例如:已知x1,x2为方程x2-2x-1=0的两根,则x1+x2=______,x1•x2=______.那么x12+x22=(x1+x2)2-2x1x2=______.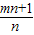 的值.
的值.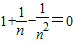 .∴
.∴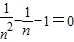
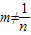 .
.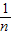 是方程x2-x-1=0的两根.∴
是方程x2-x-1=0的两根.∴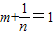 .∴
.∴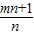 =1.
=1.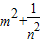 的值.
的值. 20、某中学组织初三数学竞赛,要求每班各选出5名学生参加预选赛.如图是初三(1)班和初三(2)班学生参加数学预选赛成绩的统计图.
20、某中学组织初三数学竞赛,要求每班各选出5名学生参加预选赛.如图是初三(1)班和初三(2)班学生参加数学预选赛成绩的统计图. 3、(人教版)如图,用半径R=3cm,r=2cm的钢球测量口小内大的内孔的直径D.测得钢球顶点与孔口平面的距离分别为a=4cm,b=2cm,则内孔直径D的大小为( )
3、(人教版)如图,用半径R=3cm,r=2cm的钢球测量口小内大的内孔的直径D.测得钢球顶点与孔口平面的距离分别为a=4cm,b=2cm,则内孔直径D的大小为( ) 计整理后绘制如图的频数分布直方图,观察图形回答下列问题:
计整理后绘制如图的频数分布直方图,观察图形回答下列问题:

 某校开展了以“人生观、价值观”为主题的班队活动.活动结束后,初三(2)班数学兴趣小组提出了5个主要观点并在本班50名学生中进行了调査(要求每位同学只选自己最认可的一项观点),并制成了如图所示的扇形统计图.
某校开展了以“人生观、价值观”为主题的班队活动.活动结束后,初三(2)班数学兴趣小组提出了5个主要观点并在本班50名学生中进行了调査(要求每位同学只选自己最认可的一项观点),并制成了如图所示的扇形统计图.
 7、下图某校初三两个班100名学生参加初三数学会考所得成绩统计图,(均为整数)根据图中数据可得出该次考试优秀的(80分及80分以上)同学的人数是( )
7、下图某校初三两个班100名学生参加初三数学会考所得成绩统计图,(均为整数)根据图中数据可得出该次考试优秀的(80分及80分以上)同学的人数是( )