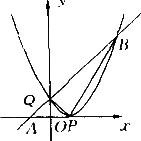科目:czsx 来源: 题型:
| 3 |
| 1 |
| 3 |
| 3 |
| 1 |
| 2 |
 不存在,请说明理由.
不存在,请说明理由. 科目:czsx 来源: 题型:
 点A在点B的左边,点O为坐标原点,
点A在点B的左边,点O为坐标原点,科目:czsx 来源:2002年浙江省台州市中考数学试卷(解析版) 题型:解答题
科目:czsx 来源:2013-2014学年北京市东城区初三第一学期期末统一测试数学试卷(解析版) 题型:解答题
在平面直角坐标系xOy中,二次函数y=-x2+(m-1)x+4m的图象与x轴负半轴交于点A,与y轴交于点B(0,4),已知点E(0,1).

(1)求m的值及点A的坐标;
(2)如图,将△AEO沿x轴向右平移得到△A′E′O′,连结A′B、BE′.
①当点E′落在该二次函数的图象上时,求AA′的长;
②设AA′=n,其中0<n<2,试用含n的式子表示A′B2+BE′2,并求出使A′B2+BE′2取得最小值时点E′的坐标;
③当A′B+BE′取得最小值时,求点E′的坐标.
科目:czsx 来源: 题型:解答题
 点A在点B的左边,点O为坐标原点,
点A在点B的左边,点O为坐标原点,科目:czsx 来源:2012年广西玉林市、防城港市中考数学试卷(解析版) 题型:填空题
 的图象与x轴围成的封闭区域内(包括边界),横、纵坐标都是整数的点有 个(提示:必要时可利用下面的备用图画出图象来分析).
的图象与x轴围成的封闭区域内(包括边界),横、纵坐标都是整数的点有 个(提示:必要时可利用下面的备用图画出图象来分析).
科目:czsx 来源:2011-2012学年江苏省九年级下学期第一次月考试数学卷 题型:解答题
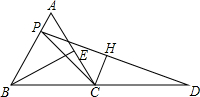
(12分)如图,二次函数y=ax2-2ax+的图象与x轴交于A、B二点,与y轴交于C点.抛物线的顶点为E(1,2),D为抛物线上一点,且CD∥x轴.
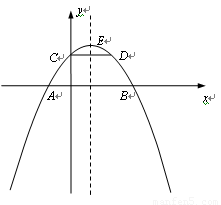
1.(1)求此二次函数的关系式;
2.(2)写出A、B、C、D四点的坐标;
3.(3)若点F在抛物线的对称轴上,点G在抛物线上,且以A、B、F、G四点为顶点的四边形为平行四边形,求点G 的坐标.
科目:czsx 来源:2013年初中毕业升学考试(四川南充卷)数学(解析版) 题型:解答题
(2013年四川南充8分)如图,二次函数y=x2+bx-3b+3的图象与x轴交于A、B两点(点A在点B的左边),交y轴于点C,且经过点(b-2,2b2-5b-1).
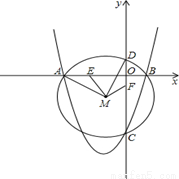
(1)求这条抛物线的解析式;
(2)⊙M过A、B、C三点,交y轴于另一点D,求点M的坐标;
(3)连接AM、DM,将∠AMD绕点M顺时针旋转,两边MA、MD与x轴、y轴分别交于点E、F,若△DMF为等腰三角形,求点E的坐标.
科目:czsx 来源:2012届江苏省洋思中学九年级下学期第一次月考试数学卷 题型:解答题
(12分)如图,二次函数y=ax2-2ax+的图象与x轴交于A、B二点,与y轴交于C点.抛物线的顶点为E(1,2),D为抛物线上一点,且CD∥x轴.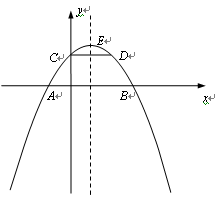
【小题1】(1)求此二次函数的关系式;
【小题2】(2)写出A、B、C、D四点的坐标;
【小题3】(3)若点F在抛物线的对称轴 上,点G在抛物线上,且以A、B、F、G四点为顶点的四边形为平行四边形,求点G 的坐标.
上,点G在抛物线上,且以A、B、F、G四点为顶点的四边形为平行四边形,求点G 的坐标.
科目:czsx 来源:2002年全国中考数学试题汇编《二次函数》(04)(解析版) 题型:解答题

科目:czsx 来源:2012年初中毕业升学考试(山东日照卷)数学(带解析) 题型:解答题
如图,二次函数y=x2+bx+c的图象与x轴交于A、B两点,且A点坐标为
(-3,0),经过B点的直线交抛物线于点D(-2,-3).
(1)求抛物线的解析式和直线BD解析式;
(2)过x轴上点E(a,0)(E点在B点的右侧)作直线EF∥BD,交抛物线于点F,是否存在实数a使四边形BDFE是平行四边形?如果存在,求出满足条件的a;如果不存在,请说明理由.
科目:czsx 来源:2012年初中毕业升学考试(山东日照卷)数学(解析版) 题型:解答题
如图,二次函数y=x2+bx+c的图象与x轴交于A、B两点,且A点坐标为
(-3,0),经过B点的直线交抛物线于点D(-2,-3).
(1)求抛物线的解析式和直线BD解析式;
(2)过x轴上点E(a,0)(E点在B点的右侧)作直线EF∥BD,交抛物线于点F,是否存在实数a使四边形BDFE是平行四边形?如果存在,求出满足条件的a;如果不存在,请说明理由.

科目:czsx 来源:2011-2012学年湖北省广水市九年级下学期月考数学试卷(解析版) 题型:选择题
如图,二次函数y=ax2+bx+c的图象与y轴正半轴相交,其顶点坐标为 ,下列结论:
,下列结论:
①ac<0;②a+b=0;③4ac-b2=4a;④a+b+c<0.其中正确的个数是( )

A. 1 B. 2 C. 3 D. 4
科目:czsx 来源: 题型:
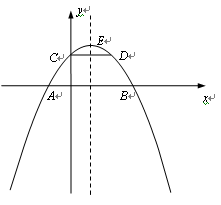
 上,点G在抛物线上,且以A、B、F、G四点为顶点的四边形为平行四边形,求点G 的坐标.
上,点G在抛物线上,且以A、B、F、G四点为顶点的四边形为平行四边形,求点G 的坐标. 科目:czsx 来源: 题型:
(2013四川南充,21,8分)如图,二次函数y=x2+bx-3b+3的图象与x轴交于A、B两点(点A在点B的左边),交y轴于点C,且经过点(b-2,2b2-5b-1).
(1)求这条抛物线的解析式;
(2)⊙M过A、B、C三点,交y轴于另一点D,求点M的坐标;
(3)连接AM、DM,将∠AMD绕点M顺时针旋转,两边MA、MD与x轴、y轴分别交于点E、F,若△DMF为等腰三角形,求点E的坐标.

科目:czsx 来源:新教材完全解读 九年级数学 下册(配北师大版新课标) 北师大版新课标 题型:044
如图所示,二次函数y=x2+bx-c的图象与x轴只有一个公共点P,与y轴的交点为Q,过点Q的直线y=2x+m与x轴交于点A,与这个二次函数的图象交于另一点B,若S△BPQ=3S△APQ,求这个二次函数的解析式.