
科目:gzsx 来源: 题型:
已知图4(1)中的图象对应的函数为y=f(x),则图4(2)中的图象对应的函数在下列给出的四式中,只可能是( )
 |
A.y=f(|x|) B.y=|f(x)| C.y=f(-|x|) D.y=-f(|x|)
科目:gzsx 来源: 题型:
已知图4(1)中的图象对应的函数为y=f(x),则图4(2)中的图象对应的函数在下列给出的四式中,只可能是( )
 |
A.y=f(|x|) B.y=|f(x)| C.y=f(-|x|) D.y=-f(|x|)
科目:gzsx 来源:2011-2012学年江西省南昌市高三第二次模拟测试理科数学试卷(解析版) 题型:解答题
(本小题满分14分)
(1)已知等差数列{an}的前n项和为Sn,若m+n=s+t(m,n,s,t∈N*,且m≠n,s≠t),证明;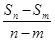 =
= 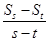 ;
;
(2)注意到(1)中Sn与n的函数关系,我们得到命题:设抛物线x2=2py(p>0)的图像上有不同的四点A,B,C,D,若xA,xB,xC,xD分别是这四点的横坐标,且xA+xB=xC+xD,则AB∥CD,判定这个命题的真假,并证明你的结论
(3)我们知道椭圆和抛物线都是圆锥曲线,根据(2)中的结论,对椭圆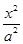 +
+ =1(a>b>0)提出一个有深度的结论,并证明之.
=1(a>b>0)提出一个有深度的结论,并证明之.
科目:gzsx 来源: 题型:
| 1 | 4x2 |
科目:gzsx 来源:2011-2012学年上海市长宁区高三教学质量测试理科数学 题型:解答题
(本小题满分18分) 本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.
(文)已知数列 中,
中,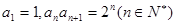
(1)求证数列 不是等比数列,并求该数列的通项公式;
不是等比数列,并求该数列的通项公式;
(2)求数列 的前
的前 项和
项和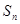 ;
;
(3)设数列 的前
的前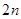 项和为
项和为 ,若
,若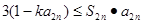 对任意
对任意 恒成立,求
恒成立,求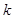 的最小值.
的最小值.
科目:gzsx 来源:2011-2012学年甘肃省高三上学期期中考试理科数学试卷 题型:解答题
(本题12分)已知数列{an}中,a1=0,a2
=4,且an+2-3an+1+2an= 2n+1(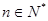 ),
),
数列{bn}满足bn=an+1-2an.
(Ⅰ)求证:数列{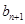 -
- }是等比数列;
}是等比数列;
(Ⅱ)求数列{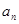 }的通项公式;
}的通项公式;
(Ⅲ)求 .
.
科目:gzsx 来源:2012届甘肃省兰州一中高三上学期期中考试理科数学试卷 题型:解答题
(本题12分)已知数列{an}中,a1=0,a2 =4,且an+2-3an+1+2an= 2n+1(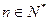 ),
),
数列{bn}满足bn=an+1-2an.
(Ⅰ)求证:数列{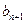 -
- }是等比数列;
}是等比数列;
(Ⅱ)求数列{ }的通项公式;
}的通项公式;
(Ⅲ)求 .
.
科目:gzsx 来源:湖南省高考真题 题型:解答题
 。
。 科目:gzsx 来源: 题型:
(1)求证:数列{an}是等比数列;
(2)若a=![]() ,数列{bn}满足bn=
,数列{bn}满足bn=![]() log2(a1a2…an)(n=1,2,…,2k),求数列{bn}的通项公式;
log2(a1a2…an)(n=1,2,…,2k),求数列{bn}的通项公式;
(3)若(2)中的数列{bn}满足不等式.
|b1-![]() |+|b2-
|+|b2-![]() |+…+|b2k-1-
|+…+|b2k-1-![]() |+|b2k-
|+|b2k-![]() |≤4,求k的值.
|≤4,求k的值.
科目:gzsx 来源:专项题 题型:解答题

 。
。科目:gzsx 来源: 题型:
已知有穷数列![]() 共有2
共有2![]() 项(整数
项(整数![]() ≥2),首项
≥2),首项![]() =2.设该数列的前
=2.设该数列的前![]() 项和为
项和为![]() ,且
,且![]() =
=![]() +2(
+2(![]() =1,2,┅,2
=1,2,┅,2![]() -1),其中常数
-1),其中常数![]() >1.
>1.
(1)求证:数列![]() 是等比数列;
是等比数列;
(2)若![]() =2
=2![]() ,数列
,数列![]() 满足
满足![]() =
=![]() (
(![]() =1,2,┅,2
=1,2,┅,2![]() ),求数列
),求数列![]() 的通项公式;
的通项公式;
(3)若(2)中的数列![]() 满足不等式|
满足不等式|![]() -
-![]() |+|
|+|![]() -
-![]() |+┅+|
|+┅+|![]() -
-![]() |+|
|+|![]() -
-![]() |≤4,求
|≤4,求![]() 的值.
的值.
科目:gzsx 来源:不详 题型:解答题
| 1 |
| 4x2 |
科目:gzsx 来源: 题型:
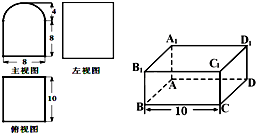 (1)已知某个几何体的三视图如图(主视图的弧线是半圆),根据图中的数据,求这个组合体的体积;
(1)已知某个几何体的三视图如图(主视图的弧线是半圆),根据图中的数据,求这个组合体的体积;科目:gzsx 来源: 题型:
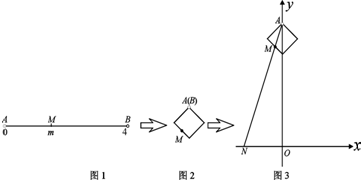 下图展示了一个由区间(0,4)到实数集R的映射过程:区间(0,4)中的实数m对应数轴上的点M(如图1),将线段AB围成一个正方形,使两端点A,B恰好重合(如图2),再将这个正方形放在平面直角坐标系中,使其中两个顶点在y轴上,点A的坐标为(0,4)(如图3),若图3中直线AM与x轴交于点N(n,0),则m的象就是n,记作f(m)=n.
下图展示了一个由区间(0,4)到实数集R的映射过程:区间(0,4)中的实数m对应数轴上的点M(如图1),将线段AB围成一个正方形,使两端点A,B恰好重合(如图2),再将这个正方形放在平面直角坐标系中,使其中两个顶点在y轴上,点A的坐标为(0,4)(如图3),若图3中直线AM与x轴交于点N(n,0),则m的象就是n,记作f(m)=n.科目:gzsx 来源: 题型:
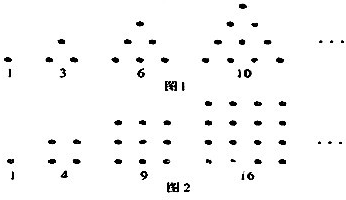
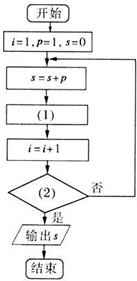 给出50个数;1,2,6,24,120,…,其规律是:第1个数是1,第2个数是第1个数乘以2所得的积,第3个数是第2个数乘以3所得的积,第4个数是第3个数乘以4所得的积…,依此类推,要计算这50个数的和,现已给出了该问题算法的程序框图(如图所示),
给出50个数;1,2,6,24,120,…,其规律是:第1个数是1,第2个数是第1个数乘以2所得的积,第3个数是第2个数乘以3所得的积,第4个数是第3个数乘以4所得的积…,依此类推,要计算这50个数的和,现已给出了该问题算法的程序框图(如图所示),科目:gzsx 来源: 题型:
| A、289 | B、1024 | C、1225 | D、1378 |
科目:gzsx 来源: 题型:
| an-an-1 | 2 |
科目:gzsx 来源: 题型:
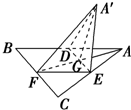 如图,边长为a的正△ABC的中线AF与中位线DE相交于G,已知△A′ED是△AED绕DE旋转过程中的一个图形,现给出下列命题,其中正确的命题有
如图,边长为a的正△ABC的中线AF与中位线DE相交于G,已知△A′ED是△AED绕DE旋转过程中的一个图形,现给出下列命题,其中正确的命题有科目:gzsx 来源: 题型:
| n |
 |
| i=1 |
| 1 |
| 1+ai |
| 1 |
| 2 |
| bn+1 |
| bn |
| bk+1 |
| bk |