精英家教网 >
试题搜索列表 >如图,∠BAC=∠BDA=∠CEA=90°,AB=AC,若BD=3,CE=2,则DE
如图,∠BAC=∠BDA=∠CEA=90°,AB=AC,若BD=3,CE=2,则DE答案解析
科目:czsx
来源:
题型:
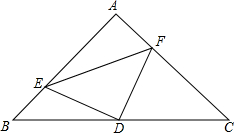
已知:如图△ABC中,∠A=90°,AB=AC,D是斜边BC的中点,E,F分别在线段AB,AC上,且∠EDF=90°
(1)求证:△DEF为等腰直角三角形;
(2)求证:S
四边形AEDF=S
△BDE+S
△CDF;
(3)如果点E运动到AB的延长线上,F在射线CA上且保持∠EDF=90°,△DEF还仍然是等腰直角三角形吗?请画图说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
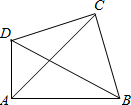
已知:如图Rt△ABD和Rt△BCD如图放置,∠BAD=∠BCD=90°,连接AC,若AC平分∠DAB,则线段AB、AD、AC有怎样的数量关系?写出你的猜想,并证明.
查看答案和解析>>
科目:czsx
来源:
题型:
黄金分割比是生活中比较多见的一种长度比值,它能给人许多美感和科学性,我们初中阶段学过的许多几何图形也有着类似的边长比例关系.例如我们熟悉的顶角是36°的等腰三角形,其底与腰之比就为黄金分割比
,底角平分线与腰的交点为黄金分割点.
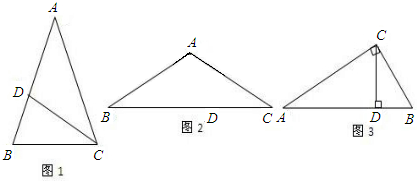
(1)如图1,在△ABC中,∠A=36°,AB=AC,∠ACB的角平分线CD交腰AB于点D,请你证明点D是腰AB的黄金分割点;
(2)如图2,在△ABC中,AB=AC,若
=,则请你求出∠A的度数;
(3)如图3,如果在Rt△ABC中,∠ACB=90°,CD为AB上的高,∠A、∠B、∠ACB的对边分别为a,b,c.若点D是AB的黄金分割点,那么该直角三角形的三边a,b,c之间是什么数量关系?并证明你的结论.
查看答案和解析>>
科目:czsx
来源:
题型:
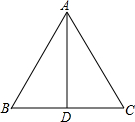
如图,△ABC是一个屋架,AB=AC.若D为BC的中点,下列结论中:①△ABD≌△ACD;②AD⊥BC;③AD平分∠BAC;④∠B=∠C=60°.其中不正确的是
④
④
.(填序号)
查看答案和解析>>
科目:czsx
来源:2010年浙江省湖州市八年级上学期期中考试数学卷
题型:解答题
已知:如图Rt△ABD和Rt△BCD如图放置,∠BAD=∠BCD =90°,连结AC,若AC平分∠DAB,则线段AB、AD、AC有怎样的数量关系?写出你的猜想,并证明.

查看答案和解析>>
科目:czsx
来源:
题型:
已知:如图Rt△ABD和Rt△BCD如图放置,∠B
AD=∠B
CD =90°,连结AC,若AC平分∠DAB,则线段AB、AD、AC有怎样的数量关系?写出你的猜想,并证明.

查看答案和解析>>
科目:czsx
来源:2012年浙江省湖州市南浔区中考数学一模试卷(解析版)
题型:解答题
黄金分割比是生活中比较多见的一种长度比值,它能给人许多美感和科学性,我们初中阶段学过的许多几何图形也有着类似的边长比例关系.例如我们熟悉的顶角是36°的等腰三角形,其底与腰之比就为黄金分割比
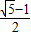
,底角平分线与腰的交点为黄金分割点.
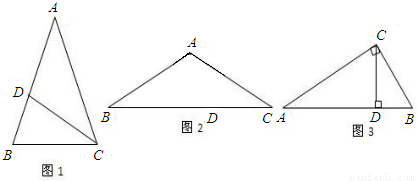
(1)如图1,在△ABC中,∠A=36°,AB=AC,∠ACB的角平分线CD交腰AB于点D,请你证明点D是腰AB的黄金分割点;
(2)如图2,在△ABC中,AB=AC,若

,则请你求出∠A的度数;
(3)如图3,如果在Rt△ABC中,∠ACB=90°,CD为AB上的高,∠A、∠B、∠ACB的对边分别为a,b,c.若点D是AB的黄金分割点,那么该直角三角形的三边a,b,c之间是什么数量关系?并证明你的结论.
查看答案和解析>>
科目:czsx
来源:2010年数学参赛试卷2010.3吴(解析版)
题型:解答题
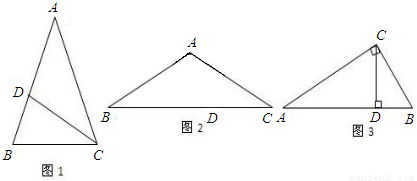
(2012•南浔区一模)黄金分割比是生活中比较多见的一种长度比值,它能给人许多美感和科学性,我们初中阶段学过的许多几何图形也有着类似的边长比例关系.例如我们熟悉的顶角是36°的等腰三角形,其底与腰之比就为黄金分割比
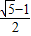
,底角平分线与腰的交点为黄金分割点.
(1)如图1,在△ABC中,∠A=36°,AB=AC,∠ACB的角平分线CD交腰AB于点D,请你证明点D是腰AB的黄金分割点;
(2)如图2,在△ABC中,AB=AC,若
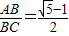
,则请你求出∠A的度数;
(3)如图3,如果在Rt△ABC中,∠ACB=90°,CD为AB上的高,∠A、∠B、∠ACB的对边分别为a,b,c.若点D是AB的黄金分割点,那么该直角三角形的三边a,b,c之间是什么数量关系?并证明你的结论.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
黄金分割比是生活中比较多见的一种长度比值,它能给人许多美感和科学性,我们初中阶段学过的许多几何图形也有着类似的边长比例关系.例如我们熟悉的顶角是36°的等腰三角形,其底与腰之比就为黄金分割比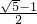 ,底角平分线与腰的交点为黄金分割点.
,底角平分线与腰的交点为黄金分割点.
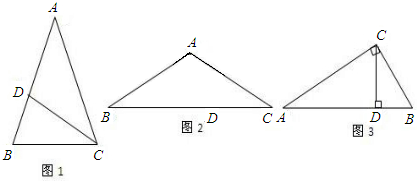
(1)如图1,在△ABC中,∠A=36°,AB=AC,∠ACB的角平分线CD交腰AB于点D,请你证明点D是腰AB的黄金分割点;
(2)如图2,在△ABC中,AB=AC,若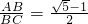 ,则请你求出∠A的度数;
,则请你求出∠A的度数;
(3)如图3,如果在Rt△ABC中,∠ACB=90°,CD为AB上的高,∠A、∠B、∠ACB的对边分别为a,b,c.若点D是AB的黄金分割点,那么该直角三角形的三边a,b,c之间是什么数量关系?并证明你的结论.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
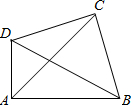 已知:如图Rt△ABD和Rt△BCD如图放置,∠BAD=∠BCD=90°,连接AC,若AC平分∠DAB,则线段AB、AD、AC有怎样的数量关系?写出你的猜想,并证明.
已知:如图Rt△ABD和Rt△BCD如图放置,∠BAD=∠BCD=90°,连接AC,若AC平分∠DAB,则线段AB、AD、AC有怎样的数量关系?写出你的猜想,并证明.
查看答案和解析>>
科目:czsx
来源:不详
题型:填空题
如图,△ABC是一个屋架,AB=AC.若D为BC的中点,下列结论中:①△ABD≌△ACD;②AD⊥BC;③AD平分∠BAC;④∠B=∠C=60°.其中不正确的是______.(填序号)
查看答案和解析>>
科目:czsx
来源:
题型:解答题
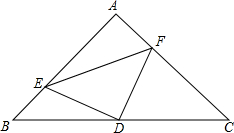 已知:如图△ABC中,∠A=90°,AB=AC,D是斜边BC的中点,E,F分别在线段AB,AC上,且∠EDF=90°
已知:如图△ABC中,∠A=90°,AB=AC,D是斜边BC的中点,E,F分别在线段AB,AC上,且∠EDF=90°
(1)求证:△DEF为等腰直角三角形;
(2)求证:S四边形AEDF=S△BDE+S△CDF;
(3)如果点E运动到AB的延长线上,F在射线CA上且保持∠EDF=90°,△DEF还仍然是等腰直角三角形吗?请画图说明理由.
查看答案和解析>>
科目:czsx
来源:2010年浙江省湖州市菱湖一中八年级上学期期中考试数学卷
题型:解答题
已知:如图Rt△ABD和Rt△BCD如图放置,∠BAD=∠BCD =90°,连结AC,若AC平分∠DAB,则线段AB、AD、AC有怎样的数量关系?写出你的猜想,并证明.
查看答案和解析>>
科目:czsx
来源:
题型:
已知:如图Rt△ABD和Rt△BCD如图放置,∠BAD=∠BCD =90°,连结AC,若AC平分∠DAB,则线段AB、AD、AC有怎样的数量关系?写出你的猜想,并证明.

查看答案和解析>>
科目:czsx
来源:
题型:填空题
 如图,△ABC是一个屋架,AB=AC.若D为BC的中点,下列结论中:①△ABD≌△ACD;②AD⊥BC;③AD平分∠BAC;④∠B=∠C=60°.其中不正确的是________.(填序号)
如图,△ABC是一个屋架,AB=AC.若D为BC的中点,下列结论中:①△ABD≌△ACD;②AD⊥BC;③AD平分∠BAC;④∠B=∠C=60°.其中不正确的是________.(填序号)
查看答案和解析>>
科目:czsx
来源:
题型:

26、如图,△ABC内一点P,AB=AC,若∠APB=∠APC,求证:∠PBC=∠PCB.
查看答案和解析>>
科目:czsx
来源:2010-2011学年北京市四中九年级(上)月考数学试卷(10月份)(解析版)
题型:解答题
如图,△ABC内一点P,AB=AC,若∠APB=∠APC,求证:∠PBC=∠PCB.

查看答案和解析>>
科目:czsx
来源:
题型:解答题
 如图,△ABC内一点P,AB=AC,若∠APB=∠APC,求证:∠PBC=∠PCB.
如图,△ABC内一点P,AB=AC,若∠APB=∠APC,求证:∠PBC=∠PCB.
查看答案和解析>>
科目:czsx
来源:同步题
题型:解答题
如图,在等腰△ABC 中,AB=AC,若AB=2BC,求∠B的正弦值和正切值。
查看答案和解析>>
科目:czsx
来源:
题型:
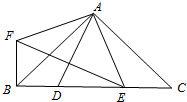
如图,在Rt△ABC中,AB=AC,∠BAC=90°,D、E为BC上两点,∠DAE=45°,F为△ABC外一点,且FB⊥BC,FA⊥AE,则下列结论:①CE=BF;②BD
2+CE
2=DE
2;③
S△ADE=AD•EF;④CE
2+BE
2=2AE
2,其中正确的是( )
查看答案和解析>>

 已知:如图△ABC中,∠A=90°,AB=AC,D是斜边BC的中点,E,F分别在线段AB,AC上,且∠EDF=90°
已知:如图△ABC中,∠A=90°,AB=AC,D是斜边BC的中点,E,F分别在线段AB,AC上,且∠EDF=90° 已知:如图Rt△ABD和Rt△BCD如图放置,∠BAD=∠BCD=90°,连接AC,若AC平分∠DAB,则线段AB、AD、AC有怎样的数量关系?写出你的猜想,并证明.
已知:如图Rt△ABD和Rt△BCD如图放置,∠BAD=∠BCD=90°,连接AC,若AC平分∠DAB,则线段AB、AD、AC有怎样的数量关系?写出你的猜想,并证明.
 如图,△ABC是一个屋架,AB=AC.若D为BC的中点,下列结论中:①△ABD≌△ACD;②AD⊥BC;③AD平分∠BAC;④∠B=∠C=60°.其中不正确的是
如图,△ABC是一个屋架,AB=AC.若D为BC的中点,下列结论中:①△ABD≌△ACD;②AD⊥BC;③AD平分∠BAC;④∠B=∠C=60°.其中不正确的是

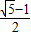 ,底角平分线与腰的交点为黄金分割点.
,底角平分线与腰的交点为黄金分割点. ,则请你求出∠A的度数;
,则请你求出∠A的度数;
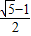 ,底角平分线与腰的交点为黄金分割点.
,底角平分线与腰的交点为黄金分割点.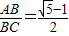 ,则请你求出∠A的度数;
,则请你求出∠A的度数;
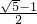 ,底角平分线与腰的交点为黄金分割点.
,底角平分线与腰的交点为黄金分割点.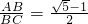 ,则请你求出∠A的度数;
,则请你求出∠A的度数;
 已知:如图Rt△ABD和Rt△BCD如图放置,∠BAD=∠BCD=90°,连接AC,若AC平分∠DAB,则线段AB、AD、AC有怎样的数量关系?写出你的猜想,并证明.
已知:如图Rt△ABD和Rt△BCD如图放置,∠BAD=∠BCD=90°,连接AC,若AC平分∠DAB,则线段AB、AD、AC有怎样的数量关系?写出你的猜想,并证明.
 已知:如图△ABC中,∠A=90°,AB=AC,D是斜边BC的中点,E,F分别在线段AB,AC上,且∠EDF=90°
已知:如图△ABC中,∠A=90°,AB=AC,D是斜边BC的中点,E,F分别在线段AB,AC上,且∠EDF=90°

 如图,△ABC是一个屋架,AB=AC.若D为BC的中点,下列结论中:①△ABD≌△ACD;②AD⊥BC;③AD平分∠BAC;④∠B=∠C=60°.其中不正确的是________.(填序号)
如图,△ABC是一个屋架,AB=AC.若D为BC的中点,下列结论中:①△ABD≌△ACD;②AD⊥BC;③AD平分∠BAC;④∠B=∠C=60°.其中不正确的是________.(填序号)
 如图,在Rt△ABC中,AB=AC,∠BAC=90°,D、E为BC上两点,∠DAE=45°,F为△ABC外一点,且FB⊥BC,FA⊥AE,则下列结论:①CE=BF;②BD2+CE2=DE2;③S△ADE=
如图,在Rt△ABC中,AB=AC,∠BAC=90°,D、E为BC上两点,∠DAE=45°,F为△ABC外一点,且FB⊥BC,FA⊥AE,则下列结论:①CE=BF;②BD2+CE2=DE2;③S△ADE=