如图,角a=角,角1=角2,ac,bd交于点o.问ab=cd答案解析
科目:czsx
来源:
题型:

25、已知,如图,在▱ABCD中,AE=CF,EF与BD交于点H,由图中可以得到许多结论,例如:AB=DC;∠A=∠C;△ADB≌△CBD;S
梯形ADFE=S
梯形BCFE;….
等等,你一定还能从图中得出许多有趣的结论,请你写出一个你认为有价值的正确结论,并证明之.
查看答案和解析>>
科目:czsx
来源:
题型:

如图,已知CP为⊙O的直径,AC切⊙O于点C,AB切⊙O于点D,并与CP的延长线相交于点B,连接PD,CD,又BD=2BP,∠BDP=∠DCP.
求证:(1)PC=3PB;(2)AC=PC.
查看答案和解析>>
科目:czsx
来源:
题型:

如图,已知AC,BD交于点D,AB∥CD,OA=OC,求证:AB=CD.
查看答案和解析>>
科目:czsx
来源:2010-2011学年浙江省衢州市菁才中学九年级(上)第三次月考数学试卷(解析版)
题型:解答题
如图,已知CP为⊙O的直径,AC切⊙O于点C,AB切⊙O于点D,并与CP的延长线相交于点B,连接PD,CD,又BD=2BP,∠BDP=∠DCP.
求证:(1)PC=3PB;(2)AC=PC.

查看答案和解析>>
科目:czsx
来源:2002年全国中考数学试题汇编《四边形》(05)(解析版)
题型:解答题
(2002•广元)已知,如图,在▱ABCD中,AE=CF,EF与BD交于点H,由图中可以得到许多结论,例如:AB=DC;∠A=∠C;△ADB≌△CBD;S
梯形ADFE=S
梯形BCFE;….等等,你一定还能从图中得出许多有趣的结论,请你写出一个你认为有价值的正确结论,并证明之.

查看答案和解析>>
科目:czsx
来源:
题型:解答题
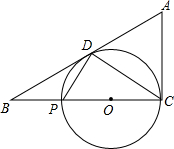 如图,已知CP为⊙O的直径,AC切⊙O于点C,AB切⊙O于点D,并与CP的延长线相交于点B,连接PD,CD,又BD=2BP,∠BDP=∠DCP.
如图,已知CP为⊙O的直径,AC切⊙O于点C,AB切⊙O于点D,并与CP的延长线相交于点B,连接PD,CD,又BD=2BP,∠BDP=∠DCP.
求证:(1)PC=3PB;(2)AC=PC.
查看答案和解析>>
科目:czsx
来源:2002年全国中考数学试题汇编《三角形》(08)(解析版)
题型:解答题
(2002•广元)已知,如图,在▱ABCD中,AE=CF,EF与BD交于点H,由图中可以得到许多结论,例如:AB=DC;∠A=∠C;△ADB≌△CBD;S
梯形ADFE=S
梯形BCFE;….等等,你一定还能从图中得出许多有趣的结论,请你写出一个你认为有价值的正确结论,并证明之.

查看答案和解析>>
科目:czsx
来源:2002年四川省广元市中考数学试卷(解析版)
题型:解答题
(2002•广元)已知,如图,在▱ABCD中,AE=CF,EF与BD交于点H,由图中可以得到许多结论,例如:AB=DC;∠A=∠C;△ADB≌△CBD;S
梯形ADFE=S
梯形BCFE;….等等,你一定还能从图中得出许多有趣的结论,请你写出一个你认为有价值的正确结论,并证明之.

查看答案和解析>>
科目:czsx
来源:课堂三级讲练数学九年级(上)
题型:022
如图,在△AOB和△COD中,AC与BD交于点O,AB∥CD,OA=OC,则△AOB≌________,理由是________.

查看答案和解析>>
科目:czsx
来源:
题型:013
如图所示,在等腰梯形ABCD中,AD∥BC,AC,BD相交于点O, 则图中全等三角形共有( )
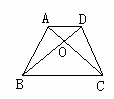
A
.
1对
B.
2对
C.
3对
D.
4对
查看答案和解析>>
科目:czsx
来源:
题型:
如图,已知CP为⊙O的直径,AC切⊙O于点C,AB切⊙O于点D,并与CP的延长线相交于点B,又BD=2 BP.求证:(1)PC=3 PB;(2)AC=PC.
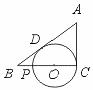
查看答案和解析>>
科目:czsx
来源:
题型:解答题
 已知,如图,在▱ABCD中,AE=CF,EF与BD交于点H,由图中可以得到许多结论,例如:AB=DC;∠A=∠C;△ADB≌△CBD;S梯形ADFE=S梯形BCFE;….等等,你一定还能从图中得出许多有趣的结论,请你写出一个你认为有价值的正确结论,并证明之.
已知,如图,在▱ABCD中,AE=CF,EF与BD交于点H,由图中可以得到许多结论,例如:AB=DC;∠A=∠C;△ADB≌△CBD;S梯形ADFE=S梯形BCFE;….等等,你一定还能从图中得出许多有趣的结论,请你写出一个你认为有价值的正确结论,并证明之.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
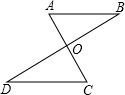 如图,已知AC,BD交于点D,AB∥CD,OA=OC,求证:AB=CD.
如图,已知AC,BD交于点D,AB∥CD,OA=OC,求证:AB=CD.
查看答案和解析>>
科目:czsx
来源:
题型:
如图,AC与BD交于点E,AB∥CD∥EF,AB=10,CD=15,则EF的长为_______.

查看答案和解析>>
科目:czsx
来源:湖北省同步题
题型:证明题
已知:如图,AC和BD交于点O,AB//CD ,OA=OB .求证:OC=OD
查看答案和解析>>
科目:czsx
来源:
题型:
(2013•威海)操作发现
将一副直角三角板如图①摆放,能够发现等腰直角三角板ABC的斜边与含30°角的直角三角板DEF的长直角边DE重合.
问题解决
将图①中的等腰直角三角板ABC绕点B顺时针旋转30°,点C落在BF上,AC与BD交于点O,连接CD,如图②.
(1)求证:△CDO是等腰三角形;
(2)若DF=8,求AD的长.

查看答案和解析>>
科目:czsx
来源:
题型:

4、如图,在△ABC中,∠A,∠B的平分线交于点O,连接CO并延长交AB边于点D,则CD是△ABC的( )
查看答案和解析>>
科目:czsx
来源:
题型:
某校七年级数学兴趣小组对“三角形内角或外角平分线的夹角与第三个内角的数量关系”进行了探究.

(1)如图1,△ABC两内角∠ABC与∠ACB的平分线交于点E.则∠BEC=90°+
∠A.
(阅读下面证明过程,并填空.)
证明:∵BE、CE分别平分∠ABC和∠ACB,
∴∠EBC=
∠ABC,∠ECB=
∠ACB(角平分线的定义)
∴∠BEC=180°-(∠EBC+∠ECB)(
三角形内角和定理
三角形内角和定理
)
=180°-(
∠ABC+∠ACB)=180°-
(∠ABC+∠ACB)
=180°-
(180°-∠A)
=
=90°+
∠A(2)如图2,△ABC的内角∠ABC的平分线与△ABC的外角∠ACM的平分线交于点E.
请你写出∠BEC与∠A的数量关系,并证明.
答:∠BEC与∠A的数量关系式:
.
证明:
如下
如下
.
(3)如图3,△ABC的两外角∠CBD与∠BCF的平分线交于点E,请你直接写出∠BEC与∠A的数量关系,不需证明.
查看答案和解析>>
科目:czsx
来源:
题型:
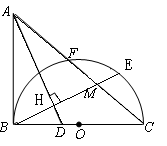
如图,已知
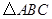
,以
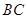
为直径,
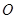
为圆心的半圆交
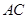
于点
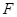
,点
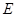
为弧CF的中点,连接
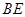
交
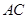
于点
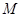
,
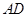
为△ABC的角平分线,且
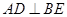
,垂足为点
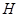
.
【小题1】求证:

是半圆
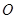
的切线;
【小题2】若
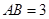
,
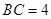
,求
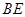
的长.
查看答案和解析>>

 25、已知,如图,在▱ABCD中,AE=CF,EF与BD交于点H,由图中可以得到许多结论,例如:AB=DC;∠A=∠C;△ADB≌△CBD;S梯形ADFE=S梯形BCFE;….
25、已知,如图,在▱ABCD中,AE=CF,EF与BD交于点H,由图中可以得到许多结论,例如:AB=DC;∠A=∠C;△ADB≌△CBD;S梯形ADFE=S梯形BCFE;…. 如图,已知CP为⊙O的直径,AC切⊙O于点C,AB切⊙O于点D,并与CP的延长线相交于点B,连接PD,CD,又BD=2BP,∠BDP=∠DCP.
如图,已知CP为⊙O的直径,AC切⊙O于点C,AB切⊙O于点D,并与CP的延长线相交于点B,连接PD,CD,又BD=2BP,∠BDP=∠DCP.

 如图,已知CP为⊙O的直径,AC切⊙O于点C,AB切⊙O于点D,并与CP的延长线相交于点B,连接PD,CD,又BD=2BP,∠BDP=∠DCP.
如图,已知CP为⊙O的直径,AC切⊙O于点C,AB切⊙O于点D,并与CP的延长线相交于点B,连接PD,CD,又BD=2BP,∠BDP=∠DCP.


 已知,如图,在▱ABCD中,AE=CF,EF与BD交于点H,由图中可以得到许多结论,例如:AB=DC;∠A=∠C;△ADB≌△CBD;S梯形ADFE=S梯形BCFE;….等等,你一定还能从图中得出许多有趣的结论,请你写出一个你认为有价值的正确结论,并证明之.
已知,如图,在▱ABCD中,AE=CF,EF与BD交于点H,由图中可以得到许多结论,例如:AB=DC;∠A=∠C;△ADB≌△CBD;S梯形ADFE=S梯形BCFE;….等等,你一定还能从图中得出许多有趣的结论,请你写出一个你认为有价值的正确结论,并证明之.

![]() ,以
,以![]() 为直径,
为直径,![]() 为圆心的半圆交
为圆心的半圆交![]() 于点
于点![]() ,点
,点![]() 为弧CF的中点,连接
为弧CF的中点,连接![]() 交
交![]() 于点
于点![]() ,
,![]() 为△ABC的角平分线,且
为△ABC的角平分线,且![]() ,垂足为点
,垂足为点![]() .
.![]() 是半圆
是半圆![]() 的切线;
的切线;![]() ,
,![]() ,求
,求![]() 的长.
的长.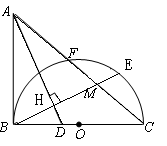
 ,以
,以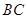 为直径,
为直径,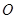 为圆心的半圆交
为圆心的半圆交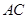 于点
于点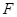 ,点
,点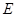 为弧CF的中点,连接
为弧CF的中点,连接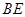 交
交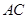 于点
于点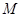 ,
,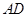 为△ABC的角平分线,且
为△ABC的角平分线,且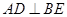 ,垂足为点
,垂足为点 .
. 是半圆
是半圆 的切线;
的切线;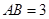 ,
,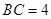 ,求
,求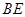 的长.
的长.