
科目:czsx 来源:走进数学世界七年级(上) 题型:044
先阅读下列短文,再解决后面的问题.
3123是一个很大的数,怎样求出它的末位数字呢?
我们依次计算一下31=3,32=9,33=27,34=81,35=243,36=729,37=2187,38=6561,……观察其末位数字的变化,寻找其中的规律,从而用归纳的方法得出结论:它们的末位数字不断循环出现3、9、7、1,周期为4.于是将指数123表示成30×4+3,得出3123和33的末位数字是相同的结论,即3123的末位数字为7.
(1)运用上面得出的规律,分别说出23123,123123,19931994,19932001的末尾数字是几?
(2)当m是怎样的多位数时,mn(n为正整数)的末位数字是不变的?
(3)运用上面的方法求出19941995,19981999,19972001的末位数字.
科目:czsx 来源:101网校同步练习 初一数学 华东师大(新课标2001-3年初审) 华东师大(新课标2001-3年初审) 题型:044
如图所示,用同样规格的黑白两色的正方形瓷砖铺设长方形地面,先请你观察下列图形,再解答后面的问题:

(1)在第n个图中,每一横行共有________块瓷砖,每一竖列共有________块瓷砖(用含有n的代数式表示).
(2)设铺设地面所用瓷砖的总数为y,请写出y与n的关系式.
(3)在第10个图中,需要白色________块,黑色________块.
科目:czsx 来源: 题型:阅读理解
| ||
| n |
科目:czsx 来源: 题型:阅读理解
| 1 |
| 1×3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3×5 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 5×7 |
| 1 |
| 2 |
| 1 |
| 5 |
| 1 |
| 7 |
| 1 |
| 17×19 |
| 1 |
| 2 |
| 1 |
| 17 |
| 1 |
| 19 |
| 1 |
| 1×3 |
| 1 |
| 3×5 |
| 1 |
| 5×7 |
| 1 |
| 17×19 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2 |
| 1 |
| 5 |
| 1 |
| 7 |
| 1 |
| 2 |
| 1 |
| 17 |
| 1 |
| 19 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 5 |
| 1 |
| 7 |
| 1 |
| 17 |
| 1 |
| 19 |
| 1 |
| 2 |
| 1 |
| 19 |
| 9 |
| 19 |
| 1 |
| 1×3 |
| 1 |
| 3×5 |
| 1 |
| 5×7 |
| 1 |
| (x-1)x |
| 1 |
| x(x+1) |
| 1 |
| (x+1)(x+2) |
| 1 |
| (x+2)(x+3) |
科目:czsx 来源: 题型:阅读理解
科目:czsx 来源: 题型:
| ||
| n个 |
科目:czsx 来源: 题型:阅读理解
| 1.310-1.39 |
| 0.3 |
| 1.310-1.39 |
| 0.3 |
科目:czsx 来源: 题型:阅读理解
| 字母 | A | B | C | D | E | F | G | H | I | J | K | L | M |
| 明码 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 字母 | N | O | P | Q | R | S | T | U | V | W | X | Y | Z |
| 明码 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 13 | 24 | 25 | 26 |
| 汉字 | 自 | 信 | |||
| 拼音 | Z | I | X | I | N |
| 明码:x | 26 | 9 | 24 | 9 | 14 |
密钥:y=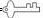 | |||||
| 密码:y | 91 | 40 | |||
| 汉字 | 自 | 信 | |||
| 拼音 | Z | I | X | I | N |
| 明码:x | 26 | 9 | 24 | 9 | 14 |
密钥:y=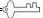 | |||||
| 密码:y | 70 | 36 | |||
科目:czsx 来源: 题型:阅读理解
先阅读下列材料,再解答后面的问题
材料:一般地,n个相同的因数![]() 相乘:
相乘:![]() 。如23=8,此时,3叫做以2为底8的对数,记为
。如23=8,此时,3叫做以2为底8的对数,记为![]() 。一般地,若
。一般地,若![]() ,则n叫做以
,则n叫做以![]() 为底b的对数,记为
为底b的对数,记为![]() ,则4叫做以3为底81的对数,记为
,则4叫做以3为底81的对数,记为![]() 。
。
问题:
1.计算以下各对数的值:log24= log216= log264=
2.观察(1)中三数4、16、64之间满足怎样的关系式?log24、log216、log264之间又满足怎样的关系式?
3.由(2)的结果,你能归纳出一个一般性的结论吗? logaM+logaN= (a>0且a≠1,M>0,N>0)
根据幂的运算法则:an·am=an+m以及对数的含义证明上述结论
科目:czsx 来源:2012届浙江省德清县士林中学中考模拟考试数学试卷(带解析) 题型:解答题
先阅读下列材料,再解答后面的问题:
要求算式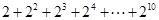 的值,我们可以按照如下方法进行:
的值,我们可以按照如下方法进行:
设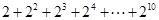 =S ① 则有2(
=S ① 则有2(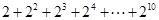 )= 2S
)= 2S
∴ 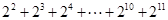 = 2S ②
= 2S ②
②-①得: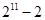 = S ∴
= S ∴ 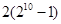 = S
= S
∴ 原式: 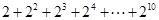 =
= 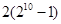
㈠ 请你根据上述方法计算: 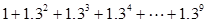 = 。
= 。
㈡ 2008年美国的金融危机引发了波及全世界的经济危机,我国也在此次经济危机中深受影响,为此2009年我国积极理性的放宽信贷,帮助我国企业、特别是中小企业度过难关,尽最大努力减少我国的失业率。 某企业在应对此次危机时积极进取,决定贷款进行技术改造,现有两种方案, 甲方案: 一次性贷款10万元,第一年便可获利1万元,以后每年获利比前一年增加30%的利润;
乙方案: 每年贷款1万元,第一年可获利1万元,以后每年获利比前一年增加5千元;
两种方案的使用期都是10年,到期一次性归还本息. 若银行两种形式的贷款都按年息5%的复利计算,
试比较两种方案中,10年的总利润,哪种获利更多? ( 结果精确到0.01 )
(取1.0510 =" 1.629" , 1.310 =" 13.786" , 1.510 =" 57.665" )
( 注意:‘复利’的计算方法,例如:一次性贷款7万元,按年息5%的复利计算;⑴若1年后归还本息,则要还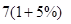 元。⑵若2年后归还本息,则要还
元。⑵若2年后归还本息,则要还 元。⑶若3年后归还本息,则要还
元。⑶若3年后归还本息,则要还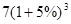 元。 )
元。 )
科目:czsx 来源:2011-2012学年广东汕头龙湖区中考模拟数学试卷(解析版) 题型:解答题
先阅读下列材料,再解答后面的问题
材料:一般地,n个相同的因数 相乘:
相乘: 。如23=8,此时,3叫做以2为底8的对数,记为
。如23=8,此时,3叫做以2为底8的对数,记为 。一般地,若
。一般地,若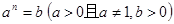 ,则n叫做以
,则n叫做以 为底b的对数,记为
为底b的对数,记为 ,则4叫做以3为底81的对数,记为
,则4叫做以3为底81的对数,记为 。
。
问题:
1.计算以下各对数的值:log24= log216= log264=
2.观察(1)中三数4、16、64之间满足怎样的关系式?log24、log216、log264之间又满足怎样的关系式?
3.由(2)的结果,你能归纳出一个一般性的结论吗? logaM+logaN= (a>0且a≠1,M>0,N>0)
根据幂的运算法则:an·am=an+m以及对数的含义证明上述结论
科目:czsx 来源: 题型:阅读理解
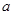 相乘:
相乘: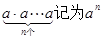 。如23=8,此时,3叫做以2为底8的对数,记为
。如23=8,此时,3叫做以2为底8的对数,记为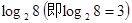 。一般地,若
。一般地,若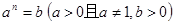 ,则n叫做以
,则n叫做以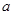 为底b的对数,记为
为底b的对数,记为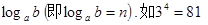 ,则4叫做以3为底81的对数,记为
,则4叫做以3为底81的对数,记为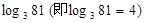 。
。科目:czsx 来源:2011-2012学年浙江省中考模拟考试数学试卷(解析版) 题型:解答题
先阅读下列材料,再解答后面的问题:
要求算式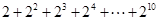 的值,我们可以按照如下方法进行:
的值,我们可以按照如下方法进行:
设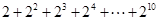 =S ① 则有2(
=S ① 则有2(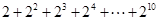 )= 2S
)= 2S
∴ 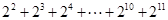 =
2S ②
=
2S ②
②-①得: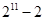 = S ∴
= S ∴ 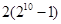 =
S
=
S
∴ 原式: 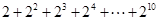 =
=
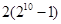
㈠ 请你根据上述方法计算: 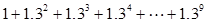 = 。
= 。
㈡ 2008年美国的金融危机引发了波及全世界的经济危机,我国也在此次经济危机中深受影响,为此2009年我国积极理性的放宽信贷,帮助我国企业、特别是中小企业度过难关,尽最大努力减少我国的失业率。 某企业在应对此次危机时积极进取,决定贷款进行技术改造,现有两种方案, 甲方案: 一次性贷款10万元,第一年便可获利1万元,以后每年获利比前一年增加30%的利润;
乙方案: 每年贷款1万元,第一年可获利1万元,以后每年获利比前一年增加5千元;
两种方案的使用期都是10年,到期一次性归还本息. 若银行两种形式的贷款都按年息5%的复利计算,
试比较两种方案中,10年的总利润,哪种获利更多? ( 结果精确到0.01 )
(取1.0510 = 1.629 , 1.310 = 13.786 , 1.510 = 57.665 )
( 注意:‘复利’的计算方法,例如:一次性贷款7万元,按年息5%的复利计算;⑴若1年后归还本息,则要还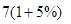 元。⑵若2年后归还本息,则要还
元。⑵若2年后归还本息,则要还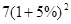 元。⑶若3年后归还本息,则要还
元。⑶若3年后归还本息,则要还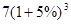 元。
)
元。
)
科目:czsx 来源:2012届广东汕头龙湖区中考模拟数学试卷(带解析) 题型:解答题
先阅读下列材料,再解答后面的问题
材料:一般地,n个相同的因数 相乘:
相乘: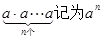 。如23=8,此时,3叫做以2为底8的对数,记为
。如23=8,此时,3叫做以2为底8的对数,记为 。一般地,若
。一般地,若 ,则n叫做以
,则n叫做以 为底b的对数,记为
为底b的对数,记为 ,则4叫做以3为底81的对数,记为
,则4叫做以3为底81的对数,记为 。
。
问题:
【小题1】计算以下各对数的值:log24= log216= log264=
【小题2】观察(1)中三数4、16、64之间满足怎样的关系式?log24、log216、log264之间又满足怎样的关系式?
【小题3】由(2)的结果,你能归纳出一个一般性的结论吗? logaM+logaN= (a>0且a≠1,M>0,N>0)
根据幂的运算法则:an·am=an+m以及对数的含义证明上述结论
科目:czsx 来源:期中题 题型:解答题
 记为an.如23=8,此时,3叫做以2为底8的对数,记log28(即log28=3).一般地,若an=b(a>01且a≠1,b>0),则n叫做a为底b的对数,记logab(即logab=n)如34=81,则4叫做以3为底81的对数,记为log381(即log381=4.问题:(1)计算以下各对数的值:
记为an.如23=8,此时,3叫做以2为底8的对数,记log28(即log28=3).一般地,若an=b(a>01且a≠1,b>0),则n叫做a为底b的对数,记logab(即logab=n)如34=81,则4叫做以3为底81的对数,记为log381(即log381=4.问题:(1)计算以下各对数的值:科目:czsx 来源:2009年辽宁省沈阳市中考数学试题 题型:044
先阅读下列材料,再解答后面的问题.
材料:密码学是一门很神秘、很有趣的学问.在密码学中,直接可以看到的信息称为明码,加密后的信息称为密码,任何密码只要找到了明码与密码的对应关系-蜜钥,就可以破译它.
密码学与数学是有关系的.为此,八年级一班数学兴趣小组经过研究实验,用所学的一次函数知识制作了一种蜜钥的编制程序.他们首先设计了一个“字母-明码对照表”:

例如:以y=3x+13为蜜钥,将“自信”二字进行加密转换后得到下表:

因此,“自”字经加密转换后的结果是“9140”.
(1)请你求出当蜜钥为y=3x+13时,“信”字经加密转换后的结果;
(2)为了提高密码的保密程度,需要频繁地更换蜜钥.若“自信”二字用新的蜜钥进行加密转换后得到下表:

请求出这个新的蜜钥,并直接写出“信”字用新的蜜钥加密转换后的结果.
科目:czsx 来源:广东省汕头市龙湖区2012年中考模拟考试数学试题 题型:044
先阅读下列材料,再解答后面的问题
材料:一般地,n个相同的因数a相乘:![]() .如23=8,此时,3叫做以2为底8的对数,记为log28(即log28=3).一般地,若an=b(b>0且a≠1,b>0),则n叫做以a为底b的对数,记为logab(即logab=n).如34=81,则4叫做以3为底81的对数,记为log381(即log381=4).
.如23=8,此时,3叫做以2为底8的对数,记为log28(即log28=3).一般地,若an=b(b>0且a≠1,b>0),则n叫做以a为底b的对数,记为logab(即logab=n).如34=81,则4叫做以3为底81的对数,记为log381(即log381=4).
问题:(1)计算以下各对数的值:log24=________log216=________log264=________.
(2)观察(1)中三数4、16、64之间满足怎样的关系式?log24、log216、log264之间又满足怎样的关系式?
(3)由(2)的结果,你能归纳出一个一般性的结论吗?
logaM+logaN=________.(a>0且a≠1,M>0,N>0)
根据幂的运算法则:an·am=an+m以及对数的含义证明上述结论.
科目:czsx 来源: 题型:解答题
科目:czsx 来源: 题型:阅读理解
先阅读下列材料,再解答后面的问题.
材料:密码学是一门很神秘、很有趣的学问,在密码学中,直接可以看到的信息称为明码,加密后的信息称为密码,任何密码只要找到了明码与密码的对应关系――密钥,就可以破译它.
密码学与数学是有关系的.为此,八年一班数学兴趣小组经过研究实验,用所学的一次函数知识制作了一种密钥的编制程序.他们首先设计了一个“字母――明码对照表”:
| 字母 | A | B | C | D | E | F | G | H | I | J | K | L | M |
| 明码 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 字母 | N | O | P | Q | R | S | T | U | V | W | X | Y | Z |
| 明码 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 |
例如,以y=3x+13为密钥,将“自信”二字进行加密转换后得到下表:
| 汉 字 | 自 | 信 | |||
| 拼 音 | Z | I | X | I | N |
| 明码:x | 26 | 9 | 24 | 9 | 14 |
|
| |||||
| 密码:y | 91 | 40 | |||
因此,“自”字加密转换后的结果是“9140”.
问题:
(1)请你求出当密钥为y=3x+13 时,“信”字经加密转换后的结果;
(2)为了提高密码的保密程度,需要频繁地更换密钥.若“自信” 二字用新的密钥加密转换后得到下表:
| 汉 字 | 自 | 信 | ||||
| 拼 音 | Z | I | X | I | N | |
| 明码:x | 26 | 9 | 24 | 9 | 14 | |
|
| ||||||
| 密码:y | 70 | 36 | ||||
请求出这个新的密钥,并直接写出“信”字用新的密钥加密转换后的结果.
科目:czsx 来源:学习周报 数学 华师大八年级版2009-2010年 第3期 总第159期 华师大版 题型:044
先阅读下列材料,再解答后面的问题
材料:一般地,n个相同的因数a相乘:![]() ,记为an.如2×2×2=23=8.一般地,若an=b(a>0且a≠1,b>0),则n叫做以a为底b的对数,记为logab(即logab=n).如34=81,则4叫做以3为底81的对数,记为log381(即log381=4).
,记为an.如2×2×2=23=8.一般地,若an=b(a>0且a≠1,b>0),则n叫做以a为底b的对数,记为logab(即logab=n).如34=81,则4叫做以3为底81的对数,记为log381(即log381=4).
问题:(1)计算以下各对数的值:
log24=________,log216=________,log264=________;
(2)观察(1)中的三个数4、16、64之间满足怎样的关系式?log24、log216、log264之间又满足怎样的关系式?
(3)由(2)的结果,你能归纳出一个一般性的结论吗?
logaM+logaN=________(a>0且a≠1,M>0,N>0).
根据幂的运算法则:an·am=an+m以及对数的含义,说明上述结论成立的理由.