精英家教网 >
试题搜索列表 >抛物线 与x轴的正半轴交于点A、B两点,与y轴交于点C,且线段AB的长为1,△ABC的面积为1,则b的值为 .
抛物线 与x轴的正半轴交于点A、B两点,与y轴交于点C,且线段AB的长为1,△ABC的面积为1,则b的值为 .答案解析
科目:czsx
来源:
题型:
已知:正方形OABC的边OC、OA分别在x、y轴的正半轴上,设点B(4,4),点P(t,0)是x轴上一动点,过点O作OH⊥AP于点H,直线OH交直线BC于点D,连AD.
(1)如图1,当点P在线段OC上时,求证:OP=CD;
(2)在点P运动过程中,△AOP与以A、B、D为顶点的三角形相似时,求t的值;
(3)如图2,抛物线y=-
x
2+
x+4上是否存在点Q,使得以P、D、Q、C为顶点的四边形为平行四边形?若存在,请求出t的值;若不存在,请说明理由.
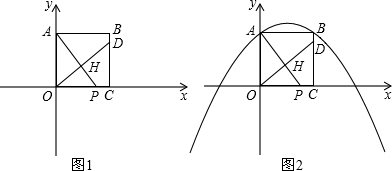
查看答案和解析>>
科目:czsx
来源:
题型:
已知:在如图1所示的平面直角坐标系xOy中,A,C两点的坐标分别为A(2,3),C(n,-3)(其中n>0),点B在x轴的正半轴上.动点P从点O出发,在四边形OABC的边上依次沿O-A-B-C的顺序向点C移动,当点P与点C重合时停止运动.设点P移动的路径的长为l,△POC的面积为S,S与l的函数关系的图象如图2所示,其中四边形ODEF是等腰梯形.
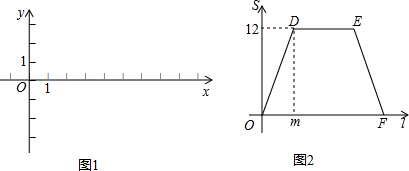
(1)结合以上信息及图2填空:图2中的m=
;
(2)求B,C两点的坐标及图2中OF的长;
(3)在图1中,当动点P恰为经过O,B两点的抛物线W的顶点时,
①求此抛物线W的解析式;
②若点Q在直线y=-1上方的抛物线W上,坐标平面内另有一点R,满足以B,P,Q,R四点为顶点的四边形是菱形,求点Q的坐标.
查看答案和解析>>
科目:czsx
来源:
题型:
已知抛物线y=-x2+2(k-1)x+k+2与x轴交于A、B两点,且点A在x轴的负半轴上,点B在x轴的正半轴上.
(1)求实数k的取值范围;
(2)设OA、OB的长分别为a、b,且a:b=1:5,求抛物线的解析式;
(3)在(2)的条件下,以AB为直径的⊙D与y轴的正半轴交于P点,过P点作⊙D的切线交x轴于E点,求点E的坐标.
查看答案和解析>>
科目:czsx
来源:
题型:
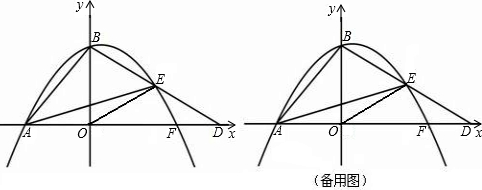
如图,在平面直角坐标系xOy中,点B的坐标为(0,2),点D在x轴的正半轴上,∠ODB=30°,OE为△BOD的中线,过B、E两点的抛物线
y=ax2+x+c与x轴相交于A、F两点(A在F的左侧).
(1)求抛物线的解析式;
(2)等边△OMN的顶点M、N在线段AE上,求AE及AM的长;
(3)点P为△ABO内的一个动点,设m=PA+PB+PO,请直接写出m的最小值,以及m取得最小值时,线段AP的长.
查看答案和解析>>
科目:czsx
来源:
题型:
已知抛物线y=-
(x+2)
2+k与x轴交于A、B两点,与y轴交于点C,其中点B在x轴的正半轴上,C点在y轴的正半轴上,线段OB、OC的长(OB<OC)是方程x
2-10x+16=0的两个根.
(1)求A、B、C三点的坐标;
(2)在平面直角坐标系内画出抛物线的大致图象并标明顶点坐标;
(3)连AC、BC,若点E是线段AB上的一个动点(与A、B不重合),过E作EF∥AC交BC于F,连CE,设AE=m,△CEF的面积为S,求S与m的函数关系式,并写出自变量m的取值范围;
(4)在(3)的基础上说明S是否存在最大值,并求出此时点E的坐标,判断此时△BCE的形状;若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
如图1,抛物线y=ax
2-2ax-b(a<0)与x轴的一个交点为B(-1,0),与y轴的正半轴交于点C,顶点为D.
(1)求顶点D的坐标(用含a的代数式表示);
(2)若以AD为直径的圆经过点C.
①求抛物线的解析式;
②如图2,点E是y轴负半轴上的一点,连接BE,将△OBE绕平面内某一点旋转180°,得到△PMN(点P、M、N分别和点O、B、E对应),并且点M、N都在抛物线上,作MF⊥x轴于点F,若线段MF:BF=1:2,求点M、N的坐标;
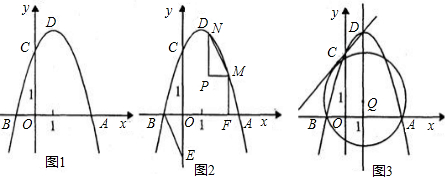
③如图3,点Q在抛物线的对称轴上,以Q为圆心的圆过A、B两点,并且和直线CD相切,求点Q的坐标.
查看答案和解析>>
科目:czsx
来源:
题型:

探索研究
已知如图,过O且半径为5的⊙P交x的正半轴于点M(2m,0)、交y轴的负半轴于点D,弧OBM与⊙P的弧OAM关于x轴对称,其中A、B、C是过点P且垂直于x轴的直线与两弧及圆的交点.点A到x轴的距离为h,以B为顶点且过D的抛物线交⊙P于点E.
(1)填空:B的坐标为
(m,-h)
(m,-h)
,C的坐标为
(m,h-10)
(m,h-10)
,D的坐标为
(0,2h-10)
(0,2h-10)
;(可含m、h)
(2)当m=4时,
①求此抛物线的函数关系式并写出点E的坐标;
②点Q在y轴上,且S
△CEQ=S
△CEP,求Q点坐标.
(3)是否存在实数m,使得以B、C、D、E为顶点的四边形组成菱形?若存在,求m的值;若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
如图,在直角坐标系中,点A的坐标为(-2
,0),⊙P刚好与x轴相切于点A,⊙P交y的正半轴于
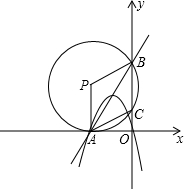
点B,点C,且BC=4.
(1)求半径PA的长;
(2)求证:四边形CAPB为菱形;
(3)有一开口向下的抛物线过O,A两点,当它的顶点不在直线AB的上方时,求函数表达式的二次项系数a的取值范围.
查看答案和解析>>
科目:czsx
来源:
题型:
已知抛物线y=x
2-(2m-1)x+4m-6.
(1)试说明对于每一个实数m,抛物线都经过x轴上的一个定点;
(2)设抛物线与x轴的两个交点A(x
1,0)和B(x
2,0)(x
1<x
2)分别在原点的两侧,且A、B两点间的距离小于6,求m的取值范围;
(3)抛物线的对称轴与x轴交于点C
(,0),在(2)的条件下,试判断是否存在m的值,使经过点C及抛物线与x轴的一个交点的⊙M与y轴的正半轴相切于点D,且被x轴截得的劣弧与
是等弧?若存在,求出所有满足条件的m的值;若不存在,说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:

(2012•泰安)如图,半径为2的⊙C与x轴的正半轴交于点A,与y轴的正半轴交于点B,点C的坐标为(1,0).若抛物线y=-
x
2+bx+c过A、B两点.
(1)求抛物线的解析式;
(2)在抛物线上是否存在点P,使得∠PBO=∠POB?若存在,求出点P的坐标;若不存在说明理由;
(3)若点M是抛物线(在第一象限内的部分)上一点,△MAB的面积为S,求S的最大(小)值.
查看答案和解析>>
科目:czsx
来源:
题型:
如图,⊙M是以点M(4,0)为圆心,5个单位长度为半径的圆.⊙M与x轴交于点A、B(A在B的左侧
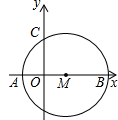
),⊙M与y轴的正半轴交于点C.
求:(1)点A、B、C的坐标;
(2)经过点A、B、C三点的抛物线的解析式.
查看答案和解析>>
科目:czsx
来源:
题型:
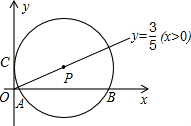
如图,P是射线y=
x上的一动点,以P为圆心的⊙P与y轴相切于C点,与x轴的正半轴交于A、B两点.
(1)若⊙P的半径为5,求点P、A的坐标;
(2)在(1)的条件下,求以点P为顶点,且经过A点的抛物线的解析式;并判定该抛物线是否经过点C关于原点的对称点D,说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:

已知:抛物线y=ax
2+bx+6与x轴交于A(1,0),B(3,0).
(1)试确定抛物线的解析式及其顶点C的坐标;
(2)设抛物线的对称轴与x轴的交点为D,y的正半轴上有一动点P,当△POA∽△ADC时,试确定P点的坐标.
查看答案和解析>>
科目:czsx
来源:
题型:

已知抛物线y=
-x
2+bx+4上有不同的两点E(k+3,0)和F(-k-1,0).
(1)求抛物线的解析式.
(2)如图,抛物线y=
-x
2+bx+4与x轴和y轴的正半轴分别交于点A和B,M为AB的中点,∠PMQ在AB的同侧以M为中心旋转,且∠PMQ=45°,MP交y轴于点C,MQ交x轴于点D.设AD的长为m(m>0),BC的长为n,求n和m之间的函数关系式.
(3)当k>0且∠PMQ的边过点F时,求m、n的值.
查看答案和解析>>
科目:czsx
来源:
题型:
如图,在直角坐标系中,O为原点,抛物线y=x
2+bx+3与x轴的负半轴交于点A,与y轴的正半轴交于
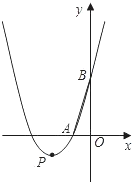
点B,tan∠ABO=
,顶点为P.
(1)求抛物线的解析式;
(2)若抛物线向上或向下平移|k|个单位长度后经过点C(-5,6),试求k的值及平移后抛物线的最小值;
(3)设平移后的抛物线与y轴相交于D,顶点为Q,点M是平移的抛物线上的一个动点.请探究:当点M在何位置时,△MBD的面积是△MPQ面积的2倍求出此时点M的坐标.友情提示:抛物线y=ax
2+bx+c(a≠0)的对称轴是
x=-,顶点坐标是
(-,).
查看答案和解析>>
科目:czsx
来源:
题型:
(2012•樊城区模拟)如图,点O是坐标原点,四边形ABCO是菱形,点A的坐标为(-3,4),点C在x轴的正半
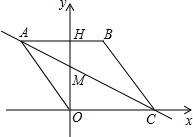
轴上,直线AC交y轴于点M,AB边交y轴于点H.
(1)求B、C两点坐标;
(2)抛物线y=
x
2-bx+c经过A、O两点,求抛物线的解析式,并验证点C是否在抛物线上;
(3)在x轴上是否存在一点P,使△PCM与△ABC相似?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
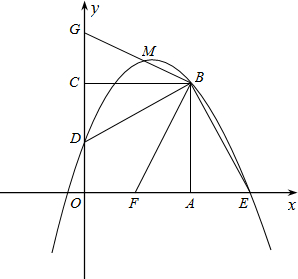
(2012•德阳)在平面直角坐标xOy中,(如图)正方形OABC的边长为4,边OA在x轴的正半轴上,边OC在y轴的正半轴上,点D是OC的中点,BE⊥DB交x轴于点E.
(1)求经过点D、B、E的抛物线的解析式;
(2)将∠DBE绕点B旋转一定的角度后,边BE交线段OA于点F,边BD交y轴于点G,交(1)中的抛物线于M(不与点B重合),如果点M的横坐标为
,那么结论OF=
DG能成立吗?请说明理由;
(3)过(2)中的点F的直线交射线CB于点P,交(1)中的抛物线在第一象限的部分于点Q,且使△PFE为等腰三角形,求Q点的坐标.
查看答案和解析>>
科目:czsx
来源:
题型:
在直角坐标系中,O为坐标原点,点A的坐标为(2,2),点C是线段OA上的一个动点(不运动至O,A两点),过点C作CD⊥x轴,垂足为D,以CD为边作如图所示的正方形CDEF.连接AF并延长交x轴的正半轴于点B,连接OF.
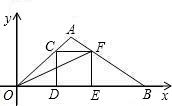
(1)猜想OD和DE之间的数量关系,并说明理由;
(2)设OD=t,求OB的长(用含t的代数式表示);
(3)若点B在E的右侧时,△BFE与△OFE能否相似?若能,请你求出此时经过O,A,B三点的抛物线解析式;若不能,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
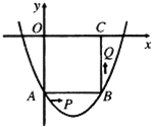
如图在平面直角坐标系xoy中,正方形OABC的边长为2厘米,点A、C分别在y轴的负半轴和x轴的正半轴上.抛物线y=ax
2+bx+c经过点A,B和点D(4,
)
(1)求抛物线的解析式;
(2)如果点P由点A开始沿AB边以2厘米/秒的速度向点B移动,同时点Q由B点开始沿BC边以1厘米/秒的速度向点C移动.若P、Q中有一点到达终点,则另一点也停止运动,设P、Q两点移动的时间为t秒,S=PQ
2(厘米
2)写出S与t之间的函数关系式,并写出t的取值范围,当t为何值时,S最小;
(3)当s取最小值时,在抛物线上是否存在点R,使得以P、B、Q、R为顶点的四边形是平行四边形?如果存在,求出点R的坐标;如果不存在,请说明理由.
(4)在抛物线的对称轴上求出点M,使得M到D,A距离之差最大?写出点M的坐标.
查看答案和解析>>
科目:czsx
来源:
题型:
已知抛物线y=-x2+(m-2)x+3(m+1)交x轴于A(x1,0),B(x2,0),交y轴的正半轴于C点,且x1<x2,|x1|>|x2|,OA2+OB2=2OC+1.
(1)求抛物线的解析式;
(2)是否存在与抛物线只有一个公共点C的直线.如果存在,求符合条件的直线的表达式;如果不存在,请说明理由.
查看答案和解析>>

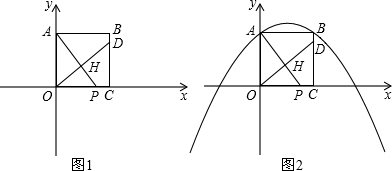
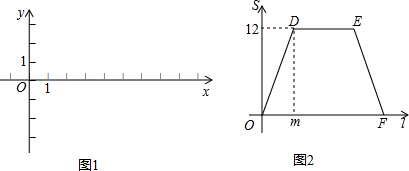


 探索研究
探索研究 点B,点C,且BC=4.
点B,点C,且BC=4.
 (2012•泰安)如图,半径为2的⊙C与x轴的正半轴交于点A,与y轴的正半轴交于点B,点C的坐标为(1,0).若抛物线y=-
(2012•泰安)如图,半径为2的⊙C与x轴的正半轴交于点A,与y轴的正半轴交于点B,点C的坐标为(1,0).若抛物线y=- ),⊙M与y轴的正半轴交于点C.
),⊙M与y轴的正半轴交于点C. 如图,P是射线y=
如图,P是射线y= 已知:抛物线y=ax2+bx+6与x轴交于A(1,0),B(3,0).
已知:抛物线y=ax2+bx+6与x轴交于A(1,0),B(3,0). 已知抛物线y=-
已知抛物线y=- 点B,tan∠ABO=
点B,tan∠ABO= 轴上,直线AC交y轴于点M,AB边交y轴于点H.
轴上,直线AC交y轴于点M,AB边交y轴于点H.
 (1)猜想OD和DE之间的数量关系,并说明理由;
(1)猜想OD和DE之间的数量关系,并说明理由; 如图在平面直角坐标系xoy中,正方形OABC的边长为2厘米,点A、C分别在y轴的负半轴和x轴的正半轴上.抛物线y=ax2+bx+c经过点A,B和点D(4,
如图在平面直角坐标系xoy中,正方形OABC的边长为2厘米,点A、C分别在y轴的负半轴和x轴的正半轴上.抛物线y=ax2+bx+c经过点A,B和点D(4,