练习册

  • 练习册
  • 试题
    精英家教网 > 试题搜索列表 >在梯形ABCD中，AD//BC,AC,BD,交于O点，S△AOD：S△COB=1:9

    在梯形ABCD中，AD//BC,AC,BD,交于O点，S△AOD：S△COB=1:9答案解析

    科目：czsx 来源： 题型：013

    在梯形ABCD中，AD∥BC.AC,BD相交于O ,如果AD：BC=1：3, 那么下列结论正确的是（　　 ）

    A．S△COD =9 S△AOD B．S△ABC =9 S△ACD C．S△BOC =9 S△AOD D．S△DBC =9 S△AOD

    查看答案和解析>>

    科目：czsx 来源：数学教研室 题型：013

    在梯形ABCD中，AD∥BC.AC,BD相交于O,如果AD：BC=1：3, 那么下列结论正确的是（  ）

    A, S△COD =9 S△AOD    B, S△ABC =9 S△ACD   C,  S△BOC =9 S△AOD  D, S△DBC =9 S△AOD

     

    查看答案和解析>>

    科目：czsx 来源： 题型：

    如图，在梯形ABCD中，AD∥BC，AB=DC，过点D作DE⊥BC，垂足为E，并延长DE至F，使EF=DE．连接BF、CF、AC．
    （1）求证：四边形ABFC是平行四边形；
    （2）如果DE=6，EC=4，BE=9 求证四边形ABFC是矩形．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    如图，在梯形ABCD中，AD∥BC，AB=DC，过点D作DE⊥BC，垂足为E，并延长DE至F，使EF=DE．连接BF、CF、AC．求证：四边形ABFC是平行四边形．

    查看答案和解析>>

    科目：czsx 来源： 题型：

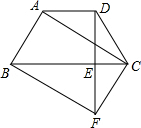    精英家教网如图，在梯形ABCD中，AD∥BC，AB=DC，过点D作DE⊥BC，垂足为E，并延长DE至F，使EF=DE．连接BF、CF、AC．
    （1）求证：四边形ABFC是平行四边形；
    （2）如果DE2=BE•CE，求证：四边形ABFC是矩形．

    查看答案和解析>>

    科目：czsx 来源： 题型：

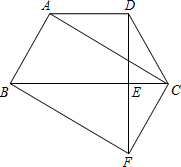    （2012•开平区二模）如图，在梯形ABCD中，AD∥BC，AB=DC，过点D作DE⊥BC，垂足为E，并延长DE至F，使EF=DE．连接BF、CF、AC．
    （1）求证：四边形ABFC是平行四边形；
    （2）若四边形ABFC是矩形，求证：△BED∽△DEC；
    （3）在（2）的条件下，若等腰梯形的腰AB=5cm，下底BC=8cm，点P是BC边上的一个动点，以点P为圆心，以1cm长为半径的圆从点B出发，以每秒2cm的速度向点C移动（不与点C重合），当⊙P与AC边相切时，求⊙P移动的时间．

    查看答案和解析>>

    科目：czsx 来源：2012年福建省漳州市中考数学模拟试卷（三）（解析版） 题型：解答题

    如图，在梯形ABCD中，AD∥BC，AB=DC，过点D作DE⊥BC，垂足为E，并延长DE至F，使EF=DE．连接BF、CF、AC．
    （1）求证：四边形ABFC是平行四边形；
    （2）如果DE2=BE•CE，求证：四边形ABFC是矩形．

    查看答案和解析>>

    科目：czsx 来源：2011-2012学年江苏省镇江市扬中市九年级（上）期中数学试卷（解析版） 题型：解答题

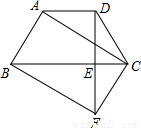    如图，在梯形ABCD中，AD∥BC，AB=DC，过点D作DE⊥BC，垂足为E，并延长DE至F，使EF=DE．连接BF、CF、AC．
    （1）求证：四边形ABFC是平行四边形；
    （2）如果DE2=BE•CE，求证：四边形ABFC是矩形．

    查看答案和解析>>

    科目：czsx 来源：2011年上海市中考数学试卷（解析版） 题型：解答题

    如图，在梯形ABCD中，AD∥BC，AB=DC，过点D作DE⊥BC，垂足为E，并延长DE至F，使EF=DE．连接BF、CF、AC．
    （1）求证：四边形ABFC是平行四边形；
    （2）如果DE2=BE•CE，求证：四边形ABFC是矩形．

    查看答案和解析>>

    科目：czsx 来源： 题型：解答题

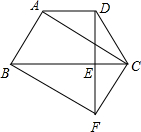    作业宝如图，在梯形ABCD中，AD∥BC，AB=DC，过点D作DE⊥BC，垂足为E，并延长DE至F，使EF=DE．连接BF、CF、AC．
    （1）求证：四边形ABFC是平行四边形；
    （2）如果DE=6，EC=4，BE=9 求证四边形ABFC是矩形．

    查看答案和解析>>

    科目：czsx 来源：2011-2012学年四川省巴中市通江县铁佛中学九年级（上）第三次联考数学试卷（解析版） 题型：解答题

    如图，在梯形ABCD中，AD∥BC，AB=DC，过点D作DE⊥BC，垂足为E，并延长DE至F，使EF=DE．连接BF、CF、AC．求证：四边形ABFC是平行四边形．

    查看答案和解析>>

    科目：czsx 来源：2012年山东省聊城市东昌中学中考数学二模试卷（解析版） 题型：解答题

    如图，在梯形ABCD中，AD∥BC，AB=DC，过点D作DE⊥BC，垂足为E，并延长DE至F，使EF=DE．连接BF、CF、AC．
    （1）求证：四边形ABFC是平行四边形；
    （2）如果DE2=BE•CE，求证：四边形ABFC是矩形．

    查看答案和解析>>

    科目：czsx 来源：2012年广东省广州市广雅中学中考数学一模试卷（解析版） 题型：解答题

    如图，在梯形ABCD中，AD∥BC，AB=DC，过点D作DE⊥BC，垂足为E，并延长DE至F，使EF=DE．连接BF、CF、AC．
    （1）求证：四边形ABFC是平行四边形；
    （2）如果DE2=BE•CE，求证：四边形ABFC是矩形．

    查看答案和解析>>

    科目：czsx 来源：2011-2012学年江苏省淮安市新区实验学校九年级（上）第一次调研数学试卷（解析版） 题型：解答题

    如图，在梯形ABCD中，AD∥BC，AB=DC，过点D作DE⊥BC，垂足为E，并延长DE至F，使EF=DE．连接BF、CF、AC．
    （1）求证：四边形ABFC是平行四边形；
    （2）如果DE2=BE•CE，求证：四边形ABFC是矩形．

    查看答案和解析>>

    科目：czsx 来源：2013年上海市中考数学模拟试卷（六）（解析版） 题型：解答题

    如图，在梯形ABCD中，AD∥BC，AB=DC，过点D作DE⊥BC，垂足为E，并延长DE至F，使EF=DE．连接BF、CF、AC．
    （1）求证：四边形ABFC是平行四边形；
    （2）如果DE2=BE•CE，求证：四边形ABFC是矩形．

    查看答案和解析>>

    科目：czsx 来源：2012-2013学年内蒙古鄂尔多斯市大兴中学九年级（上）月考数学试卷（10月份）（解析版） 题型：解答题

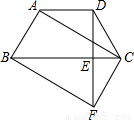
    如图，在梯形ABCD中，AD∥BC，AB=DC，过点D作DE⊥BC，垂足为E，并延长DE至F，使EF=DE．连接BF、CF、AC．求证：四边形ABFC是平行四边形．

    查看答案和解析>>

    科目：czsx 来源：上海中考真题 题型：证明题

    如图，在梯形ABCD中，AD//BC，AB=DC，过点D作DE⊥BC，垂足为E，并延长DE至F，使EF=DE，联结BF、CD、AC。
    （1）求证：四边形ABFC是平行四边形；
    （2）如果DE2=BE·CE，求证四边形ABFC是矩形。

    查看答案和解析>>

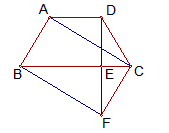
    科目：czsx 来源：2012年河北省唐山市开平区中考数学二模试卷（解析版） 题型：解答题

    如图，在梯形ABCD中，AD∥BC，AB=DC，过点D作DE⊥BC，垂足为E，并延长DE至F，使EF=DE．连接BF、CF、AC．
    （1）求证：四边形ABFC是平行四边形；
    （2）若四边形ABFC是矩形，求证：△BED∽△DEC；
    （3）在（2）的条件下，若等腰梯形的腰AB=5cm，下底BC=8cm，点P是BC边上的一个动点，以点P为圆心，以1cm长为半径的圆从点B出发，以每秒2cm的速度向点C移动（不与点C重合），当⊙P与AC边相切时，求⊙P移动的时间．

    查看答案和解析>>

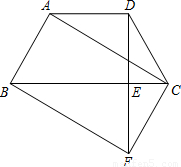
    科目：czsx 来源：2013年广东省广州六中中考数学一模试卷（解析版） 题型：解答题

    如图，在梯形ABCD中，AD∥BC，AB=DC，过点D作DE⊥BC，垂足为E，并延长DE至F，使EF=DE．连接BF、CF、AC．
    （1）求证：四边形ABFC是平行四边形；
    （2）如果DE2=BE•CE，求证：四边形ABFC是矩形．

    查看答案和解析>>

    科目：czsx 来源：数学课外练习八年级下学期使用 题型：059

    如图，在梯形ABCD中，AD∥BC，AB＝DC，点P是BC边上一点，PE⊥AB于E，PF⊥DC于F，BG⊥DC于G．求证：PE＋PF＝BG．

    想一想：如果条件中的“梯形ABCD中，AD∥BC，AB＝DC”变为“△ABC中，AB＝AC”，其他条件不变，这个结论还成立吗？若成立，予以证明．

    查看答案和解析>>